題主所提到與運動方向同向的光速問題還真就不能直接回答,咱們必須換一個角度,先研究一下光與運動方向垂直時的情況。隨著一步一步遞推下來,水到渠成,問題就迎刃而解了。(放心,我只用了一點簡單的代數,上過中學的人都應該看得懂)
那麽先想象這樣一個場景:
【思想實驗一】 [1]
觀察者B站在地面上。頭頂有一艘飛船,以速度v [2] ,在平行於地面的方向上,勻速向右飛行。飛船上安裝了一台光子鐘,儀器的下端有發射器向上發射光子,儀器上端則裝有鏡面,光子被鏡面反射向下,回到下端初始位置時由探測器接收。此鐘可測出光子從發射到返回所經過的時長。太空人A在飛船上記錄光子鐘的讀數。對他而言,光子是在垂直的方向上做往返運動,光子的發射與接收發生在 同一位置 。
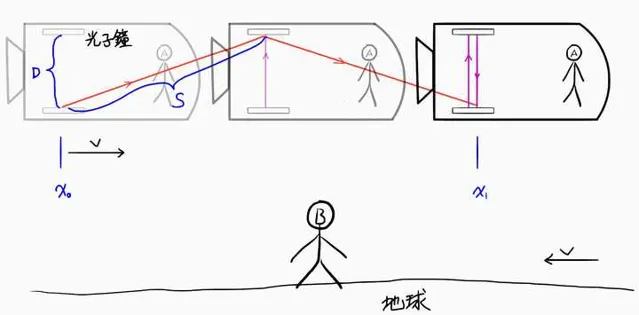
由於飛船相對於地面有一個水平方向的速度v,那麽對地面的觀察者B而言(假定他也能看到飛船中的一切),飛船上光子鐘裏光子所走的路線則是斜上斜下的「人」字形,光子的發射和接收發生在水平方向一左一右 兩個不同的位置 上 。
設光子鐘上下兩端的間距為D,觀察者A所觀測到的光子的往返路程為2D,時長為τ;地面觀察者B所觀測的光子上行和下行路徑長度同為S,光子往返的總路程為2S,時長為t。
速度= 距離/時間
兩個觀察者都可以根據自己測得的時間和距離算出光速,那麽 光速不變 即意味著
\frac{2D}{\tau} = \frac{2S}{t} = c
即 * 距離與時長的比值不變 *!
飛船相對於地面的速度 v 是明確的,那麽從光子的發射到接收,飛船在水平方向上所透過的距離對地面觀察者B而言就等於 vt。令 2L=vt ,我們即可得出如下圖所示的兩個全等直角三角形。
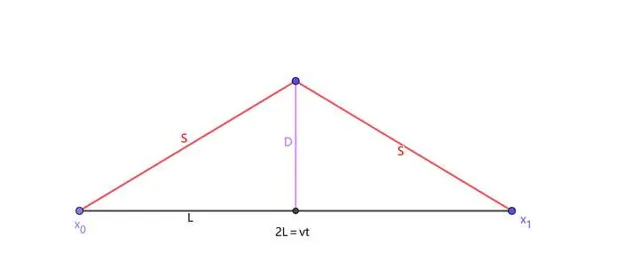
根據畢達哥拉斯定理(勾股定理), S^2 = D^2 + L^2 ,若將A、B二人所記錄的時長、距離以及不變的光速c代入,即可得:
\begin{align} S^2 =& D^2 +L^2\\ (ct)^2 =& (c\tau)^2 + (vt)^2\\ c^2t^2 =& c^2\tau^2+v^2t^2\\ (c^2 -v^2)t^2 =& c^2\tau^2\\ t^2 =& \frac{c^2}{c^2-v^2}\tau^2\\ \color{red}{t} = &\frac{1}{\sqrt{1-(v/c)^2}}\color{violet}{\tau} \end{align}
τ 前面的這個系數 \frac{1}{\sqrt{1 - v^2/c^2}} 就叫做 勞侖茲因子 ,記作 γ 。也就是說,B所記錄的光子的往返時長 t 跟A所記錄的時長 τ 是不一樣的。如果你把A、B兩者的相對速度 v 代入,假令 v = 0.5c,會發現 γ = 1.1547 > 1。 \because v <c ,\therefore \gamma > 1 。
同樣的兩個事件的間隔(光子的發射和接收)在B參照系裏的耗時比A參照系裏的長,或者反過來說,A的時鐘比B的時鐘走得慢——這就是「 時間膨脹 」。
於是你要問了。既然速度 v 是相對的,對地球上的 B 而言,飛船上的時鐘變慢了,對飛船上的A而言地球上的時鐘是不是也變慢了呢?—— 確實如此 。所以我們必須回過頭來留意一下前文中加了黑體的條件:對飛船上的 A 而言,兩個事件是發生在同一位置的。因此,他所測得的時間就叫作 原時 (或曰原時間 proper time)。而對地面上的 B 而言,兩事件發生在不同位置,那麽他所測得的時間就是 γτ 。當然,如果把實驗顛倒過來,把光子鐘放在地面上,地面上測得的時間就成了原時了。
速度總是相對的, A 相對於 B 的速度是 v, 那麽 B 相對於 A 的速度也必然是 v,於是問題來了。回看一下上圖的三角形,光子的往返過程中,飛船相對於B向右橫向移動了 2L 的距離。B觀察到,光子鐘收發點的水平位置從 x_0 移動到了 x_1 。既然 v_A = v_B ,那不就意味著 \frac{2L}{t} = v = \frac{?}{\tau} 嘛!對飛船上的A而言,地面相對於他自己是在向左移動。難道在光子往返的 τ 時間內,地面移動的距離竟然不是2L?沒錯! 將勞侖茲因子代入,
\begin{align} \frac{2L}{t} =& \frac{2L'}{\tau}\\ \frac{2L}{\gamma \tau} =& \frac{2L'}{\tau}\\ L' =& \frac{1}{\gamma}L \end{align}
對地面上的B而言, x_0 和 x_1 兩個點(位置)是靜止的,我們把相對於觀察者靜止的兩點間的距離稱作 原長度 (或曰固有長度 proper length),通常記作 L_0 。而相對兩個點運動的觀察者所測得的兩點間的距離(如前面式子中的L')則是原長度的1/γ 倍(恒< 1)。也就是說,飛船裏A所量得的水平方向上相對其運動的長度(比如飛船的飛行路程)是短於地面上B所量得的靜止長度的,我們把這個現象就叫做「 長度收縮 」。
還有一個問題,那就是與運動方向垂直的長度。就比方說這個光子鐘的上下兩端的間距,會不會對A、B而言也不一樣呢?倘若D_A \neq D_B ,以上的一連串推導就都不成立了。看下圖:
【思想實驗二】
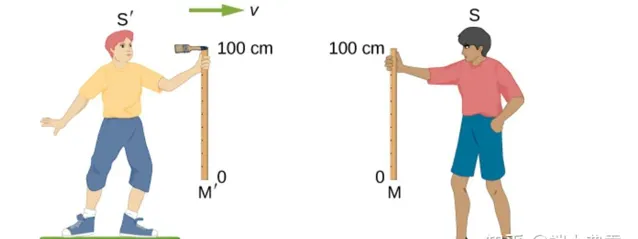
兩男孩(S' 和 S)各拿一把靜止時長度為1米的直尺,垂直舉起。男孩S'的尺子上端固定了一個蘸了墨的毛刷。S在地面站定,而S'以極高的速度 v 向著與S稍稍錯開一點的方向滑行過來。當兩者擦肩而過時,兩人尺子的下端距地高度相同,尺間的距離也是毛刷能夠得到的。如果事後S檢查自己的尺子M,發現上端下面一點有一道墨跡,就說明,S'的尺子M' 比自己尺子M短。然而速度是相對的。對S'而言,自己才是靜止的,是 S 以速度v迎面而來,如果以高速 v 運動會使豎直方向的尺子變短的化,在兩人交會的一剎那,S'會看到自己尺子上的毛刷在對方尺頭上空劃過。事後檢查,S的M尺上應該沒有墨跡。毛刷在尺子上畫出墨跡這件事怎麽能既發生又不發生呢?這明顯是個悖論。所以說,垂直於運動方向的兩把尺子必定是等長的,即 D_A = D_B 。
Okay, 終於可以討論「追光」的問題了。還是一開始設定的那個場景,只不過,這回飛船上的光子鐘橫過來裝。讓光子鐘收發和反射兩端的間距正好等於飛船的長度。如下圖:
【思想實驗三】
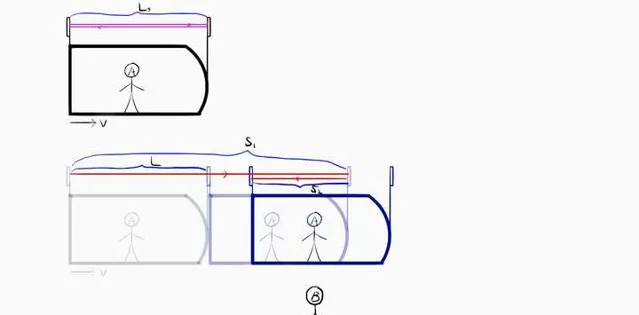
飛船上的A量得的飛船長度是 L_0 ,因為A相對於飛船的兩端靜止,所以這個長度就是原長度。又對A而言,光子的發射接收發生在同處,所以他測得的時長 τ 也就是原時。於是他的光路方程式就是 2L_0 = c\tau 。(圖示的上半部份)
地面上的B量得的飛船長度是L。他所觀測到的光子的路徑 S 由前進階段的 S_1 和返回階段的 S_2 兩段組成。(圖示下半部份)
我們需要先搞清楚 S_1、S_2 跟船體長度 L 的關系。先假定光子走完 S_1 所經過的時間為 t_1 , S_2 所對應的則為 t_2 。那麽
S_1 = ct_1 = L + vt_1 \implies L = (c-v)t_1 ,進而知 \frac{S_1}{L} = \frac{c\cancel{t_1}}{(c-v)\cancel{t_1}} 。同理, S_2 = ct_2 = L - vt_2 \implies L = (c+v)t_2 \implies \frac{S_2}{L} =\frac{c}{c+v} 。於是 \frac{S}{2L}=\frac{S_1 +S_2}{2L} = \frac{c^2}{c^2-v^2} =\frac{1}{1-(v/c)^2} 。
又由於長度收縮, L = \frac{L_0}{\gamma} \implies S = \frac{S}{2L}\cdot \frac{2L_0}{\gamma}= \frac{1}{1-(v/c)^2}\cdot\sqrt{1-(v/c)^2}\cdot L_0 = \gamma \cdot 2L_0
也就是說,地面所觀察到的光子路程是飛船上所觀察到的γ倍。
又由於時間膨脹,地面觀測到的光子往返時間 t = \gamma \tau 。
\frac{S}{t} = \frac{\cancel{ \gamma} \cdot 2L_0}{\cancel{\gamma} \tau} = c
——理解了沒?
參考
- ^ 本文所舉之「實驗一」「實驗二」,以及對「時間膨脹」「長度收縮」的解釋均取材於Rice大學的Openstax教材【University Physics Volume III】 https://openstax.org/details/books/university-physics-volume-3
- ^ 本文所言的「速度」嚴格來講,所指都是「速率」(speed),而非向量的「速度」(velocity)。光速不變的速,指的就是speed。我之所以選用這種含混的說法,是因為我覺得漢語的「速率」一詞太拗口。











