聲子頻率與溫度有關
但是這種關系很復雜,不能直接的描述為溫度的函數形式。
之前借用分子動力學軟件計算了某種金屬的聲子態密度的一個小練習(勢函數采用的是經驗勢)。方法是從MD模擬中得到速度自關聯函數,然後傅立葉變換就得到聲子DOS。
這裏面我沒有去算某個模的頻率,我也算不了。但是可以從態密度裏面看出一些東西。
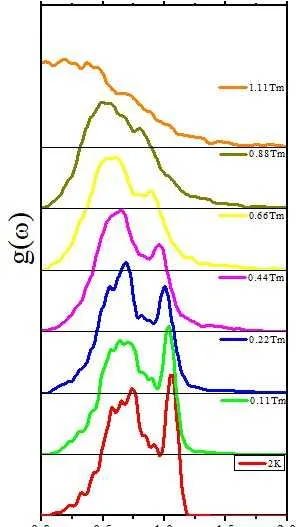
我們可以看到:(1)隨著溫度的升高,更多的聲子模向低頻偏移,這就是通常的大多數材料在高溫下的聲子軟化,在溫度升高的情況下,原子間距一般會增大,導致力常數較小,使得頻率減小,(這是與熱膨脹相對應的,當然有的材料在升溫下會熱縮);(2)隨著溫度升高,在高頻,聲子態密度有更長的拖尾效應,這是由於高溫下的聲子聲子相互作用(PPI)造成的,多個低頻聲子耦合為一個高頻聲子。
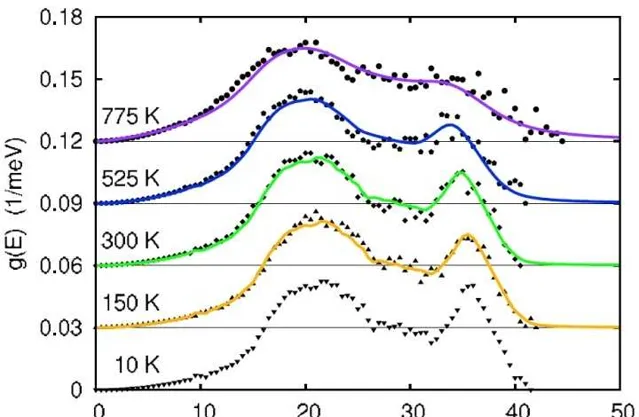
這個結果和上面計算的結果大體趨勢是差不多的。
二次量子化形式下的聲子頻率
系統的哈密頓量可以寫為
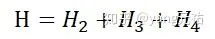

其中p,p,p分別為哈密頓量的二階項、三階項和四階項, \Phi 為力常數。三階項和四階項可進一步寫為(引入產生湮滅算符):
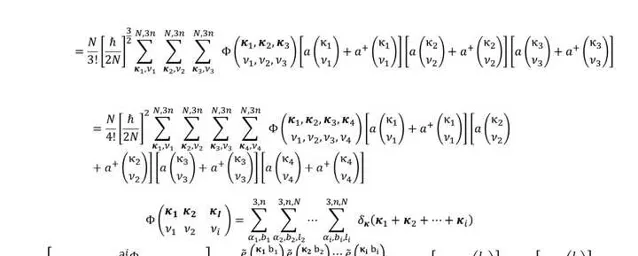
忽略中間的一些細節,得到聲子頻移

以上是一種計算非諧效應的方法。
裏面雖然沒有關聯到溫度,但實際上哈密頓量的三階項p和四階項p是和溫度有關的。 \Phi_{\alpha_1,\alpha_2,\alpha_3} 和\Phi_{\alpha_1,\alpha_2,\alpha_3,\alpha_4} 就是三聲子過程和四聲子過程。
一、簡諧近似下的聲子頻率
在教科書中,單原子鏈格波色散關系表示為:
\omega=2\sqrt{ \frac{\beta}{m} }|sin\frac{1}{2}aq|
連續介質彈性波 \omega=v_{s}q
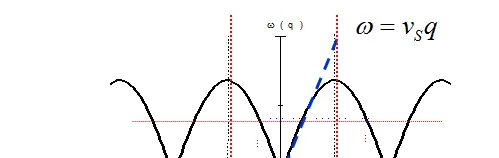
我們看到,聲子頻率只與 力常數\beta
有關。在簡諧近似處理下
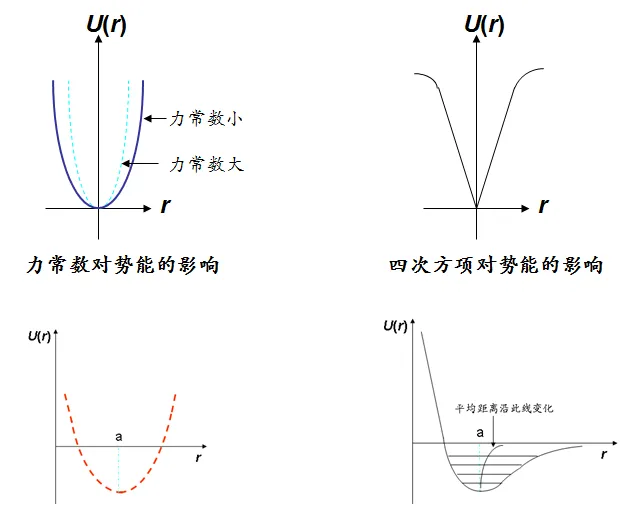
2、相互作用勢能的非簡諧項

非簡諧項,代表原子之間排斥作用的非對稱性
非簡諧項\frac{1}{6}g_{0}\delta^3 ,代表原子之間排斥作用的非對稱性,
δ>0時,\frac{1}{6}g_{0}\delta^3 小於0,勢能減小
δ<0時,\frac{1}{6}g_{0}\delta^3 大於0,勢能增大
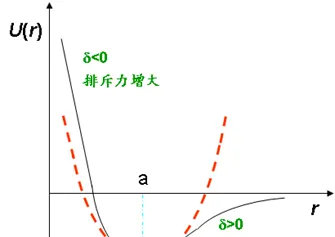
•考慮這一非簡諧項後,勢能曲線不對稱:δ>0一邊比較平緩,δ<0一邊則比較陡峭。因此非簡諧振動,使原子間產生一定的相互斥力,從而引起熱膨脹。所以熱膨脹是一種晶格振動的非簡諧效應。
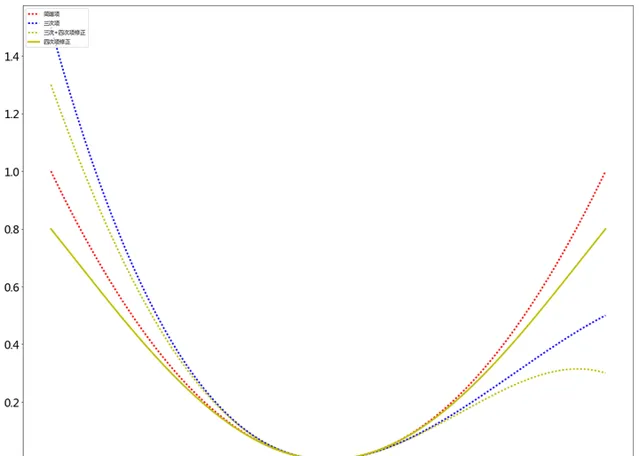
非簡諧項\frac{1}{24}h_{0}\delta^4 , 代表在大振幅下振動的軟化
考慮二階項和四階項,有
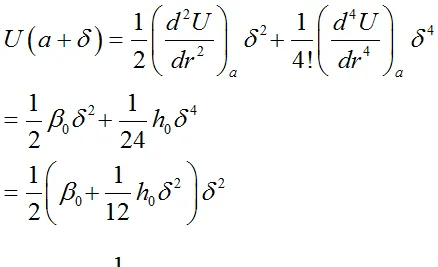
回復力常數減小,振動軟化。
U(a+\delta)=\frac{1}{2}\beta_{0}\delta^2+\frac{1}{6}g_{0}\delta^3+\frac{1}{24}h_{0}\delta^4
3.非簡諧近似下的解
(這個並不容易,因為現在的微分方程式已經不是簡單的二階常微分方程式)
考慮諧振子方程式中的非簡諧項,雙原子運動方程式
\mu \ddot{ \delta} =f(\delta) =-\frac{\partial U}{\partial \delta}=-\beta _0\delta-\frac{1}{2}g_0\delta^2 \\
μ是兩原子的約化質素
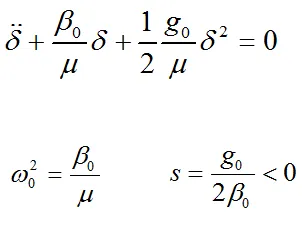
運動方程式解的形式\delta=v_{0}+A(cos(\omega t)+\eta cos(2\omega t))
這裏只考慮了Fourier展開式中的頭三項,所以只有2w項,如果考慮d3項,則會有3w的項。p將方程式的解代入運動方程式,並假定sA<<1,有
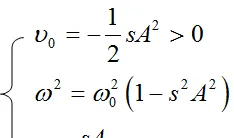
利用方程式的解,並考慮<coswt>=0, <cos2wt>=0

因為g0<0,所以a(T)>a
當系統與熱源處於熱平衡狀態時,雙原子的平均振動能
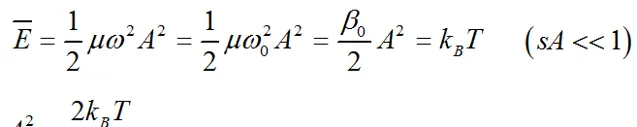
振幅的平方與溫度成正比
可以得到
a(T)=a_{0}-\frac{1}{2}\frac{g_{0}}{\beta_{0}^2}k_{B}T
\color {red} {\omega^2(T)=\omega_{0}^2(1-\frac{1}{2}\frac{g_{0}^2}{\beta_{0}^2}k_{B}T)}
隨著溫度的升高,原子間距離增大,作用力下降,振動頻率減小。上式就給出了頻率與溫度的關系,看起來簡單,但還需要求解 g , \beta ,此外,這個式子依然沒有考慮聲子耦合(PPI)。











