高斯在 數論(Number Theory) 中有著極其偉大的地位,那我們來聊一聊高斯在 虛數 i (Imaginary Number) 裏的了不起的貢獻。
正好最近閱讀了一些有關虛數 i 的問題,得到了許多知乎大佬的啟發. 發現自己之前回答的對於虛數的理解,有失偏頗,故此分享些自己對虛數在數論中的拙見.
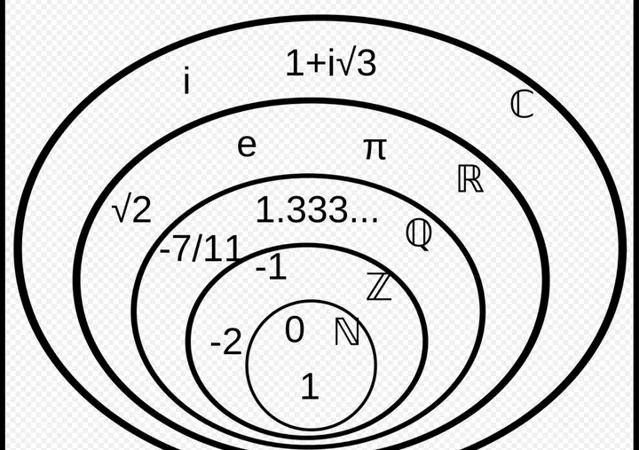
自從我回答了如何更形象地理解虛數 i 後,有小朋友會自然地發問:「為什麽會創造虛數i=\sqrt{-1} 呢?是我們現有的數不夠用了嘛?」很聰明喔!確實是不夠用了. 復數(complex number) z=a+bi 的引入是為了解決更多的方程式式. 事實上,我們曾為了解決方程式 3x-7=0 ,引入了 分數 的概念,故有 x=\frac{7}{3} . 我們需要引入 負數 才能夠解決 x+9=0 . 對於方程式 x^{2}-2=0 ,我們需要引入 無理數 的概念,故解得 \pm\sqrt{2} . 但是我們還是無法解決方程式 x^{2}+1=0 ,因為這個方程式在實數中沒有解. 所以我們自然會去 發明 * 新的數,從而去給出一個解.
* (盡管目前仍有不少數學家在爭論虛數 i 是發明還是發現,正如大家經常議論「 數學是被發現的還是被創造的 」,這些問題是引人入勝的哲學難題(就像大多數優秀的哲學問題一樣),它不太可能有一個明確的答案.)
那為什麽我們只需要引入一個虛數 i 呢?難道不再需要其他的虛數嗎?現在我們已經有 i=\sqrt{-1} 的概念了,可以去解決更復雜的方程式了,例如 (3+2i)x^{3}-(\sqrt{3}-5i)x^{2}-(\sqrt[7]{5}+\sqrt[3]{14}i)x+17-8i=0 .
如果這個方程式在我們的認知範圍內沒有解,我們則需要繼續創造更多的數碼. 令人意外的是,這個方程式的解還是復數的形式,
x_{1}=1.27609+0.72035i, x_{2}=0.03296-2.11802i, x_{3}=-1.67858-0.02264i .
事實上,我們有足夠多的復數去表示任意一個方程式的解,這便是
定理Ⅰ. 代數基本定理(The Fundamental Theorem of Algebra) 如果 a_{0},a_{1},a_{2},…,a_{d} 都是復數,並且 a_{0}\ne0,d\geq1 , 則 a_{0}x^{d}+a_{1}x^{d-1}+a_{2}x^{d-2}+…+a_{d-1}x+a_{d}=0 ,有一個解在復數體.
除此之外,我們再來看看復數的四則運算.復數相加減時,實部與虛部份別相加減,跟向量的加減法相同. 復數的乘法也同樣簡單,我們有 (a+bi)(c+di)=ac+adi+bci+bdi^{2}=(ac-bd)+(ad+bc)i .
對於復數的除法,我們用有理化它的分母,得到 \frac{a+bi}{c+di}=\frac{a+bi}{c+di}\cdot\frac{c-di}{c-di}=\frac{(ac+bd)+(-ad+bc)i}{c^{2}+d^{2}} .由此可見,它是封閉的,還是在復數體內.
在 數論(Number Theory) 中我們把形如 a+bi 且 a,b 均為整數的復數成為 高斯整數(Gaussian integers) . 高斯整數與之前我們在一年級學的整數有很多相同之處,而之前我們所認為的數軸上的整數是 b=0 時的高斯整數. 如果 a 和 b 是高斯整數,那麽它倆之和 a+b ,它倆之差 a-b ,它倆之積 ab 都是高斯整數. 但是,兩個高斯整數相除,不一定得到一個高斯整數. 例如 \frac{3+2i}{1-6i}=\frac{-9+20i}{37} 就不是一個高斯整數,但 \frac{16-11i}{3+2i}=2-5i 就是高斯整數.
現在我們來觀察復數的 因子分解(factorization) ,例如 1238-1484i=(2+3i)^{3}\cdot(-1+4i)\cdot(3+i)^{2} . 對於一般的整數 600=2^{3}\cdot3\cdot5^{2} ,我們可以更近一步化簡成高斯整數 600=-i\cdot(1+i)^{6}\cdot3\cdot(2+i)^{2}\cdot(2-i)^{2} .
我們知道任何一個一般的整數都可以被分解成若幹個質數因子,例如 7=1\cdot7 ,但我們也可以分解為 7=(-1)\cdot(-1)\cdot7 ,甚至還可以分解為 7=(-1)\cdot(-1)\cdot(-1)\cdot(-1)\cdot1\cdot1\cdot1\cdot1\cdot7 , 然後我們會意識到,如果不斷地添加1和-1,將會得到無窮多種分解方式. 那是什麽使得1和-1如此得與眾不同呢? 因為只有它們倆有 整數乘法逆元(integer multiplicative inverse) , 1\cdot1=1,(-1)\cdot(-1)=1 . 我們會發現如果整數 a 不是1或者-1,也就沒有另一個整數 b 可以滿足等式 ab=1 ,那 a 就不會有整數乘法逆元. 所以我們把1和-1叫做 單位元(units) . 那高斯整數中有 元素(element) 哪些是單位元呢?最先想起的是 i 本身,因為 i\cdot(-i)=1 , 這個等式同樣說明了 -i 也是一個單位元. 所以我們會繼續思考,除了 1,-1,i,-i 之外,是否還存在其他的單位元?
為了回答這個問題,我們先假設在高斯整數中存在另外的單位元 a+bi . 因為它是一個單位元,所有它一定有一個整數乘法逆元,使其乘積為1,故有 (a+bi)(c+di)=1 , 展開等式的左邊,得到 ac-bd=1,ad+bc=0 , 因此我們想找到滿足這兩個等式的解 (a,b,c,d) .
1^{0} 如果 a=0 , 則有 -bd=1 , 所以 b=\pm1,a+bi=\pm i ;
2^{0} 如果 b=0 , 則有 ac=1 , 所以 a=\pm1,a+bi=\pm1 ;
3^{0} 前兩種情況正好對應著我們已知的四個單位元,對於剩下兩種情況,我們假定 a\ne0 , b\ne0 , 則有c=\frac{1+bd}{a}\Rightarrow ad+b(\frac{1+bd}{a})=0\Rightarrow\frac{a^{2}d+b+b^{2}d}{a}=0 , 因為a\ne0 , 因此必須滿足等式 (a^{2}+b^{2})d=-b , 由此可知,a^{2}+b^{2} 需要整除 b ,但是 a^{2}+b^{2} 一定比 b 大,故該情況無解.
綜上所述,我們便可以得到
定理Ⅱ. 高斯單位元定理(Gaussian Unit Theorem) : 高斯整數中只有四個單位元,分別是 1,-1,i,-i ,只有它們有高斯整數乘法逆元.
值得註意的是,高斯整數是復數體的一個 子群(subset) ,而且子群裏所有元素的和,差以及乘積仍然在該子群中. 當然數軸上一般的整數亦有該性質. 在數學中,我們將擁有這個性質的集合稱之為 環(ring) .
再回到高斯整數的因子分解,我們可能會覺得如果一個高斯整數 \alpha 是一個質數,若且唯若只有 \pm1 和它本身能整除它. 但這樣定義會造成一個問題,因為我們總是可以寫出 \alpha=i\cdot (-i)\cdot\alpha ,因為任意的一個 \alpha 可以被 i,-i,i\alpha,-i\alpha 整除. 所以我們需要完善下最初的定義,便 有若且唯若高斯整數 \alpha 只能被 1,-1,i,-1,\alpha,-\alpha,i\alpha 和 -i\alpha 整除時,稱 \alpha 為高斯質數(Gaussian prime). 換言之,只有單位元和 \alpha 乘單位元能整除 \alpha .

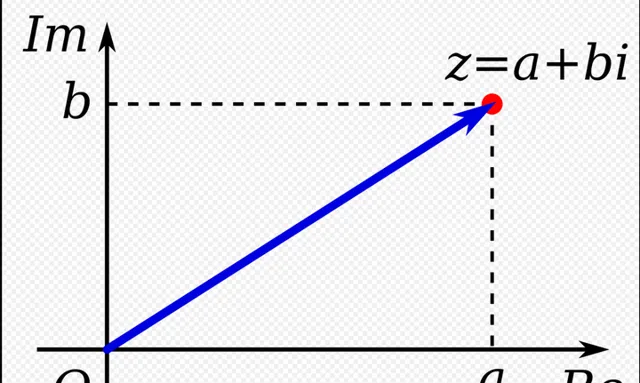
接下來我們就會探索,哪些數是高斯質數呢?舉個例子,你認為以下哪些數碼是高斯質數, 2,3,5,1+i,3+i,2+3i. 或許聰明的小朋友會根據剛剛的定義來判斷,更簡單的方法則是透過幾何來確定. 例如平面內一點 (a,b) , 其中 a,b 為整數. 那麽 (0,0) 到 (a,b) 的距離為 \sqrt{a^{2}+b^{2}} . 在數學中,我們用 範數(norm) 來刻畫長度和大小的數學概念,所以我們定義(a,b) 的 範數(norm) 寫作 N(a+bi)=a^{2}+b^{2} .
除此之外,範數在代數中有一條非常重要的性質:一個乘積的範數等於所有因子的範數之積. 因此我們就有
定理Ⅲ. (Norm Multiplication Property). 令 \alpha,\beta 為任意復數,則有 N(\alpha\beta)=N(\alpha)N(\beta) .
證明:令 \alpha=a+bi,\beta=c+di , 則有 \alpha\beta=(ac-bd)+(ad+bc)i , \alpha\beta 的範數為 (ac-bd)^{2}+(ad+bc)^{2} , \alpha 的範數和 \beta 的範數的乘積為 (a^{2}+b^{2})(c^{2}+d^{2}) . 因為 (ac-bd)^{2}+(ad+bc)^{2}=(a^{2}+b^{2})(c^{2}+d^{2}) ,故此定理成立.
在回到質因分解之前,我們不妨用範數去找單位元,或許能得到些新的啟發. 假設 \alpha=a+bi 是一個單位元,這說明存在 \beta=c+di 使得 \alpha\beta=1 . 同時在等式兩邊取範數,得到 N(\alpha)N(\beta)=N(\alpha\beta)=N(1)=1 , 則有 (a^{2}+b^{2})(c^{2}+d^{2})=1 . 但是 a,b,c,d 均為整數,所有我們一定有 a^{2}+b^{2}=1 ,此等式的整數解只有 (a,b)=(1,0),(-1,0),(0,1),(0,-1) , 這就再次證明了高斯單位元只有 1,-1,i,-i 這四個數. 同時我們亦得到一個重要的性質, 若且唯若高斯整數 \alpha 的範數 N(\alpha)=1 , \alpha 為高斯整數單位元.
接下來讓我們來嘗試分解幾個整數,例如2,令 (a+bi)(c+di)=2 , 等式兩邊同時取範數,得到 (a^{2}+b^{2})(c^{2}+d^{2})=4 ,
我們並不想讓等式的左邊出現單位元,顯然, (a^{2}+ b^{2})=2,(c^{2}+d^{2})=2 .
如果我們取 (a,b)=(1,1) , c+di=\frac{2}{1+i}=\frac{2(1-i)}{2}=1-i . 因此 2=(1+i)(1-i) ,有兩個其他的因子,所以2不是高斯質數.
用同樣的方法檢測3是否為高斯質數,最後得到 a^{2}+b^{2}=3,c^{2}+d^{2}=3 , 此時等式沒有正整數解,因此3是一個高斯質數. 另外,5可以被分解為 5=(2+i)(2-i) , 所以5並不是高斯質數.
把以上的過程一般化,如果有一高斯整數 \alpha ,令 \alpha=(a+bi)(c+di) , 取範數得到 (a^{2}+b^{2})(c^{2}+d^{2})=N(\alpha) , 我們並不希望得到括弧內的平方和等於1,因此我們要將範數 N(\alpha) 分解成 乘積AB 的形式,其中 A\ne1,B\ne1 . (以後我會寫一篇哪些數可以寫成兩個平方數之和的文章)
還是先做幾個簡單的例子,我們分解 \alpha=3+i ,其範數為 N(\alpha)=10=2\cdot5 , 因此我們需要解決 a^{2}+b^{2}=2,c^{2}+d^{2}=5 . 這兩個等式有多組解,比如 (a,b)=(1,1) , 可以得到 3+i=(1+i)(2-i) . 小朋友們可能想問,為什麽會有多組解呢?因為我們可以用不同的單位元去分解 3+i . 因此當 (a,b)=(-1,1) 時,我們也可以得到 3+i=(-1+i)(-1-2i) . 其實第二種分解本質上跟第一種一樣,因為我們有 -1+i=i(1+i),-1-2i=-i(2-i) .
再比如我們分解 \alpha=1+i , 其範數為 N(\alpha)=2 , 但 2 並不能被化簡為 2=AB(A,B>1) 的形式,因為 2 本身就是數軸上的質數. 這說明\alpha=1+i 是一個高斯質數. 不失一般性,如果 N(\alpha) 是一個質數,那麽 \alpha 就一定是一個高斯質數. 但這個性質也只說明了部份的高斯質數,比如 3,N(3)=9 ,這既是數軸上的質數亦是高斯質數. 接下來的定理便是此篇文章的壓軸戲,完整地揭示了滿足高斯質數的所有形式.
定理Ⅳ. 高斯質數定理(Gaussian Prime Theorem)
任何一個高斯質數可以被寫為以下三種形式之一:
(i) 1+i 是一個高斯質數.
(ii)如果 p 是數軸上的質數且 p\equiv3(mod 4) , 那麽 p 一定是一個高斯質數.
(iii)如果 p 是數軸上的質數且 p\equiv1(mod 4) , 將 p 寫成兩個平方數之和, p=u^{2}+v^{2} , 則有 u+vi 是一個高斯質數.
任何一個高斯質數可寫為定理(i)(ii)(iii)中高斯質數乘單位元( \pm1,\pm i )的形式.
說些題外話,大數學家們其實也是一群很可愛的人,喜歡給自己研究的數賦予各種各樣的名字(雖然有些名字聽起來離譜得很). 比如定理(i)中的高斯質數叫做 ramified ,定理(ii)叫做 inert ,定理(iii)叫做 split . 神奇之處就在於,它們還沒有自己的中文名喔,莫不是叫做「分歧,惰性,裂開」?!
這個定理的證明要運用一些初等數論的知識,比如同余,二次剩余和勒壤得二次互反律(筆者最愛的定理之一,會寫幾篇關於二次互反律的文章),還有平方數之和的質數的性質. 學習過數論的小朋友可以繼續閱讀以下的證明過程. 若只是感興趣的同學,可以先跳過證明部份,等待筆者隨後會分享的初等數論筆記,當你以後準備好的時候,再回來看看.
證明 :我們之前就觀察到如果 N(\alpha) 是質數,那麽 \alpha 就一定是高斯質數. 定理(i)中 1+i 的範數為 2 ,所以它是高斯質數. 同樣的,定理(iii)中 u+vi 的範數為 u^{2}+v^{2}=p , 所以這類數均為高斯質數.
接下來我們檢驗定理(ii),令 \alpha=p , 其中 p 是 p\equiv3(mod 4) 這一類別的質數. 如果 \alpha 可以被分解為 (a+bi)(c+di)=\alpha , 取範數得到 (a^{2}+b^{2})(c^{2}+d^{2})=N(\alpha)=p^{2} , 所以我們就需要解決等式 a^{2}+b^{2}=p 和 c^{2}+d^{2}=p . 但我們知道可以寫成兩個平方和的質數若且唯若 p\equiv1(mod 4) ,而這裏是 p\equiv3(mod 4) ,所以這兩個等式無正整陣列解,因此 p 不可被分解,故此為高斯質數.
現在我們已經證實了定理(i)(ii)(iii)中所描述的皆為高斯質數,接下來要做的就是證明每一個高斯質數都在這三種形式裏面. 為了證明這一點,我們便要拿出一個更強大的工具——新的引理!
引理Ⅴ. 高斯可除性引理(Gaussian Divisibility Lemma)
令 \alpha=a+bi 是一個高斯整數,則有
(a)如果 2 可以整除 N(\alpha) ,那麽 1+i 可以整除 \alpha ;
(b)令 \pi=p ,且 p 為定理Ⅳ(ii)中的質數,如果 p 可以作為質數整除 N(\alpha) ,那麽 \pi 可以作為高斯質數整除 \alpha ;
(c)令 \pi=u+vi 為一個高斯質數且滿足定理Ⅳ(iii),令 \bar{\pi}=u-vi ,( \bar{\pi} 通常表示為共軛復數conjugate complex number),如果 N(\pi)=p 可以作為質數整除 N(\alpha) , 那麽 \pi,\bar{\pi} 中有一個可以作為高斯質數整除 N(\pi) .
引理Ⅴ證明 :(a) 我們有2 整除 N(\alpha)=a^{2}+b^{2} , 所以 a,b 要麽是都為奇數,或者是都為偶數. 這說明 a+b 和 -a+b 都可以被 2 整除,因此 \frac{a+bi}{1+i}=\frac{(a+b)+(-a+b)i}{2} 是高斯整數,故 a+bi 可以被 1+i 整除.
(b)我們有 p\equiv3(mod 4) 並且 p 整除 a^{2}+b^{2} ,這說明 a^{2}+b^{2}\equiv0(modp)\Rightarrow a^{2}\equiv-b^{2}(modp) , 使用勒壤得符號得到 \left(\frac{a}{p} \right)^{2}=\left( \frac{a^{2}}{p} \right)=\left(\frac{-b^{2}}{p}\right)=\left( \frac{-1}{p} \right)\left( \frac{b}{p}\right)^2 . 因為 p\equiv3(mod 4) ,根據二次互反律 \left( \frac{-1}{p}\right)=-1 ,我們可以得到 \left( \frac{a}{p} \right)^2=-\left( \frac{b}{p} \right)^2 , 但是似乎我們最後得到的是 1=-1 ,是哪裏出了問題呢?因為勒壤得符號 \left( \frac{a}{p} \right) 只針對 a,p 兩數不能整除的情況. 從得到的矛盾來看,這意味著 a,b 必須同時滿足被 p 整除的條件,所以 a=pa^{'},b=pb^{'} . 因此 \alpha=a+bi=p(a^{'}+b^{'}i) 被 p=\pi 整除.
(c) 我們有 p 整除 N(\alpha) ,則 a^{2}+b^{2}=N(\alpha)=pK , 對於一些整數 K\geq1 . 然後我們需要證明 \frac{\alpha}{\pi}=\frac{(au+bv)+(-av+bu)i}{p} 或 \frac{\alpha}{\bar{\pi}}=\frac{(au-bv)+(av+bu)i}{p} 是一個高斯整數.
首先我們可以觀察到 (au+bv)(au-bv)=a^{2}u^{2}-b^{2}v^{2}=a^{2}u^{2}-b^{2}(p-u^{2}) =(a^{2}+b^{2})u^{2}-pb^{2}=pKu^{2}-pb^{2}
所以 p 可以整除 (au+bv) 或者 (au-bv) .
根據另一個與上述相似的計算,得到 (-av+bu)(av+bu)=pKu^{2}-pa^{2} ,
所以 p 可以整除 (-av+bu) 或 (av+bu) .
接下來就需要分情況討論,分別是:
① p 可以整除 au+bv,-av+bu ;
② p 可以整除 au+bv,av+bu ;
③ p 可以整除 au-bv,-av+bu ;
④ p 可以整除 au-bv, av+bu ;
情況①很容易證明,因為它直接意味著 \frac{\alpha}{\pi} 是高斯整數,所以 \pi 整除 \alpha .
同理可證④,所以 \bar{\pi} 整除 \alpha .
然後我們驗證②, 推匯出 p 可以整除 (au+bv)b-(av+bu)a=(b^{2}-a^{2})v . 因為 p 不整除 v 但 p 整除 a^{2}+b^{2} ,
所以我們發現 p 同時整除 2a^{2}=(a^{2}+b^{2})-(b^{2}-a^{2}),2b^{2}=(a^{2}+b^{2})+(b^{2}-a^{2}) .
並且 p\ne2 ,我們最終推匯出 p 同時整除 a,b ,且令 a=pa^{'},b=pb^{'} ,
則有 \alpha=a+bi=p(a^{'}+b^{'}i)=(u^{2}+v^{2})(a^{'}+b^{'}i)=\pi\bar{\pi}(a^{'}+b^{'}i) , 因此我們得到 \alpha 同時可被 \pi,\bar{\pi} 整除.
同理可證③,所以\alpha 同時可被 \pi,\bar{\pi} 整除.
重回定理Ⅳ的證明: 假設 \alpha=(a+bi) 是任意一個高斯質數,我們要做的就是證明 \alpha 一定是在定理Ⅳ的三種類別裏. 因為我們知道 \alpha 不是單位元,所以N(\alpha)\ne1 ,至少存在一個質數可以整除N(\alpha) .
首先假設 p=2 ,引理Ⅴ(a)告訴我們1+i 可以整除 \alpha ,但是 \alpha 應為質數,所以這說明 \alpha 是單位元乘 1+i 的形式,故為定理Ⅳ(i)中的高斯質數;
再假設 p\equiv3(mod 4) ,引理Ⅴ(b)告訴我們p 可以整除 \alpha ,所以\alpha 是單位元乘 p 的形式,故為定理Ⅳ(ii)中的高斯質數;
最後假設 p\equiv1(mod 4) ,因此 p 可以寫成兩個平方數之和, p=u^{2}+v^{2} . 根據引理Ⅴ(c), \alpha 會被 u+vi 或者 u-vi 整除. 因此 \alpha 為單位元與 u+vi 或者 u-vi 的乘積. 特別地, a^{2}+b^{2}=u^{2}+v^{2}=p , 故 \alpha 為定理Ⅳ(iii)中的高斯質數.
以上我們便完整地說明了每個高斯質數都符合這三種形式的其中之一,完成 高斯質數定理 的證明.











