博弈論中的機制設計可以用演化演算法自動實作嗎?
博弈論中的機制設計完全可以用演化演算法自動實作!實際上最著名的工作還是微軟劉鐵巖教授的博弈機器學習那篇論文。但是,遠在2003年,演化計算領域就已經出現了用演化演算法實作機制設計的論文。這裏我以2003年的一篇文章【Using genetic programming to optimise pricing rules for a double auction market】簡單介紹一下如何使用演化演算法實作電價交易市場中的定價策略制定。這篇文章是非常早期的演化機制設計論文,因此並沒有取得很顯著的效果,對演化機制設計感興趣的同學可以進一步閱讀Steve Phelps的博士論文以了解更多的相關研究。
問題描述
該論文主要將嘗試使用遺傳編程演算法設計電價交易策略。具體來說,電價交易市場存在多個買家和賣家,並有一個交易中介機構。買家和賣家都有自己的預期出價。中介機構根據買家和賣家的出價進行匹配,並敲定最終的價格。而機制設計的目的就是希望透過良好的機制實作整體市場的利益最大化。
評估函數
對於一個交易策略,其評估函數由多方面構成,例如市場效率,買家偏向和賣家偏向。
首先,整個市場效率可以使用下面公式進行定義。PBA代表買家的實際收益,PSA代表賣家的實際收益。PBE代表買家的理想收益,PSE代表賣家的理想收益。

買家能力MPB,定義為定價策略對買家的偏向。具體來說,即當前收益PBA和理想市場情況下的理想收益PBE之間的差值,除以PBE。這個值越小代表定價策略越有利於買家。
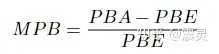
同樣的,也可以定義定價策略對賣家的偏向,MPS,這個值越小代表定價策略越有利於賣家。

此外,還可以根據當前市場情況下的理想收益與當前收益的差距定義SMPB和SMPS,具體定義方法可以參考論文。
為了保證所有評估函數最佳值為1,最差值為0。作者按照下面的方法定義了五個評估函數。

聚合上面的評估函數,可以得到下面兩個評估函數。
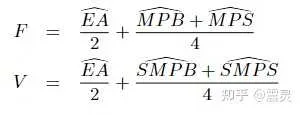
在經典的交易機制設計領域,目前常用的一個基準機制是取買家出價和賣家出價的加權和作為最終成交價格,即如下公式所示。在論文中,作者選擇 k=0.5 ,即取平均值作為最終價格。
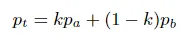
搜尋演算法
論文使用了遺傳編程演算法對定價策略進行搜尋,具體來說就是透過演化演算法嘗試使用數學運算子組合賣家出價 p_a 和買家出價 p_b ,形成最終的市場定價。對於每一個搜尋出的定價策略,都透過仿真環境進行交易模擬,並透過上面的評估函數進行評估。
實驗結果
最終實驗得到了如下所示的定價策略,單單從公式上來看,這裏遺傳編程演算法演化出了一個非常復雜的公式。
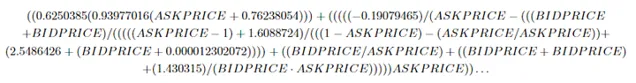
為了簡化理解,作者將該公式所對應的定價曲面在下圖中進行了繪制。可以發現,遺傳編程所發現的定價策略和經典的均值定價策略具有相似的曲面。這意味著模型透過演化演算法可以自動發現類似均值定價策略的策略。












