這個問題必須加一個前置條件,即自底向上 (bottom-up) 的建堆方式,也就是 Floyd 建堆演算法。因為方向相反、自頂向下 (top-down) 的建堆方式的時間復雜度為 O(n·logn).
因此問題應該是 Floyd 建堆演算法的時間復雜度為什麽是 O(n) ?
關鍵詞:等差-等比數列求和,錯位相減法,等比數列求和公式。
首先設定研究這個問題的前置條件:
假設目標堆是一個滿堆,即第 k 層節點數為 2ᵏ。輸入陣列規模為 n, 堆的高度為 h, 那麽 n 與 h 之間滿足 n=2ʰ⁺¹ - 1 ,可化為 h=log₂(n+1) - 1 。 (層數 k 和高度 h 均從 0 開始 ,即只有根節點的堆高度為0,空堆高度為 -1)。
建堆過程中每個節點需要一次下濾操作,交換的次數等於該節點到葉節點的深度。那麽每一層中所有節點的交換次數為節點個數乘以葉節點到該節點的深度(如第一層的交換次數為 2⁰ · h,第二層的交換次數為 2¹ · (h-1),如此類推)。從堆頂到最後一層的交換次數 Sn 進行求和:
Sn = 2⁰ · h + 2¹ · (h - 1) + 2² · (h - 2) + ...... + 2ʰ⁻² · 2 + 2ʰ⁻¹ · 1 + 2ʰ · 0
把首尾兩個元素簡化,記為①式:
①: Sn = h + 2¹ · (h - 1) + 2² · (h - 2) + ...... + 2ʰ⁻² · 2 + 2ʰ⁻¹
對①等於號左右兩邊乘以2,記為②式:
②: 2Sn = 2¹ · h + 2² · (h - 1) + 2³ · (h - 2) + ...... + 2ʰ⁻¹ · 2 + 2ʰ
那麽用②式減去①式,其中②式的運算元右移一位使指數相同的部份對齊(即錯位相減法):
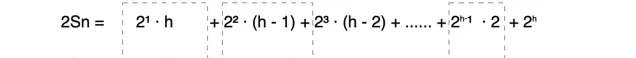
化簡可得③式:
③ = Sn = -h + 2¹ + 2² + 2³ + ...... + 2ʰ⁻¹ + 2ʰ
對指數部份使用等比數列求和公式:Sn=\frac{a_{1}\times\left( 1-q^{n} \right)}{1-q}
在這個等比數列中,a1=2, q=2,則③式為:
Sn=-h+\left( \frac{2\times\left( 1-2^{h} \right)}{\left( 1 - 2 \right)} \right)
化簡為④式:
④ = Sn = 2ʰ⁺¹ - (h + 2)
在前置條件中已得到堆的節點數 n 與高度 h 滿足條件 n=2ʰ⁺¹ - 1(即 2ʰ⁺¹=n+1) 和 h=log₂(n+1) - 1,分別代入④式中的 2ʰ⁺¹ 和 h,因此:
Sn=\left( n + 1 \right) - \left( log_{2}\left( n+1 \right) - 1 + 2 \right)
化簡後為:
Sn = n - log₂(n + 1)
因此最終可得漸進復雜度為 O(n).
(補充一下個人看法)
由於對數的部份 log₂(n + 1) 是一個正數,所以 n - log₂(n + 1) < n ,因此最終結果不僅從漸進角度而言為 O(n), 從常系數的角度來說,是比 O(1n) 更優。即 O(an), 0 < a < 1;











