高贊說的沒錯
本質上就是圓的外切正六邊形的面積
S_{1}=6\cdot\frac{1}{2}\cdot\frac{2\sqrt{3}}{3}r^{2}=2\sqrt{3}r^{2}
和內接正八邊形的面積
S_{2}=8\cdot\frac{1}{2}r^{2}\sin\frac{\pi}{4}=2\sqrt{2}r^{2}
的平均值
實際上,在數學史中,利用圓的內接或外切正多邊形的周長或面積,去逼近圓的周長或面積,是早期數學家們的常規思路,舉兩個例子:
考慮一個數列問題:
數列 \left\{ a_{n} \right\} 、 \left\{ b_{n} \right\} ,滿足 a_{1}=2\sqrt{3} , b_{1}=3 , a_{n+1}=\frac{2a_{n}b_{n}}{a_{n}+b_{n}} , b_{n+1}=\sqrt{a_{n+1}b_{n}} .
求數列 \left\{ a_{n} \right\} 、 \left\{ b_{n} \right\} 的通項公式.
這實際上是2200多年前,古希臘數學家阿基米德使用的割圓術
他本質上使用圓的外切正 3\cdot2^{n} 邊形的周長,以及內接正 3\cdot2^{n} 邊形的周長,去逼近圓周長
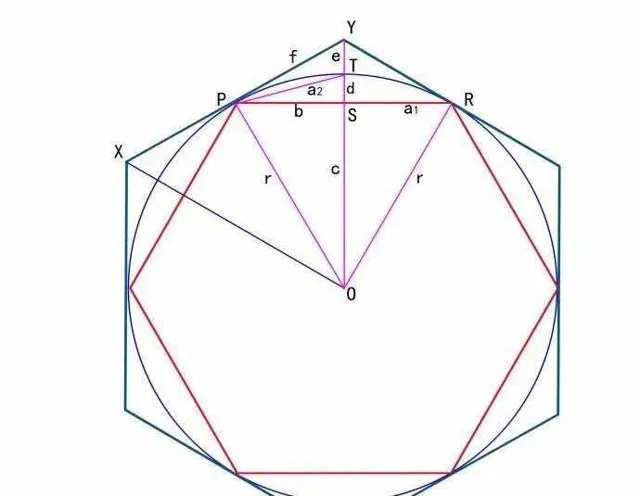
而 a_{n} 和 b_{n} 的幾何意義,分別是圓的外切正 3\cdot2^{n} 邊形的周長與圓直徑的比值,以及內接正 3\cdot2^{n} 邊形的周長與圓直徑的比值
詳見:
而劉徽則使用了另一種方法:
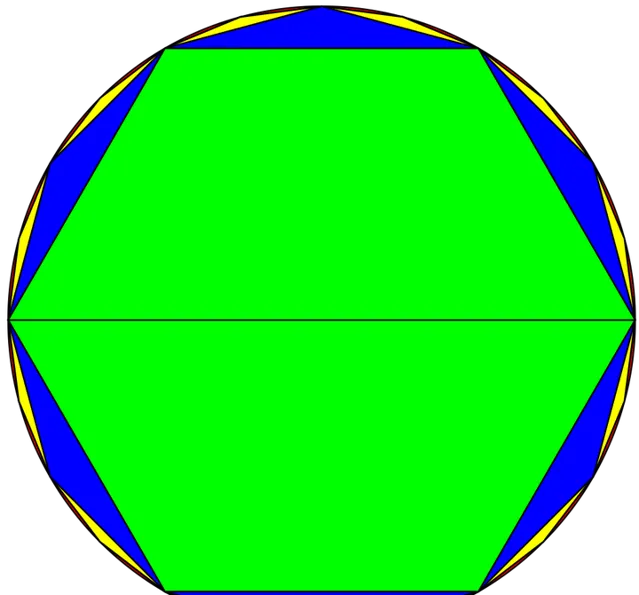
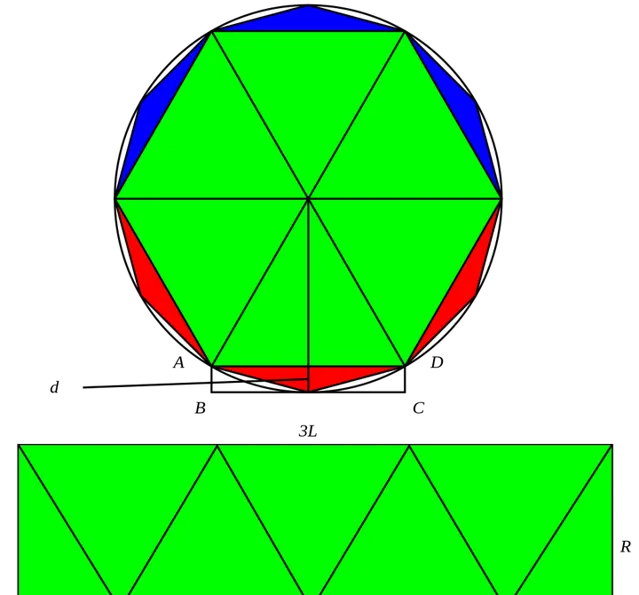
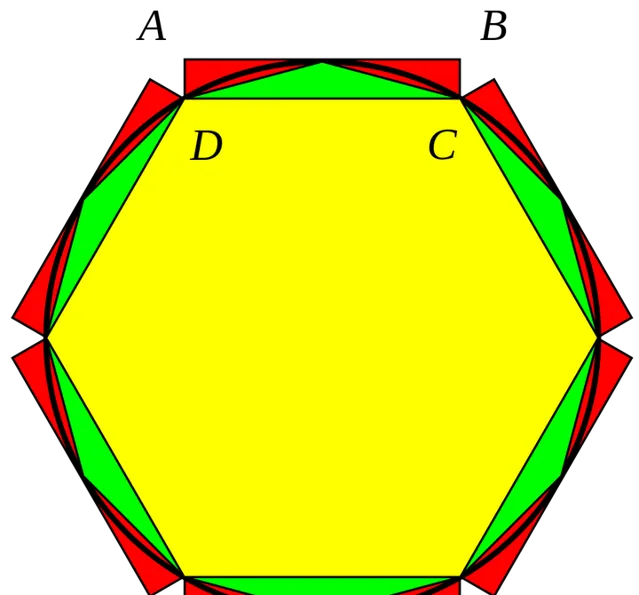
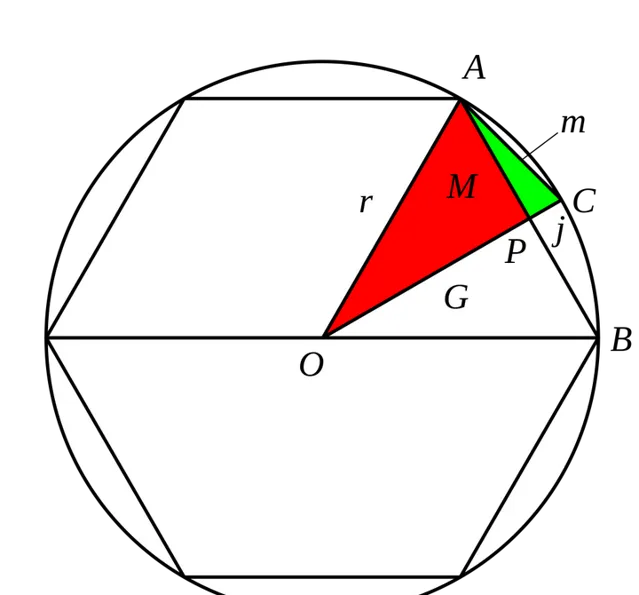
定義 A_{n} 為圓的內接正 3\cdot2^{n} 邊形的面積, l_{n} 為圓的內接正 3\cdot2^{n} 邊形的邊長
那麽由幾何關系,顯然有:
A_{n+1}=3\cdot 2^{n-1}\cdot r\cdot l_{n}
令圓面積為 A ,(根據幾何關系)則有如下 劉徽不等式 :
A_{n+1}<A<2A_{n+1}-A_{n}
劉徽使用圓的內接正 3\cdot2^{n}
邊形的面積去逼近圓面積
詳見:











