數據分析學習筆記——統計學基礎

1 為什麽要了解統計學

對於普羅大眾來說，統計學應該會成為每人必備的常識，才能避免被越來越精致的數碼陷阱欺騙。起碼當你看到各種百分比和收益率，能多出一份警覺，多思考些他們的來源和計算途徑。

對於互聯網工作者來說，統計知識投射在互聯網上，就是數據相關的方法論。舉例來講，現在盛行的 A/B Test 本質上就是控制變量法實驗中的一種。不同的是，互聯網獲取數據更簡單，進行對比實驗更方便。這將是一個統計學/數據分析的大事件。想象一下 Facebook 內部幾千個 A/B Gate，簡直稱得上一場史無前例的大規模人口社會實驗。

這也是為什麽近些年來 Growth Hacker ，Data Scientist 越來越火的原因。數據量的極易獲取，計算儲存成本的降低和分析效率的提升，使得統計分析的成本更低，規模更大，從而輸出價值更高。

統計和分析的差別

個人理解上，統計分析應該是整個數據流程的不同部份。統計在於工具或手段，分析更偏重理念。比如回歸分析為什麽叫分析不叫統計，就是因為其中已經包含了部份歸因的思想。再舉個栗子，決定對一批數據取平均數還是中位數，這是統計，該怎麽利用，是分析。

如【赤裸裸的統計學】中指出來的一樣，統計分析是：

1. 總結大量的數據
2. 做出正確的決定
3. 回答重要的社會問題
4. 認識並改善我們日常的行為模型

2 統計學入門基礎

統計學分為描述性統計學和推斷性統計學。

描述性統計

定義：使用特定的數碼或圖表來體現數據的集中程度和離散程度。

集中趨勢

集中趨勢集中趨勢是指一組數據所趨向的中心數值，用到的指標有：算數均數、幾何均數、中位數。

算數均數：即為均數，用以反映一組呈對稱分布的變量值在數量上的平均水平。

幾何均數：常用以反映一組經對數轉換後呈對稱分布的變量值在數量上的平均水平。

中位數：適用於偏態分布資料和一端或兩端無確切的數值的資料，是第50百分位數。

百分位數：為一界值，用以確定醫學參考值範圍。

離散趨勢

離散趨勢是反映數據的變異程度，常用指標有極差、四分位間距、變異數與標準差、變異系數。

極差：為一組數據的最大值和最小值之差，但極差不能反映所有數據的變異大小，且極易受樣本含量的影響。常用以描述偏態分布。

四分位數間距：它是由第3四分位數與第1四分位數相減得到，常和中位數一起描述偏態分布資料的分布。

變異數與標準差：反映一組數據的平均離散水平，消除了樣本含量的影響，常和均數一起用來描述一組數據中的離散和集中趨勢。

標準分：也叫z分數，是一種具有相等單位的量數。它是將原始分數與團體的平均數之差除以標準差所得的商數，是以標準差為單位度量原始分數離開其平均數的分數之上多少個標準差，或是在平均數之下多少個標準差。它是一個抽象值，不受原始測量單位的影響，並可接受進一步的統計處理。用公式表示為：z=(x-μ)/σ;其中z為標準分數；x為某一具體分數，μ為平均數，σ為標準差。標準分表示【某個數值】距離平均值多少個標準差。在質素管理中，我們常常聽到6西格瑪管理就是標準分的典型套用。這個標準差，通常用每百萬次采樣數的缺陷率來衡量。

變異系數：也稱作異常值，多用於觀察指標單位不同時，可消除因單位不同而不能進行比較的困難。

例如箱線圖就可以很好反映其中部份重點統計值：

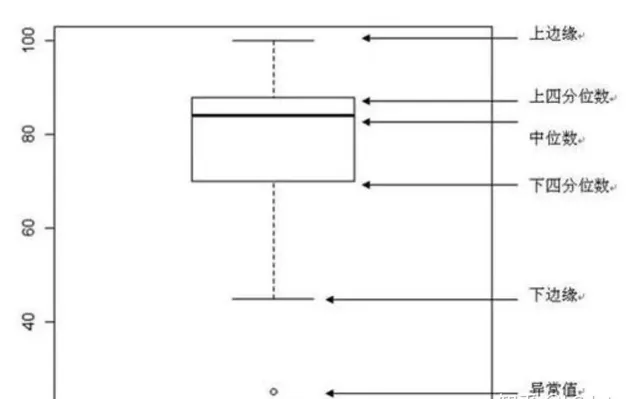抽樣方法和中央極限定理

抽樣方法：

我們在做產品檢驗的時候，不可能把所有的產品都開啟檢驗一遍看是否合格，我們只能從全部的產品中抽取部份樣本進行檢驗，依據樣本的質素估算整體的產品質素，這個就是抽樣，抽樣的定義是為了檢驗整體從整體中抽離部份樣本進行檢測，以樣本的檢測結果進行整體質素的估算的方法。

抽樣有多種方法，針對不同的目的和場景，需要運用不同的方法進行檢測，常見的抽樣方法有：

1）概率抽樣

簡單隨機抽樣；

分層抽樣；

集體取樣（先將總體中若幹個單位合並為組，這樣的組稱為群，再直接對群進行抽樣）；

系統抽樣（將總體中所有單位按一定順序排列，在規定的範圍內隨機抽取一個單位作為初始單位，然後再按事先指定好的規則確定其他樣本單位）；

階段抽樣（先抽群，然後在群內進行二階段抽樣）。

2）非概率抽樣

方便抽樣（依據方便原則自行確定）；

判斷抽樣（依據專業知識進行判斷）；

自願樣本（調查者自願參加）；

滾雪球樣本（類似樹結構）；

配額樣本（類似分層抽樣）；

3）兩者抽樣方法之間的比較：

非概率抽樣適合探索性的研究，為更深入的數據分析做準備，特點是操作簡便、時效快、成本低；而且對於抽樣中的統計專業技術要求不是很高；

概率抽樣的技術含量更高，調查成本更高，統計學專業知識要求更高，適合調查目的為研究物件總體，得到總體參數的置信區間。

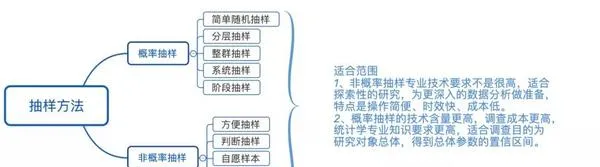
4）中央極限定理：

若給定樣本量的所有樣本來自任意整體，則樣本均值的抽樣分布近似服從正態分布，且樣本量越大，近似性越強。

以30為界限，當樣本量大於30的時候符合中央極限定理，樣本服從正態分布；當樣本量小於30的時候，總體近似正態分布時，此時樣本服從t分布。樣本的分布形態決定了我們在假設檢驗中采用什麽方法去檢驗它。

描述性分析思維總結

1. 集中趨勢的描述性統計

均值：描述一組數據的平均水平，是集中趨勢中波動最小、最可靠的指標，但是均值容易受到極端值（極小值或極大值）的影響。

中位數:最適合的表征集中趨勢的指標。

眾數：常用於描述定性數據的集中趨勢，不受極端值的影響。

2. 離散程度的描述性統計

最大值和最小值：是一組數據中的最大觀測值和最小觀測值。

極差：一般情況下，極差越大，離散程度越大，其值容易受到極端值的影響。

變異數和標準差：是描述一組數據離散程度的最常用、最適用的指標，值越大，表明數據的離散程度越大。

3. 分布形態的描述性統計

偏度：當偏度=0時，分布是對稱的；當偏度>0時，分布呈正偏態；當偏度<0時，分布呈負偏態。

峰度：當峰度=0時，分布和正態分布基本一直；當峰度>0時，分布形態高狹；當峰度<0時，分布形態低闊。

4. 頻率統計分析

頻數分布分析（又稱頻率分析）主要透過頻數分布表、條形圖和直方圖、百分位值等來描述數據的分布特征。

在做頻數分布分析時，通常按照定性數據（即分類的類別），統計各個分類的頻數，計算各個分類所占的百分比，進而得到頻率分布表，最後根據頻率分布表來繪制頻率分布圖。

5. 按照時間遞增的趨勢統計

特殊情況下，當X軸是日期數據，Y軸是統計量（比如均值、總數量）時，可以繪制出統計量按照時間遞增的趨勢圖，從圖中可以看到統計量按照時間增加的趨勢（無變化、遞增或遞減）和周期性。

例如，下圖的X軸是日期，Y軸的統計量是總數量，兩條折線分別是新增企業數和新增使用者數據

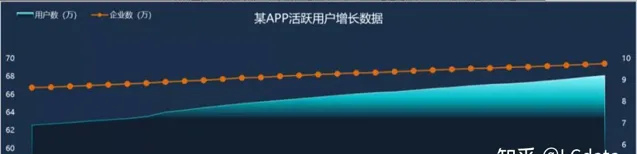描述性分析思維運用基本思路

首先，要描述目前的數據表現的現狀是什麽 ，根據分析目的，提取指標數據的具體數值：如數量、平均數、極差、標準差、變異數、極值。

其次，描述分布規律 ：如均勻分布、正態分布、集中趨勢、長尾分布。

然後 ，根據以往的數據的或者是之前制定的標準， 制定參考標準 。

最後，綜合現狀和標準，輸出有價值的結論，並進行視覺化 ：如柱狀圖、條形圖、散點圖、餅狀圖。

只有業務概況+數據指標+標準（視覺化）才能得出一個「是什麽」的結論。

業務概況+數據指標+標準（視覺化）=結論的分析流程，非常簡單，不過標準如何去制定？那又是需要我們深思的問題了。

例如，一個門店購買商品的數量的平均值是多少？四分位數是多少？標準差是多少？標準分是多少？兩個數據的變異系數是多少？

一個門店銷量每日增長趨勢怎麽樣？客單價的分布如何？成什麽分布？門店總銷量是多少？哪個商品賣得最好？細分的品類中賣的最好的是什麽？

例如麪包中，是有鮮奶油麪包的好，還是無脂麪包=賣的好？什麽時間使用者購買最集中，一天中哪個時間段購買最集中，賣得最好？

推斷性統計

定義：根據樣本數據推斷總體的數據特征。

基本步驟

產品質檢的時候用的幾乎都是抽樣方法的推斷性統計，推斷性的過程就是一種假設檢驗，在做推斷性統計的時候我們需要明確幾點：

問題是什麽？

需要明確的證據是什麽？

判斷標準是什麽？

明確後可以對應我們假設檢驗的幾個步驟了：

提出原假設（H0）和備選假設（p），確定顯著性水平（原假設為正確時，人們把它拒絕了的概率）；

選擇檢驗方法，確定檢驗統計量；

確定P值，作出統計推理；

假設對於某一個器件，國家標準要求：平均值要低於20。

某公司制造出10個器件，相關數值如下：15.6、16.2、22.5、20.5、16.4、19.4、16.6、17.9、12.7、13.9。

運用假設檢驗判斷該公司器件是否符合國家標準：

1）設假設：

原假設：器件平均值>=20；

備擇假設：器件平均值<20；

2）總體為正態分布，變異數未知，樣本為小樣本，因此采用T檢驗。

3）計算檢驗統計量：樣本平均值17.17，樣本標準差2.98，檢驗統計量為 （17.17-20）/（2.98/√10）=-3.0031

4）當置信度選擇97.5%，自由度為9，此時為單尾檢驗，臨界值為2.262。

5）由於-3.0031<-2.262，拒絕原假設，因此接受備擇假設，該器件滿足國家標準。

假設檢驗類別

單樣本檢驗：檢驗單個樣本的平均值是否等於目標值；

相關配對檢驗：檢驗相關或配對觀測之差的平均值是否等於目標值；

獨立雙樣本檢驗：檢驗兩個獨立樣本的平均值之差是否等於目標值；

統計檢驗方法

Z檢驗：一般用於大樣本（即樣本容量大於30）平均值差異性檢驗的方法。它是用標準正態分布的理論來推斷差異發生的概率，從而比較兩個平均數>平均數的差異是否顯著。

T檢驗：用於樣本含量較小（例如n<30），總體標準差σ未知的正態分布樣本。

F檢驗：F檢驗又叫變異數齊性檢驗。在兩樣本t檢驗中要用到F檢驗。檢驗兩個樣本的變異數是否有顯著性差異 這是選擇何種T檢驗（等變異數雙樣本檢驗，異變異數雙樣本檢驗）的前提條件。

（T檢驗用來檢測數據的準確度，檢測系統誤差 ；F檢驗用來檢測數據的精密度，檢測偶然誤差。）

隨機誤差：也稱為偶然誤差和不定誤差，是由於在測定過程中一系列有關因素微小的隨機波動而形成的具有相互抵償性的誤差。

系統誤差：指一種非隨機性誤差。如違反隨機原則的偏向性誤差，在抽樣中由登記記錄造成的誤差等。它使總體特征值在樣本中變得過高或過低。

卡方檢驗：主要用於檢驗兩個或兩個以上樣本率或構成比之間差別的顯著性，也可檢驗兩類事物之間是否存在一定的關系。

雙尾檢測和單尾檢測

這個和我們提出的原假設相關，例如我們檢測的原假設：器件平均值>=20。

我們需要拒絕的假設就是器件平均值<20，此時就是單尾檢驗；

如果我們的原假設是器件平均值>20，則我們需要拒絕的假設就是器件平均值<20和器件平均值=20，此時就是雙尾檢測。

置信區間和置信水平

在統計學中，幾乎都是依據樣本來推斷總體的情況的，但在推斷的過程中，我們會遇到各種各樣的阻礙和幹擾；所以我們推斷出的結果不是一個切確的數碼，而是在某個合理的區間內，這個範圍就是置信區間。

但整體中所有的數據都在這個範圍也不現實，我們只需要絕大多數出現在置信區間就可以了，這裏的絕大多數就是置信水平的概念，通常情況我們的置信水平是95%。

置信區間[a，b]的計算方法為：（z分數：由置信水平決定，查表得。）

a = 樣本均值 – z 標準誤差，b = 樣本均值 + z 標準誤差

3 分析中的統計學陷阱

陷阱 一：統計指標各有利弊

透過選擇合適的統計指標，來精準表達數據集的內容。同時也需要防止有人利用這些指標的優缺點來誤導輿論，影響你的決策。

1. 平均數，中位數，四分位數 ： 平均數對極值敏感而中位數不會。如果看中位數和四分位數，可能情況就會大不相同。
2. 絕對值，比率值 ：註冊數是絕對值，註冊率是比率值。比率值出現異常時，需要首先關註分子和分母的情況。比如說，某天發現網站 UV 周同比上漲了 500%，有可能是上周基數太低導致的。如果一上來就從維度進行細分，很容易跑偏。
3. 百分比，百分差，百分率 ：百分比是個常見的數據表達形式，其中貓膩也比較多。此類數碼往往需要註意分母和分子的差別。以下是兩個常見例子：1，一件貨品先降價15%再漲15%價格是否一樣？2，對於百分差和百分率，稅率從3%漲到5%，可以說上漲了2個百分點，也可以說上漲了67%，給人感覺效果大不一樣。
4. 指數型數據 ：即透過各項數據計算得出來的指數，優點在於將所有資訊濃縮成一個數碼，簡單易懂，但容易忽略其中成分數據的影響。美團外賣當初有個很復雜的考核城市使用者體驗的指標，就是個很好的例子。透過多項數據的整合，我們很好地把使用者體驗這種比較虛的東西落到了實處。不過需要註意的是，對它的過分依賴容易帶來誤導性的結論。

陷阱 二：統計背景不夠明確

1. 首先要了解： 精確和準確是有本質差別的 。如在你內急的時候我告訴你公廁在你右邊直走134.12m處，這很精確。不過實際上，廁所在左邊。準確的要義是要能讓指標貼近所描述事物。
   
2. 這需要 在衡量事物的指標上達成統一 。如在之前 20011 年時有爭論：美國制造業是否正在衰退？從總體產出上看，從 2000 年來看一直在增長，而制造業的就業數卻在下降。因此需要統一指標來表述制造業的繁榮情況。就像電商一樣，需要明確自己當前關註的唯一核心指標，如訂單數，交易額等。不同的關註會導致公司戰略上的不同。
   
3. 第三確定指標後，需要確定描述主體 。同樣是房價，政府說我們今年有60%的城市，房均價比去年低！你們買房有希望了！但實際上，40%的房子都漲價了，且都集中在核心城市。P 民們照樣買不起房子..
   
4. 註意時代背景 ：【赤裸裸的統計學】中舉了個很有趣的例子：如何評價歷史上票房最高的電影。好萊塢在截止2011年時，給出的票房前 5 名是：阿凡達，鐵達尼號，蝙蝠俠前傳二，星際大戰四和怪物史萊克二。但歷史階段上，通脹情況是不一樣的。把通脹因素考慮進來後，這個榜單應該更新為：亂世佳人，星際大戰四，音樂之聲，外星人 ET 和十誡。
   
5. 利用統計學手段可以影響人們的解讀：截取有利時間段，混淆單位等。
   

陷阱 三：統計指標也有偏見

在選擇樣本和進行統計分析時，會存在各種各樣的偏見，導致結果失之毫厘，謬以千裏。

1. 選擇性偏見 ：選擇了錯誤的樣本，得到的分析結論自然是錯的。如在第三季矽谷裏，Richard 對自己的開發者朋友們釋出了 Beta 版，好評如潮。但因為其上手難度太高，普通使用者根本用不了。最後導致註冊使用者雖有百萬之巨，但活躍使用者卻寥寥無幾。同樣的，在對電商使用者習慣做分析時，一二線城市和三四線城市的消費水平糊習慣肯定有所差異，選擇任一種都會有失偏頗。
   
2. 發表性偏見 ：學術研究或新聞更樂於發表肯定性結論而非否定性。一個打遊戲不會引發癌癥的研究，肯定不如證明當 PM 會導致壽命更短的實驗更受關註。
   
3. 記憶性偏見 ：人們會因為結果修改自己的記憶，如很多成功人士會在失敗後將原因歸咎於某個因素，並將其放大成關鍵原因。但事實上可能並非如此。
   
4. 幸存者偏見 ：透過挑選樣本來操控數據。簡而言之，對於那些下單成功的使用者數來講，他們的註冊成功率是 100%。在日常分析中，需要時刻警惕這種偏見的變異版本。

陷阱 四：慎重選擇統計實驗

在研究事物的相關性時，透過控制變量實驗來研究是個比較科學的做法。在現實生活中，一些變量很難甚至無法控制，此時便需透過各種統計實驗來逼近這種效果。

1. 隨機控制實驗 ：隨機抽取樣本，隨機分配實驗組和對照組。這便是最理想的 A/B Test，核心在分桶策略。
   
2. 自然實驗 ：利用已有數據營造近似的隨機實驗，如在 O2O 城市營運中，很難長期控制城市去做實驗要求的推廣活動來對比哪種活動比較有效。合適的方法是從已有的數據中，挑選情況類似活動不同的城市來進行對比分析。
   
3. 差分類差分實驗 ：利用時間和空間上的對比來控制變量，如美國曾經研究過受教育年齡對壽命的影響，就可以研究了田納西州在教育改革時間前後的變化，以及和相鄰州對比情況。
   
4. 非連續分析實驗 ：選擇條件類似但治療條件不同，進行對比分析。如選擇一批犯罪情況類似，但一批需要送去監獄一批剛好免除牢獄之災的兩組人進行對比分析，來研究坐牢對青年人後續犯罪率的影響。

高端技能的使用：回歸分析

在統計分析過程中，會遇到從多個變量中判斷相關性的過程。此時，統計學的大殺器「回歸分析」便閃亮登場。

1. 回歸分析可以給出精確的答案，卻不一定正確。如上世紀 90 年代風行一時的雌激素補充療法，醫療依據是由哈佛醫學院主持發現了女性身體健康與雌性激素的相關性。後來透過臨床試驗被證偽，但據估計，這個療法已經導致了上萬人過早離世。
   
2. 7個常見錯誤：用回歸過程分析非線性關系（如高爾夫成績與課程多少，並不是線性相依或根本不相關），相關並非因果，倒果為因，忽略核心變量（如高爾夫患病機率高，其實只是因為年紀大的人才有時間打），高度相關的解釋變量（需要精簡和合並，如吸食海洛因和可卡因），數據礦（變量過多），脫離數據進行推斷（要明確可使用的樣本範圍）
   
3. 回歸分析註意項：設計一個好的回歸方程式，明確變量和收集方式；以樣本為立足點，需要能對所用變量作出解釋

4 參考

1. https:// coffee.pmcaff.com/artic le/414504464258176/
2. http://www. woshipm.com/data-analys is/4195180.html
3. http://www. woshipm.com/data-analys is/5170018.html