選自arXiv,作者:Iddo Drori等,機器之心編譯,機器之心編輯部。
前段時間,DeepMind 的一項研究登上【Nature】封面,透過引導直覺解決了兩大數學難題;之後,OpenAI 教 GPT-3 學會了上網,能夠使用基於文本的 Web 瀏覽器。
就在 2021 年的最後一天, MIT 與哥倫比亞大學、哈佛大學、滑鐵盧大學的聯合研究團隊發表了一篇長達 114 頁的論文,提出了首個可以大規模自動解決、評分和生成大學水平數學問題的模型,可以說是人工智能和高等教育的一個重要裏程碑。其實在這項研究之前,人們普遍認為神經網絡無法解決高等數學問題。
值得一提的是,該研究用到了 OpenAI 的 Codex。
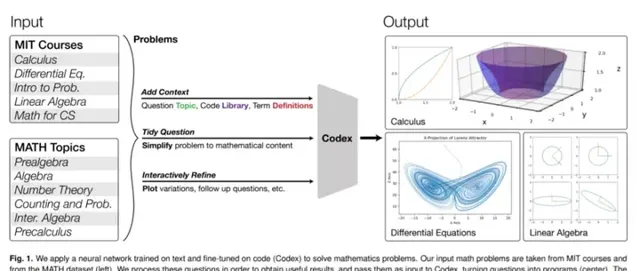
這項研究有多厲害呢?我們以下圖為例,下圖展示了計算勞侖次吸子及其投影,計算和演示奇異值分解 (SVD) 方法的幾何形狀等。機器學習模型很難解決上述問題,但這項研究表明它們不僅可以解決這些問題,還可以大規模解決所屬課程以及許多此類課程問題。
該研究表明對文本進行預訓練並在程式碼上進行微調的神經網絡,可以透過程式合成(program synthesis)解決數學問題。具體而言,該研究可將數學問題轉化為編程任務,自動生成程式,然後執行,以解決 MIT 數學課程問題和來自 MATH 數據集的問題。其中,MATH 數據集是專門用於評估數學推理的高等數學問題最新基準,涵蓋初級代數、代數、計數與概率、數論與微積分。
此外,該研究還探索了一些提示(prompt)生成方法,使 Transformer 能夠為相應主題生成問題解決程式,包括帶有影像的解決方案。透過量化原始問題和轉換後的提示之間的差距,該研究評估了生成問題的質素和難度。

論文地址:https:// arxiv.org/pdf/2112.1559 4.pdf
方法
數據集
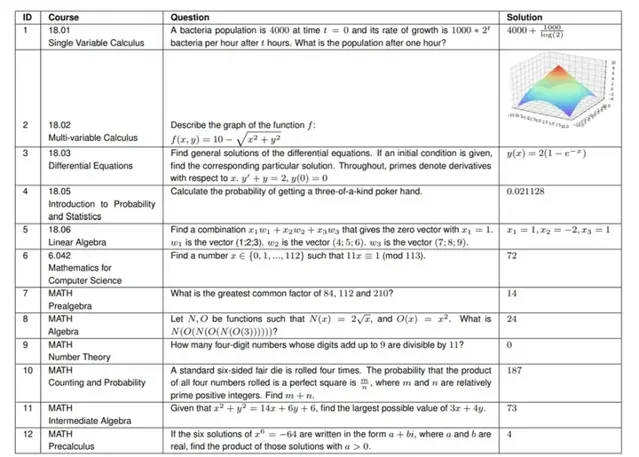
該研究首先從 MIT 的以下六門課程中,每門課程隨機選取了 25 個問題:
對於 MATH 數據集,該研究從每個主題中隨機抽取 5 個問題,並透過在套用線性代數新課程 COMS3251 上的實驗驗證了該方法的結果不僅僅是過擬合訓練數據。
方法流程
如下圖 2 所示,該研究使用 Codex 將課程問題轉換為編程任務並運行程式以解決數學問題。下圖共包含 A-E 5 個面板,每個面板的左側部份顯示了原始問題和重新表述的提示,其中提示是透過添加上下文、互動、簡化描述等形成的。
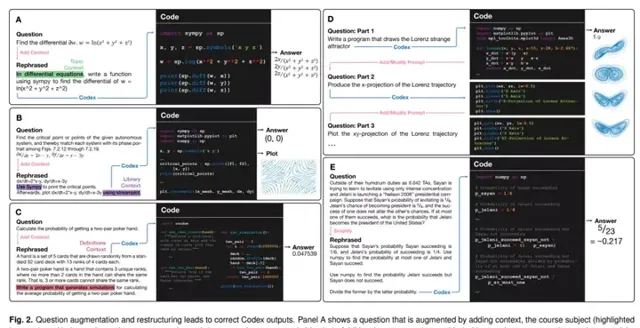
該研究將從原始課程問題到 Codex 提示的轉換分為以下三類:
問題與提示之間的差距
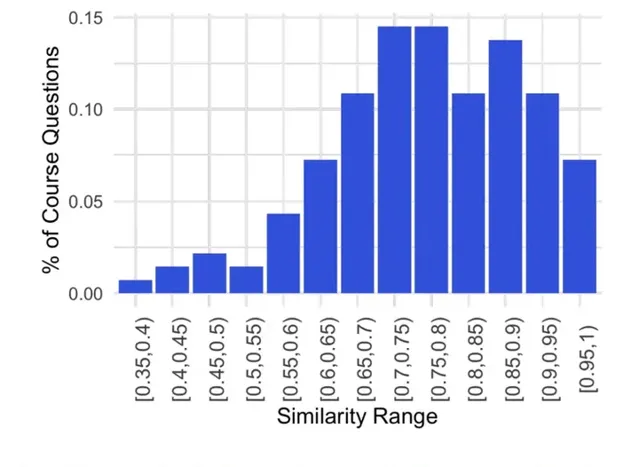
將問題轉換為 Codex 提示的關鍵是:從語意上講,原始問題與產生正確解決方案的提示之間的接近程度。為了度量原始問題和成功提示之間的差距,該研究使用 Sentence-BERT 嵌入之間的余弦相似度,如下圖 3 所示。
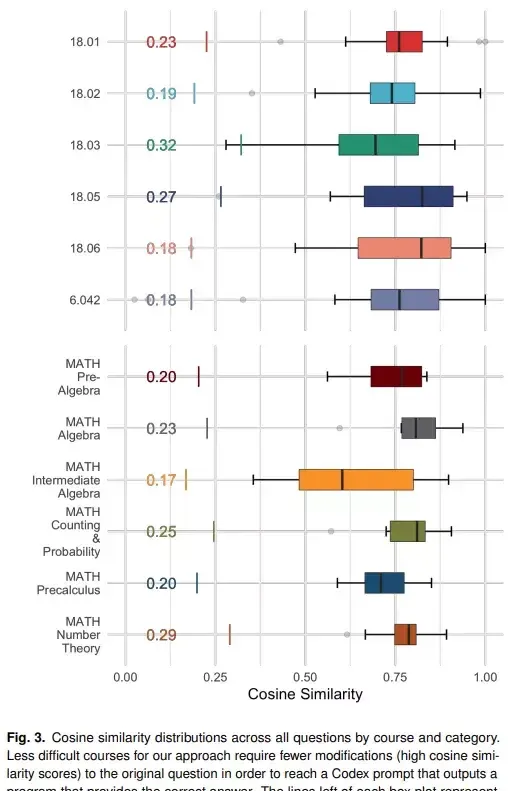
Sentence-BERT 使用 siamese 和 triplet 神經網絡結構對預訓練的 BERT 模型進行微調。其中至關重要的是,Sentence-BERT 能夠在句子級別生成語意嵌入,從而可以在長文本之間進行語意相似性比較。
在該研究的實驗中,原始問題和生成正確答案的提示之間的相似度如下圖 4 所示。
Codex 用於提示生成
在某些課程中,直接使用未轉換的原始問題提示 Codex,無法產生正確的解決方案。因此,需要將原始問題轉化為 Codex 可以處理的形式,主要分為以下三類:
生成問題以及人類評估
該研究使用 Codex 為每門課程生成新的問題,透過數據集建立有編號的問題列表來完成,這個列表在生成隨機數量的問題之後會被截斷斷,結果將用於提示 Codex 生成下一個問題。不斷的重復這個過程,就可以為每門課程產生許多新的問題。
該研究對參加過這些課程或同等課程的、來自 MIT 和哥倫比亞大學的學生進行了一項長期調查。 調查的目的是比較每門課程機器生成的問題與人工編寫的問題的質素和難度 。該研究為每門 MIT 的課程隨機抽取五個原始問題和五個生成的問題。在調查中,學生被要求閱讀每門課程的十個問題,這些問題是人工編寫的問題和機器生成的問題的混合。
對於 60 個問題中的每一個,學生都被問到三個問題,如圖 5 所示:他們是否認為給定的問題是 (i) 人工編寫的或機器生成的,(ii) 適合或不適合特定課程,以及 (iii) ) 在 1(最簡單)和 5(最難)之間的範圍內,問題的難度級別是多少。要求學生提供他們對數學問題的評分,而不是解決這些問題。該調查以線上和匿名的形式提供。

調研結果
問題求解
研究者共求解了補充資料中展示的 210 個問題,其中包括 6 門課程各自對應的 25 個隨機問題以及 MATH 數據集中 6 個主題(初級代數、代數、數論、計數與概率、中極代數、微積分)各自對應的 10 個隨機問題。
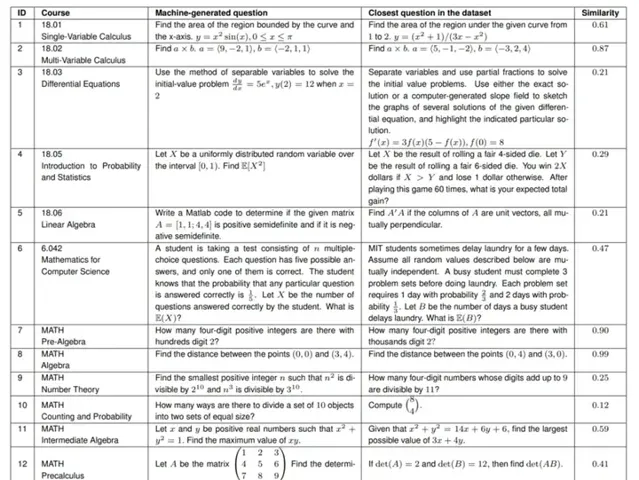
生成新問題
研究者生成了 120 個新問題,其中包括 6 門課程和 6 個 MATH 主題各自對應的 10 個新問題。下表 2 展示了每門課程和每個 MATH 主題對應的一個生成問題。生成一個問題只需不到 1 秒的時間,研究者可以生成任意數量的問題。他們為 Codex 能夠生成正確答案的 25 個隨機選擇的問題建立了提示,切入隨機問題,並讓 Codex 完成下一個新問題。
學生調研結果
研究者表示,共有 13 位參與者完成了全部 60 個問題的問答調研,平均耗時 40 分鐘。下圖 6 總結了學生調研中人工編寫(human-written)和機器生成(machine-generated)問題的比較情況,並得出了以下幾項結果:
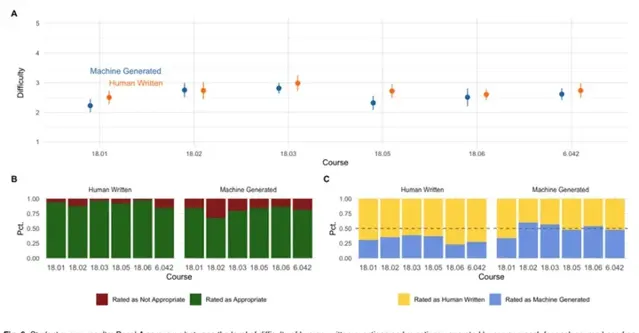
答案定級
Codex 能夠回答所有隨機采樣的大學水平糊 MATH 數據集數學問題,無論它們是原始狀態還是整理後狀態。
挑戰
研究者的方法還有一些無法解決的技術障礙。
1、輸入影像。Codex 的一個基礎限制是它只能接收基於文本的輸入。因此,Codex 無法使用圖形或圖表等必要的視覺元件來回答問題。
2、高等數學證明。這項研究的另一個限制是缺乏對高等數學的證明。研究者強調稱,這是由研究自身的廣度而不是 Codex 的證明能力導致的。事實上,該研究中送出至 Codex 的大多數簡單分析證明都已成功地被執行,這令人震驚,因為證明通常不是基於程式碼的。
3、程式評估。該研究的最後一步是執行程式,例如使用 Python 直譯器。參加大學水平課程的學生也會編寫程式碼來解決他們的部份問題。因此,該研究以與人類學生相同的方式測試神經網絡解決問題的能力,讓他們使用必要的工具。還有關於神經程式評估的工作,演示了使用機器學習來預測程式輸出。LSTM 用於成功預測某些線性時間和恒定空間程式的輸出 (18)。這些都增加了記憶體暫存器以允許更大的程式類別 (19)。最近的方法使用因果 GNN (20) 和 transformer (21)。盡管評估任意程式碼是不可判定的,但特殊情況,例如由另一個 transformer 生成的用於解決簡單數學問題的程式,原則上應該是可學習的。
4、理論復雜性。計算復雜度的結果表明,該研究無法解決大學數學課程中一般問題的每一個具體例項。例如,以下問題具有難以處理的結果:向量 v 可以表示為來自集合 S 的向量之和嗎?以下一階微分方程式的解是什麽?但是,我們知道作業和考試給出的問題可以由人類解決,因此這些復雜性結果不適用於該研究的特定例項解決。











