來來來,題主,就按照你的思路,咱們來算一下唄!
首先,為了便於理解,我們挑一個最簡單的圖形,就比如 \[y = {x^2}\] 吧。
我們來試著計算一下該函數在區間 \[\left[ {0,1} \right]\] 上的影像與 x 軸所圍成的面積,即下圖陰影部份面積:
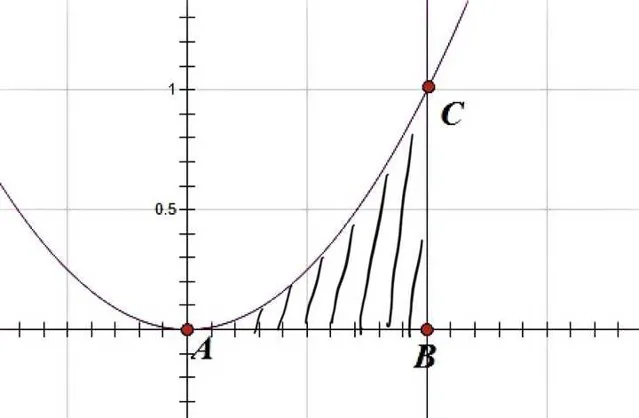
為了方便起見,就假設它的面積等於 S 吧,咱們接下來就是想辦法把 S 的具體數值給算出來。
好,接下來咱們就用題主說的細矩形來逼近,第一次我們將區間\[\left[ {0,1} \right]\] 分割成兩部份,分別是 \[\left[ {0,\frac{1}{2}} \right]\] 與 \[\left[ {\frac{1}{2},1} \right]\] 。
那如何確定矩形呢?我們采用的分割方法是,以 區間內二次函數的最小值為矩形的高 。
在區間\[\left[ {0,\frac{1}{2}} \right]\] 內,\[y = {x^2}\] 的最小值在 \[x = 0\] 處取得,此時 y=0 ,故此時矩形的高為 0 。
在區間\[\left[ {\frac{1}{2},1} \right]\] 內,\[y = {x^2}\] 的最小值在 \[x = {\frac{1}{2}}\] 處取得,此時 \[y={\left( {\frac{1}{2}} \right)^2}\] ,故此時矩形的高為 \[{\left( {\frac{1}{2}} \right)^2}\] 。
如下圖所示,不過因為第一個矩形的高為 0 ,所以在圖上無法看出,但讀者在心裏應該看到下圖有兩個矩形:

這兩個矩形的面積之和為多少呢?
我們用 \[{a_2}\] 表示這兩個矩形的面積之和,那應該有:
\[{a_2}\]
\[ = \frac{1}{2} \times {0^2} + \frac{1}{2} \times {\left( {\frac{1}{2}} \right)^2}\]
\[ = \frac{1}{2}\left[ {{0^2} + {{\left( {\frac{1}{2}} \right)}^2}} \right]\]
\[ = \frac{1}{{{2^3}}}\left( {{0^2} + {1^2}} \right)\]
應該看到,因為這兩個矩形都完全的在二次曲線的內部,即這兩個矩形的面積必然是要小於 S 的,所以我們有: \[{a_2} \le S\] 。
接下來,我們繼續分割,將區間\[\left[ {0,1} \right]\] 分割成三部份,即: \[\left[ {0,\frac{1}{3}} \right]\] , \[\left[ {\frac{1}{3},\frac{2}{3}} \right]\] , \[\left[ {\frac{2}{3},1} \right]\] 。
接著確定矩形,套路還是一樣的,以 區間內二次函數的最小值為矩形的高 。
在區間\[\left[ {0,\frac{1}{3}} \right]\] 內,\[y = {x^2}\] 的最小值在 \[x = 0\] 處取得,此時 y=0 ,故此時矩形的高為 0 。
在區間\[\left[ {\frac{1}{3},\frac{2}{3}} \right]\] 內,此時矩形的高為 \[{\left( {\frac{1}{3}} \right)^2}\] 。
在區間\[\left[ {\frac{2}{3},1} \right]\] 內,矩形的高為 \[{\left( {\frac{2}{3}} \right)^2}\] 。
還是要註意,下圖看上去只有兩個矩形,但讀者的心裏應該明白有三個矩形,第一個矩形只是因為它的高為 0 所以無法畫出,但並不意味著它不存在。
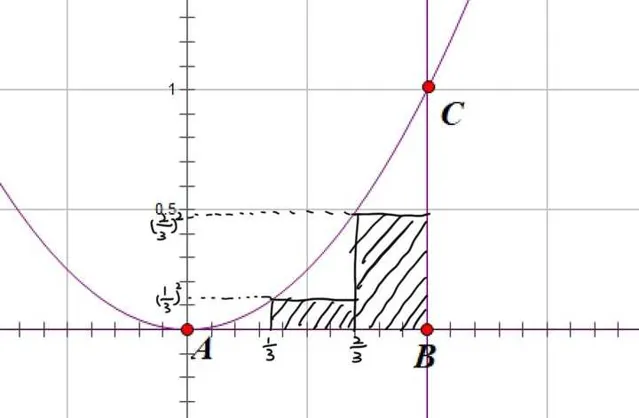
我們用 \[{a_3}\] 表示這三個矩形的面積之和,還是一樣的:
\[{a_3}\]
\[ = \frac{1}{3} \times {0^2} + \frac{1}{3} \times {\left( {\frac{1}{3}} \right)^2} + \frac{1}{3} \times {\left( {\frac{2}{3}} \right)^2}\]
\[ = \frac{1}{{{3^3}}}\left( {{0^2} + {1^2} + {2^2}} \right)\]
且這三個矩形也是在二次曲線之下,故有: \[{a_3} \le S\] 。
最後我們再試試將區間\[\left[ {0,1} \right]\] 分割成四部份的形式,此時會有四個矩形:

則 \[{a_4} = \frac{1}{{{4^3}}}\left( {{0^2} + {1^2} + {2^2} + {3^2}} \right)\] ,且 \[{a_4} \le S\] 。
按照這種劃分方法,我們很容易得到,當我們將區間 n 等分時, n 個矩形的面積之和為:
\[{a_n} = \frac{1}{{{n^3}}}\left( {{0^2} + {1^2} + \cdots + {(n-1)^2}} \right)\]
且 \[{a_n} \le S\] 。
我們再算一下當 \[{n \to +\infty }\] 時的情形,即
\[\mathop {\lim }\limits_{n \to \infty } {a_n} = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}}\left[ {{0^2} + {1^2} + \cdots + {{\left( {n - 1} \right)}^2}} \right]\]
我們有公式 \[{1^2} + {2^2} + \cdots + {n^2} = \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\]
將 n-1 代入,我們有: \[{1^2} + {2^2} + \cdots + {\left( {n - 1} \right)^2} = \frac{{\left( {n - 1} \right)n\left( {2n - 1} \right)}}{6}\]
故: \[\mathop {\lim }\limits_{n \to \infty } {a_n}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}}\left[ {{0^2} + {1^2} + \cdots + {{\left( {n - 1} \right)}^2}} \right]\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}} \cdot \frac{{\left( {n - 1} \right)n\left( {2n - 1} \right)}}{6}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot \frac{{\left( {n - 1} \right)n\left( {2n - 1} \right)}}{{{n^3}}}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot \frac{{n - 1}}{n} \cdot \frac{n}{n} \cdot \frac{{2n - 1}}{n}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot \left( {1 - \frac{1}{n}} \right) \cdot 1 \cdot \left( {2 - \frac{1}{n}} \right)\]
\[ = \frac{1}{3}\]
所以最後我們得到: \[\frac{1}{3} = \mathop {\lim }\limits_{n \to \infty } {a_n} \le S\]
題主的意思就是,既然每次劃分的時候,矩形的面積之和一直小於 S ,那你憑什麽認為最後 S 的面積就是 a_n 的極限?
別著急,接下來我們再看一種劃分方法!
這次還是先將區間\[\left[ {0,1} \right]\] 分割成兩部份,分別是 \[\left[ {0,\frac{1}{2}} \right]\] 與 \[\left[ {\frac{1}{2},1} \right]\] 。
但我們如何確定矩形呢?這次采用的分割方法是,以區間內二次函數的 最大值 為矩形的高。
在區間\[\left[ {0,\frac{1}{2}} \right]\] 內,\[y = {x^2}\] 的最大值在 \[x = {\frac{1}{2}}\] 處取得,此時 \[y={\left( {\frac{1}{2}} \right)^2}\] ,故此時矩形的高為 \[{\left( {\frac{1}{2}} \right)^2}\] 。
在區間\[\left[ {\frac{1}{2},1} \right]\] 內,\[y = {x^2}\] 的最大值在 \[x =1\] 處取得,此時 y=1^2 ,故此時矩形的高為 1^2 。
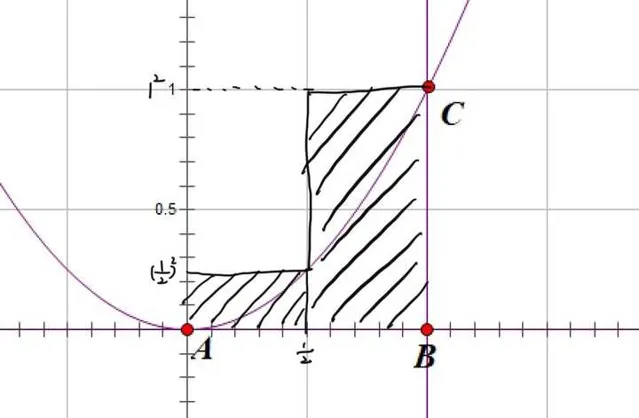
這兩個矩形的面積之和為多少呢?
我們用 \[{b_2}\] 表示這兩個矩形的面積之和,那應該有:
\[{b_2}\]
\[ = \frac{1}{2} \times {\left( {\frac{1}{2}} \right)^2} + \frac{1}{2} \times {1^2}\]
\[ = \frac{1}{2}\left[ { {{\left( {\frac{1}{2}} \right)}^2}} +{1^2} \right]\]
\[ = \frac{1}{{{2^3}}}\left( { {1^2}} +{2^2} \right)\]
應該看到,這次這兩個矩形完完全全的覆蓋了二次曲線,所以這兩個矩形的面積必然是要大於 S 的,所以我們有: \[S \le {b_2}\] 。
我們繼續分割,將區間\[\left[ {0,1} \right]\] 分割成三部份,即: \[\left[ {0,\frac{1}{3}} \right]\] , \[\left[ {\frac{1}{3},\frac{2}{3}} \right]\] , \[\left[ {\frac{2}{3},1} \right]\] 。
接著確定矩形,套路還是一樣的,以區間內二次函數的 最大值 為矩形的高。
這三個區間矩形的高分別為: \[{\left( {\frac{1}{3}} \right)^2}\] , \[{\left( {\frac{2}{3}} \right)^2}\] , 1^2 。
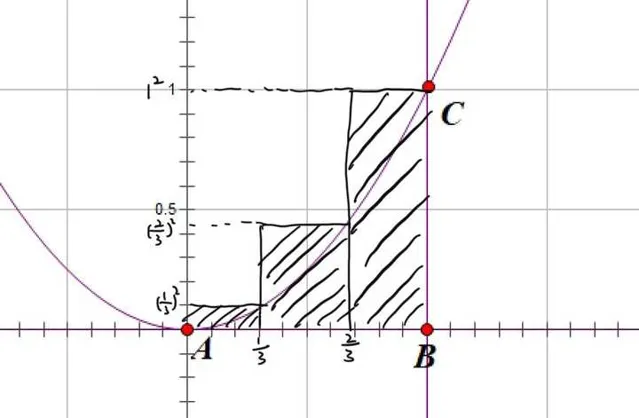
然後 \[{b_3}\]
\[ = \frac{1}{3} \times {\left( {\frac{1}{3}} \right)^2} + \frac{1}{3} \times {\left( {\frac{2}{3}} \right)^2} + \frac{1}{3} \times {1^2}\]
\[ = \frac{1}{{{3^3}}}\left( {{1^2} + {2^2} + {3^2}} \right)\]
且 \[S \le {b_3}\]
最後,我們依照下圖,計算一下 b_4
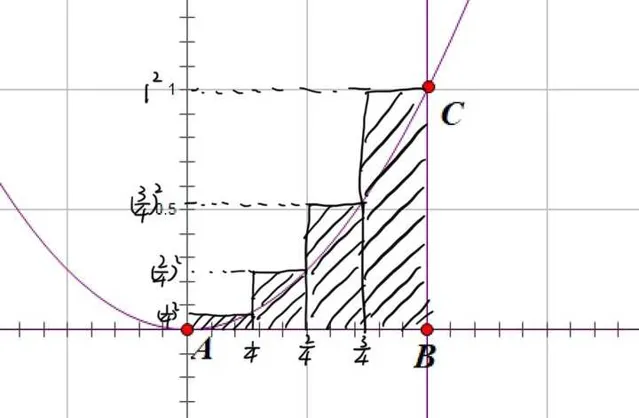
\[{b_4}\]
\[ = \frac{1}{4}\left[ {{{\left( {\frac{1}{4}} \right)}^2} + {{\left( {\frac{2}{4}} \right)}^2} + {{\left( {\frac{3}{4}} \right)}^2} + {1^2}} \right]\]
\[ = \frac{1}{{{4^3}}}\left( {{1^2} + {2^2} + {3^2} + {4^2}} \right)\]
最後,我們很容易的得到了這種劃分方式的通項公式,即: \[{b_n} = \frac{1}{{{n^3}}}\left( {{1^2} + {2^2} + \cdots + {n^2}} \right)\]
又因為這種劃分下,這些細矩形是可以覆蓋掉整個二次曲線圍成的圖案的,故 \[S \le {b_n}\]
最後再計算一下 b_n 的極限,
即 \[\mathop {\lim }\limits_{n \to \infty } {b_n}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}}\left( {{1^2} + {2^2} + \cdots + {n^2}} \right)\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}} \cdot \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot 1 \cdot \left( {1 + \frac{1}{n}} \right) \cdot \left( {2 + \frac{1}{n}} \right)\]
\[ = \frac{1}{3}\]
而我們又有 \[S \le \mathop {\lim }\limits_{n \to \infty } {b_n} = \frac{1}{3}\]
而我們之前又有\[\frac{1}{3} = \mathop {\lim }\limits_{n \to \infty } {a_n} \le S\] ,透過夾逼定理,我們得到了 S 是真的等於 \[\frac{1}{3}\] ,換句話說,用細矩形面積的和逼近時,隨著劃分的越來越細,誤差是趨近於 0 的。
好的問題會對數學的進步產生推動作用,題主無疑提了一個很好的問題,那順著這個思路,我們有哪些思考方向呢?
首先是這篇回答我簡單的說了一下兩種劃分方法,分別是取區間內函數的最大值與最小值作為矩形的高,最後發現當 \[{n \to +\infty }\] 時,就不存在誤差了。
這件事其實暗含了極限理論的基本思想,極限到底是什麽?是指兩個數很近很近嗎?
而如果將這種劃分思路一般化,在數學裏我們將其稱為 達布上和 與 達布下和 。
自然的,在這個二次函數的例子裏我們發現最終的結果是達布上和等於達布下和,事實上,有許多函數都滿足這一性質,我們將這些函數稱為黎曼可積的
那是否存在一些函數,它的達布上下和不相等呢?
有的,這種情況下我們將其稱為黎曼不可積
最後,在這篇文章中,我們劃分的是 x 軸,那請問有沒有劃分 y 軸的方法呢?
也是有的,我們將其稱為勒貝格積分……
好吧,我們已經說的夠遠了,就此打住吧。











