之前解答有錯誤,在此訂正一下。直接將暴力寫出所有約束條件,使用幾何概型概率模型計算。
原問題轉為數學問題如下:
x+y+z=1, x, y, z\geq 0
求 \mathbb{E}_x[x],\ s.t. x\leq y, z
更一般地: x_1+x_2+\cdots+x_n=1, x_i\geq 0
求 \mathbb{E}_{x_1}[x_1], \ s.t. x_1 \leq x_2, \cdots, x_n
在滿足得到任意 (x_1, x_2, \cdots, x_n) 等概率的條件下(忽略材料因素引起的斷裂可能性偏差) ,此概率問題可視作幾何概型概率問題,求解滿足條件區域的體積占比即可。對一般情況,
總概率空間為 \Omega=\{(x_1, x_2, x_3, \cdots, x_n)|0\leq x_1\leq x_2, x_3, \cdots, x_n\leq 1\}
該概率空間可進一步轉化為以下不等式組決定的 n-1 維空間:
\begin{equation} \left\{ \begin{array}{lr} x_i\geq 0, i=2, 3, \cdots, n \\ x_2+\cdots+x_n\leq 1 \\ 2x_2+x_3+\cdots+x_n\geq 1, \ (x_2\geq x_1) \\ x_2 + 2x_3 + \cdots+x_n \geq 1, \ (x_3\geq x_1) \\ \vdots \\ x_2+x_3+\cdots+2x_n \geq 1, \ (x_n\geq x_1) \\ \end{array} \right. \end{equation}
其中前兩個為已知條件,後面 n-1 個不等式保證每個元素都不小於 x_1 。
考慮事件 A=x_1\geq a , 此時事件 A 的概率空間由以下不等式組決定,只需把第二個不等式進一步約束為x_2+\cdots+x_n\leq 1-a 即可。由此事件 A 對應的空間 \Omega_A 由以下不等式決定:
\begin{equation} \left\{ \begin{array}{lr} x_i\geq 0, i=2, 3, \cdots, n \\ x_2+\cdots+x_n\leq 1-a \\ 2x_2+x_3+\cdots+x_n\geq 1, \ (x_2\geq x_1) \\ x_2 + 2x_3 + \cdots+x_n \geq 1, \ (x_3\geq x_1) \\ \vdots \\ x_2+x_3+\cdots+2x_n \geq 1, \ (x_n\geq x_1) \\ \end{array} \right. \end{equation}
對於 n=3 , 如下圖所示。 y+2z=1, 2y+z=1, y+z=1 三條直線圍成的區域 \Delta{ABC} 表示 x+y+z=1, x\leq y, z 。 y+2z=1, 2y+z=1, y+z=1-a 圍成的區域 \Delta ADE 表示在 x 最小的情況下, x\geq a 對應的區域。兩個區域公共頂點為 (\frac13, \frac13) ,其面積比代表了概率 P(x_1\geq a) 。面積比可利用 \frac{S_{ADE}}{S_{ABC}}=(\frac{x_D-x_A}{x_B-x_A})^2=(\frac{1-2a-1/3}{1-1/3})^2=(1-3a)^2 得到。
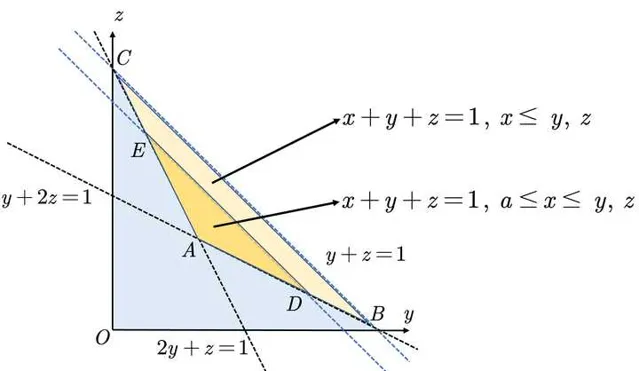
一般情況下, \Omega 對應的錐體與 \Omega_A 的錐體共頂點 (\frac1n, \frac1n, \cdots, \frac1n) ,錐體體積可由座標比值得到。具體地,考慮使用 x_2 對應維度的座標,其座標值(對應上圖 D 點的橫座標)由以下方程式組決定:
\begin{equation} \left\{ \begin{array}{lr} x_2+\cdots+x_n= 1-a \\ x_2+2x_3 + x_4+\cdots+x_n=1 \\ x_2 + x_3 + 2x_4 + \cdots+x_n =1 \\ \vdots \\ x_2+x_3+x_4\cdots+2x_n =1\\ \end{array} \right. \end{equation}
容易求得此時的座標值為 x_2=1-(n-1)a (對應上圖的 D 點橫座標)。因此錐體體積比值為: \frac{|\Omega_A|}{|\Omega|}=(\frac{1-(n-1)a-1/n}{1-1/n})^{n-1}=(1-na)^{n-1}=P(x_1\geq a) ,
於是有 P(x_1<a)=1-(1-na)^{n-1} ,進而求得概率密度 p(x_1)=P'=n(n-1)(1-nx_1)^{n-2}
從而 \mathbb{E}_{x_1}[x_1]=\int_{0}^{1/n}x_1p(x_1)dx_1=n(n-1)\int_{0}^{1/n}x_1(1-nx_1)^{n-2}dx_1
積分 \begin{align} \int x(1-nx)^{n-2}dx&=-\frac{1}{n(n-1)}\int x d\{(1-nx)^{n-1}\} \\ &=-\frac{1}{n(n-1)}x(1-nx)^{n-1}+\frac{1}{n(n-1)}\int(1-nx)^{n-1}dx \\ &=-\frac{1}{n(n-1)}x(1-nx)^{n-1}-\frac{1}{n^3(n-1)}(1-nx)^n \end{align}
因此即可得到 \mathbb{E}_{x_1}[x_1]=n(n-1)\frac{1}{n^3(n-1)}=\frac1{n^2} ,即最短的一段平均值為 \frac1{n^2} 。











