貝葉斯濾波相關可參考:zzg:機器人演算法基礎:貝葉斯濾波 , 也可以先閱讀此文,遇到貝葉斯相關再去參考
數據融合
平均值融合
使用同一台電子稱 , 對一個物體進行兩次測量 ,得到兩次測量結果A , B ,如下圖所示
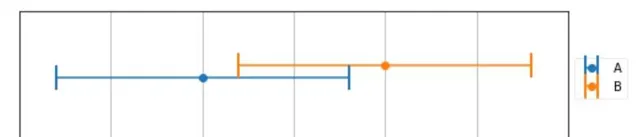
圖中用線段表示測量結果而不是點 表明稱不是絕對精準的 , 它有一個誤差範圍 +- 8 kg ,假設在這個範圍內 , 可能性都是相同(符合均勻分布,實際上正態分布更合理,但是這裏重點不是什麽類別的分布),那麽我們如何選擇最終的測量結果呢?
按照常識我們會對兩次結果求平均值 :
M = \frac {A+B} 2\\
在圖中,平均值表示得區域 為重疊部份得中點 165
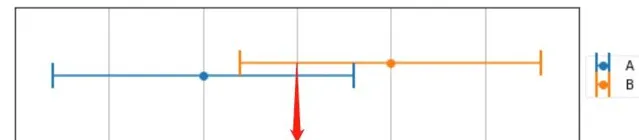
將上面得計算公式變形,可以更加直觀的理解:
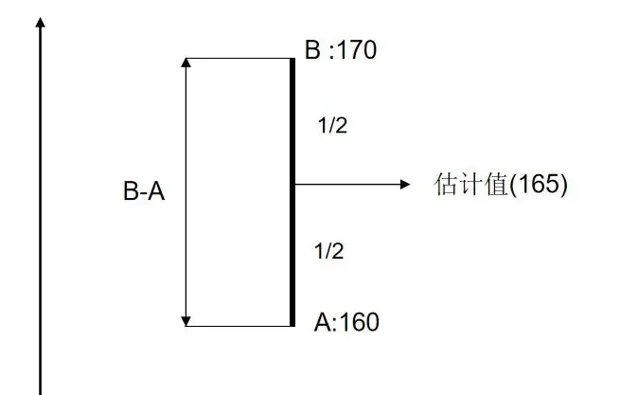
M=\frac {A+B} {2} = \frac {A+A+B-A}{2} = A + \frac{B-A}{2}\\
M的結果為 A 加上 AB之間的差值的 一半 , 為何這裏剛好選 一半? 因為兩次的測量結果來自同一台稱 , 我們沒有理由更加傾向於 A, 或者B 。
加權平均融合
使用兩台精度不同的稱 來稱同一物體,得到 了測量結果如下圖所示
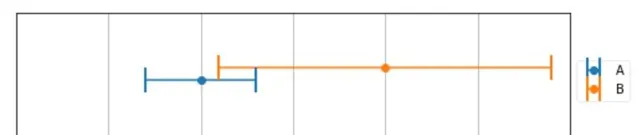
可以很明顯的看到 , A 測量精度明顯高於 B 的精度,這個時候我們該如何選則測量結果呢? 還是求平均值嗎,得到165 的結果?
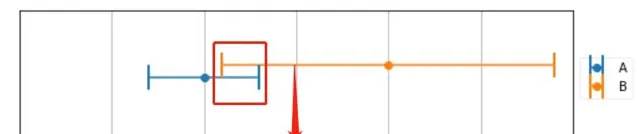
這不符合我們的直觀。首先, 真實的結果應該同時滿足在兩個稱的測量結果範圍內 , 如圖重合部份。至於在重合部份的具體那個地方,我們做一個數值假設:
A 測量結果 為 160 +- 3
B 測量結果 為 170 +- 9
在使用同一個傳感器測量時,我們對兩次測量結果的傾向性相同 , 各占 1/2 。在這裏A 的測量結果精度是 B 測量結果精度的 3倍 ,我們會產生這樣的直觀 , 根據精度比例 , 我們 \frac 3 4 傾向 A 測量結果 , \frac 1 4 傾向 B結果。
M = \frac 3 4 A + \frac 1 4 B = A+ \frac{1}{4} (B-A) = 161\\
可以看到計算結果在上圖中重合部份 , 且滿足 了 A 精度是 B 精度的 3 倍這個條件 , 這就是加權平均,A的測量值權重為 \frac 3 4 , B測量值的權重為 \frac 1 4 , 權重 總和 為 1.
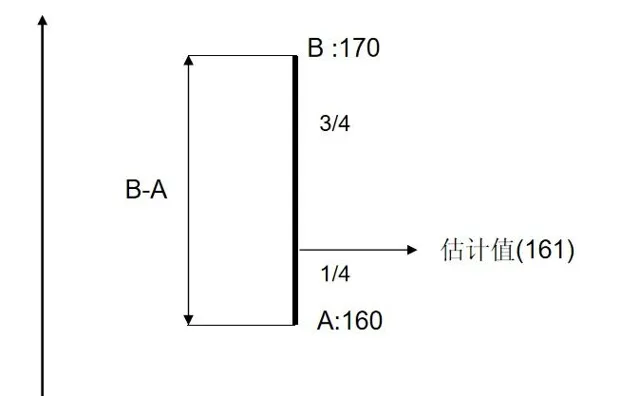
直觀上,加權平均基本能說服我們 ,按這種方法得到的估計是最優估計,那有沒有理論證明呢?
最優狀態估計
在開始證明前 ,我們需要一些期望代數的背景知識 ,如果了解可直接跳過
期望代數
平均值與期望
對於隨機變量 x , E(x) = \mu_x , 也就是隨機變量的期望 , 等於其平均值。
若隨機變量 x 符合概率 分布 P(x) , 則
若 P(x) 離散:
E(x) = \sum xp(x)\\
若 P(x) 連續:
E(x) = \int xp(x)dx\\
變異數和標準差
變異數用來度量隨機變量與其期望值(即隨機變量的期望值)之間的離散程度。
標準差是變異數的平方根。標準差: \sigma ,變異數: \sigma^2
例如,我們想比較兩個高中籃球隊的身高。下表提供了兩支球隊的球員身高及其平均值。

如我們所見,兩隊的平均身高是一樣的。現在讓我們檢查一下高度變化變異數。由於變異數用來度量隨機變量與其期望值(即隨機變量的期望值)之間的離散程度,我們想知道數據集偏離其平均值的情況。我們可以透過從每個變量中減去平均值來計算每個變量與平均值之間的距離。我們將用x表示高度,用希臘字母μ表示高度的平均值。每個變量與平均值的距離為:
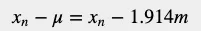
下表給出了每個變量與平均值之間的距離。

下表給出了每個變量與平均值的平方距離。有些值是負數。為了消除負值影響,讓我們將高度與平均值的距離平方:
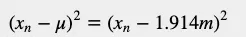

為了計算數據集的離散程度,我們需要從中找出所有平方距離的平均值:
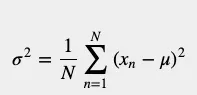
A隊的變異數是:

B隊的變異數是:

我們可以看出,雖然兩隊的平均值相同,但A隊的身高分布值高於B隊的身高分布值,這意味著A隊在控球員、中鋒和後衛等不同位置有不同的球員,而B隊球員則技能相差無幾。變異數的單位是平方的;檢視標準差更方便。正如我已經提到的,標準差是變異數的平方根。

A隊運動員身高的標準差為0.12米。
B隊運動員身高的標準差為0.036米。
進一步的,現在,假設我們要計算所有高中籃球運動員的平均值和變異數。這是一項非常艱巨的任務,我們需要收集所有高中運動員的數據。
但是,我們可以透過選擇一個大的數據集並對這個數據集進行計算來估計參與者的平均值和變異數。(樣本估計全域)
隨機選取的100名選手的數據集足以進行準確的估計。
然而,當我們 估計變異數 時,變異數計算公式略有不同。我們不用N因子歸一化,而是用因子歸一化:
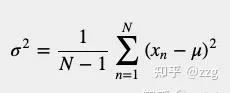
你可以在以下資源中看到這個方程式的數學證明:[http://www. visiondummy.com/2014/03 /divide-variance-n-1/ ](
期望代數公式
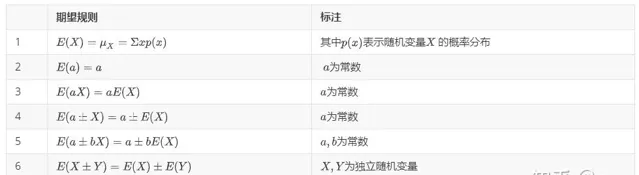

後文中需要用到的公式有:
最優狀態估計推導
兩個獨立的變量 x_1 , x_2 ( x_1 , x_2 為兩個精度不同的稱稱量同一物體得到得測量值), 變異數分別為 \sigma_1^2 , \sigma_2^2 ,我們透過加權平均來做估計有:
\hat x = w_1x_1 + w_2x_2\\ w_1+w_2 = 1
其中為 x_1 的權重 w_1 , x_2 為 w_2 的權重 , 根據變異數得計算公式可得:
\sigma_1^2 = E((x_1-E(x_1))^2)\\ \sigma_2^2 = E((x_2-E(x_2))^2)
估計值 \hat x 的期望為:
E(\hat x) = E(w_1x_1+w_2x_2) \\ = E(w_1x_1)+E(w_2x_2)\\ =w_1E(x_1)+w_2E(x_2)
估計值 \hat x 的變異數為:
\begin{align} \sigma^2 &= E((\hat x - E(\hat x))^2)\\ &= E((w_1x_1+w_2x_2-w_1E(x_1)-w_2E(x_2))^2)\\ &= E(((w_1(x_1-E(x_1)) + w_2(x_2-E(x_2)))^2)\\ &= E(w_1^2(x_1-E(x_1))^2 + w_2^2(x_2-E(x_2))^2 + 2w_1w_2(x_1-E(x_1)(x_2-E(x_2)))\\ & = w_1^2E((x_1-E(x_1))^2) +w_2^2E((x_2-E(x_2))^2) + 2w_1w_2COV(x_1,x_2) \\ & = w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2COV(x1,x2) \end{align}
由於 x_1 , x_2 是獨立的 ,所以 x_1 , x_2 的共變異數 COV(x_1 , x_2) = 0 , 則:
\sigma^2 = w_1^2\sigma_1^2 + w_2^2\sigma_2^2\\
由 w_1 + w_2 = 1 可設 w_2 = w , w_1= 1-w , 代入上式可得:
\sigma^2 = (1-w)^2\sigma_1^2 + w^2\sigma_2^2\\
最優估計,即是讓估計的變異數 \sigma^2 最小 , 這樣估計得結果就更精確 , 上式中,唯一的變量是 w , 因此需要求使得 \sigma^2 最小的 w 值,觀察函數 , 發現是一元二次方程式,開口向上 , 存在最小值 , 透過求導 ,令導數等於0 得到最小值。
\begin{align} \frac {d_{\sigma^2}}{d_w} &= 2(w-1)\sigma_1^2 + 2w\sigma_2^2 = 0\\ w &= \frac {\sigma_1^2}{\sigma_1^2 + \sigma_2^2} \end{align}\\
將 w 的 值 帶入 \sigma^2 的 計算公式中, 得到:
\begin{align} \sigma^2 &= (1-w)^2\sigma_1^2 + w^2\sigma_2^2 \\ &= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} = w\sigma_2^2 = (1-w)\sigma_1^2 \end{align}\\
因此,最優狀態估計:
\begin{align} \hat x &= (1-w)x_1 + wx_2 = \frac {\sigma_2^2x_1 + \sigma_1^2x_2}{\sigma_1^2 + \sigma_2^2} \\ \sigma^2 &= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{align}\\
以上推導完畢。
我們驗證一下先前兩台不同精度的稱 是否 符合 最優狀態估計。已知 :
A的測量結果 x_1=160 , 標準差 \sigma_1 = 3
B的測量結果 x_2 = 170 , 標準差 \sigma_2 = 9
按照最優估計公式計算 , 最優估計:
\begin{align} \hat x &= \frac {9^2*160 + 3^2*170}{3^2 + 9^2} = 161 \\ \sigma^2 &= \frac{3^2*9^2}{3^2+9^2} = 8.1 \end{align}\\
結果與我們的直觀 估計相同。
在貝葉斯章節,我們知道,兩個高斯分布相乘, 其結果為高斯函數。,觀察高斯函數相乘的結果可以發現,與最優估計的結果相同,因此可以得出結論: 符合高斯分布的貝葉斯濾波(先驗和似然均是高斯分布)得到的後驗是最優狀態估計,而後面的卡爾曼濾波就是基於高斯分布和貝葉斯的,所以卡爾曼濾波屬於最優狀態估計的一類濾波器 。
X\sim N(\mu_x , \sigma_X^2)\\ Y\sim N(\mu_y , \sigma_Y^2)\\ \mu = \frac {\sigma_x^2\mu_y+\sigma_y^2\mu_x} {\sigma_x^2+ \sigma_y^2}\\ \sigma^2 = \frac {\sigma_x^2\sigma_y^2} {\sigma_x^2+\sigma_y^2}
g—h濾波器
在前面的章節中 , 我們主要介紹了如何將兩個傳感器的數據進行融合 , 並進行最優估計的方法。那假設我們只有一個傳感器呢 ,有沒有辦法做類似的估計呢 , 在貝葉斯章節 , 我們經常提到先驗概率 , 這個概率在測量之前就有了 , 我們根據先驗概率和測量之後得到的似然概率得到後驗 。 那麽有沒有一種辦法,在我們還未進行測量前 , 就得到 一個大概的預測, 然後用這個預測和測量值按照上面的步驟,做最優估計呢?
狀態外推方程式
我們可以透過物理規律 , 對觀測物體進行預測,比如運動的物體 , 我們需要對它的位移進行估計 , 在進行測量前,我們可以運用牛頓運動方程式推導下一一時刻物體的位置:
\begin{align} x_{predict} &= \hat x + \hat v\Delta t + \frac{1}{2}\hat a\Delta t^2\\ v_{predict} &= \hat v + \hat a\Delta t\\ a_{predict} &= \hat a + f(\Delta t) \end{align}\\
其中, \hat x 表示當前時刻對位移的估計 , x_{predict} 表示下一時刻的位移,是一個預測值(還未發生) , \Delta t 表示時間步長(離散的) , f(\Delta t) 表示加速度隨時間變化,這樣就可以表示任意狀態的運動。類似上面的式子被稱為,狀態外推方程式。
狀態更新方程式
得到了預測值後我們進行測量 , 然後將 預測值 和 測量值 進行加權平均 ,也就是:
\begin{align} \hat x &= (1-w) x_{predict} + wx_{z}\\ &= x_{predict} + w(x_z-x_{predict}) \end{align}\\
我們在最優狀態規估計中知道了如何選擇 w ,得到最優狀態估計 , 但是有的系統可能我們沒法得知變異數,也就無法 計算 w 值,有個簡單的辦法,將w值 作為一個定值 ,透過調整 w 的值,讓估計值整體變得更合理, 這種方法稱為數值法,透過大量的數據,調整w 得到最優估計(類似的演算法還有PID,透過數據整定PID參數)。 將 w 改成 g ( 有的地方也稱為 \alpha ) ,就得到了 g-h 濾波器 的狀態更新 方程式:
\begin{align} \hat x &= x_{predict} + g(x_z-x_{predict})\\ \hat v &= v_{predict} + h(\frac{x_z-x_{predict}}{\Delta t})\\ \hat a &= a_{predict} + k(\frac{x_z-x_{predict}}{0.5\Delta t^2}) \end{align}\\
其中: (x_z-x_{predict}) 稱為殘留誤差 , 解釋為一個 時間步長 , 測量值與預測值的差值 , 透過下圖理解 , 即為藍色點減去紅色點的值。對速度的預測,只需將位移殘留誤差除以時間步長(位移的一階導數得到速度)即可。加速度是位移的二階導,因此,可以得到上面3個狀態更新方程式。

g-h濾波器的工作步驟
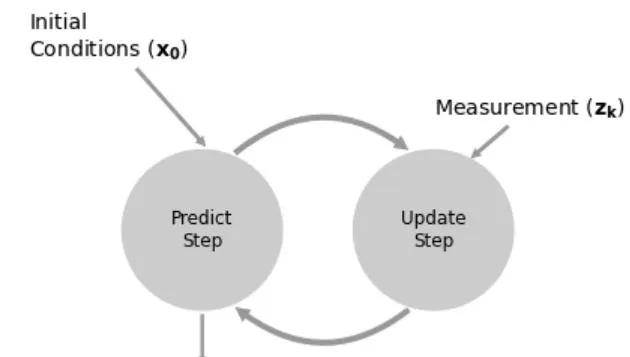
上圖表示了g-h濾波器的工作流程。
這種預測和更新的叠代模式有效的 減小了數值的儲存問題 , 我們只需要關註當前值,和預測值 ,而不需要考慮過去的歷史值 , 如果濾波器表現良好,最終的估計值將慢慢收斂到真實值。下面我們透過幾個具體的範例來說明 g-h 濾波器。
範例一:追蹤一維勻速飛行器
現在,來看一個隨時間改變狀態的動態系統吧。在這個例子中,我們用 g-h 濾波器 在一維空間中追蹤勻速飛行的飛行器。
假設在一個一維空間,有一架飛行器正在向遠離雷達(或朝向雷達)的方向飛行。在一維空間中,雷達的角度不變,飛行器的高度不變,如下圖所示。
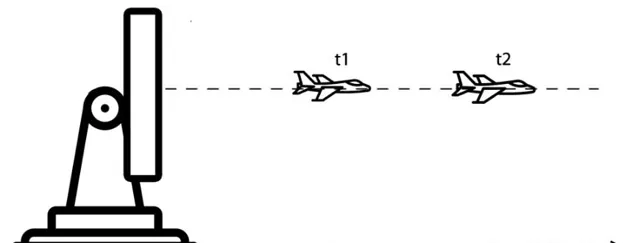
x_n 代表飛行器在 n 時的航程。飛行器速度定義為航程相對於時間的變化率,即為距離的導數:
\dot x = v = \frac {d_x}{d_t}\\
雷達以恒定頻率向目標方向發射追蹤波束,周期為 \Delta t 假設飛行器速度恒定,系統的動態模型可以用兩個運動方程式來描述:
\begin{align} x_{n+1 ,n} &= \hat x_{n,n} + \hat{\dot x}_{n,n}\Delta t\\ \dot x_{n+1,n} &= \hat{\dot x}_{n,n} \end{align}\\
由於需要進行數值叠代,這裏將下標改成和 n 相關的,n表示叠代的次數 , 用 \hat{} 表示是估計值,也就是我們關註的經過預測值和測量值融合的結果 ,上式中各項的含義:
上述方程式即上面提到的 用於預測的狀態外推方程式,我們的狀態更新方程式如下:
\hat x_{n,n} = x_{n,n-1} + g(z_n-x_{n,n-1})\\ \hat {\dot x}_{n,n} = \dot x_{n,n-1} + h(\frac{z_n-x_{n,n-1}}{\Delta t})\\
上式各項的含義:
上面對 n 的設定很合理 n+1 表示將來的,也就是預測 , n 表示當前的 ,也就是當前估計 , n-1 表示之前的,結合 x_{n,n-1} , 則表示n-1 時對 n 的預測。
思考: 為什麽追蹤勻速的飛行器還需要在狀態更新方程式裏面增加對速度的估計?它不是勻速的嗎 ?也就是下面的式子。
\hat {\dot x}_{n,n} = \dot x_{n,n-1} + h(\frac{z_n-x_{n,n-1}}{\Delta t})\\
確實, 對於測量系統 , 已經知道了飛行器是勻速的 ,所以在狀態外推方程式中,我們進行預測一直是將飛行當成勻速的:
\begin{align} x_{n+1 ,n} &= \hat x_{n,n} + \hat{\dot x}_{n,n}\Delta t\\ \dot x_{n+1,n} &= \hat{\dot x}_{n,n} \end{align}\\
但是這個勻速的速度是多少呢?雷達是不知道的 , 要知道的話就不用進行測量了,我們的預測是100%準確的。雷達只能測距離,透過一個時間步長的位移差來計算當前速度:
\frac{z_n-x_{n,n-1}}{\Delta t}\\
但是,雷達的測量是誤差的,這就導致對速度的估計產生了誤差,所以每個時間步長對速度的估計都會不同,但在同一個時間步長裏還是認為它是勻速的。
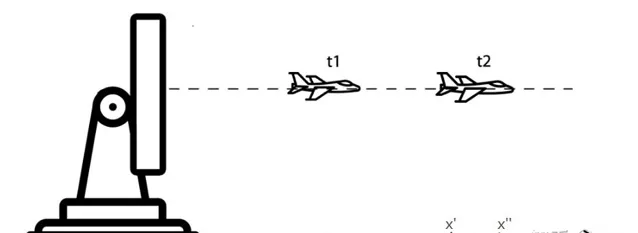
數值案例
g-h濾波器參數
設定g-h濾波器的 參數 :
g = 0.2 , h =0.1\\
至於為什麽這麽多,可以考慮 g 表示是 位移測量值的權重,這說明我們更加相信預測值 , h表示速度測量值的權重,同樣更相信預測值,因為我們已經知道系統是勻速的。雷達每5s ,測量一次 , 也就是時間步長:
\Delta t = 5s\\
第0次叠代:
\begin{align} \hat x_{0,0} &= 30000m \\ \hat{\dot x}_{0,0} &= 40m/s \end{align}\\
將數值代入狀態外推方程式,計算下一時刻位移和速度:
\begin{align} x_{1 ,0} &= \hat x_{0,0} + \hat{\dot x}_{0,0}\Delta t = 30000 + 40*5 = 30200m\\ \dot x_{1,0} &= \hat{\dot x}_{0,0} = 40m/s \end{align}\\
第1次叠代:
y_1 = 30110m\\
進行估計:
\begin{align} \hat x_{1,1} &= x_{1,0} + g(y_1-x_{1,0}) = 30200+0.2(30110-30200) = 30182m \\ \hat {\dot x}_{1,1} &= \dot x_{1,0} + h(\frac{y_1-x_{1,0}}{\Delta t}) = 40+0.1(\frac{30110-30200}{5}) = 38.2m/s\\ \end{align}\\
\begin{align} x_{2 ,1} &= \hat x_{1,1} + \hat{\dot x}_{1,1}\Delta t = 30182 + 38.2*5 = 30373m\\ \dot x_{2,1} &= \hat{\dot x}_{1,1} = 38.2m/s \end{align}\\
經過10次叠代後 , 得到下表 , 將下表繪制成折線圖
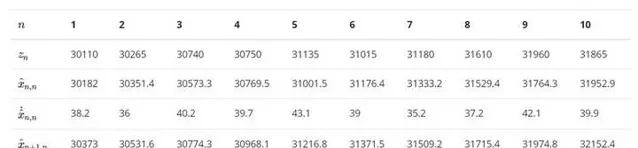
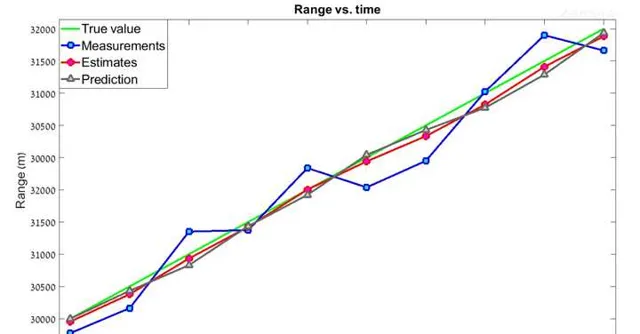
可以看到,估計值比測量值更加平滑 , 而且更加靠近真實值。如果使用更高的 g-h 值呢? g=0.8 , h = 0.5 , 這表明我們更加相信測量值
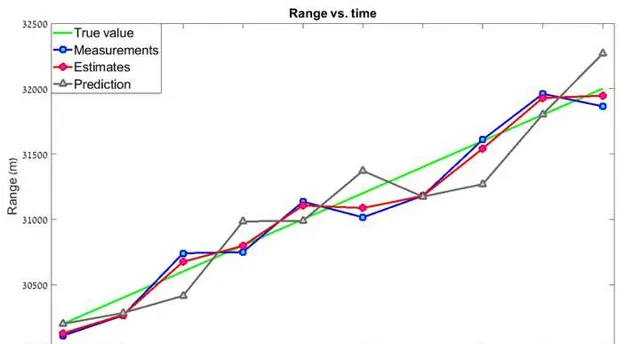
這個濾波器的「平滑度」要低得多,「當前估計值」與測量值非常接近,預測誤差較大。那麽我們應該一直選擇低的 gh 嗎?答案是否定的。 gh 的值取決於測量精度。如果我們使用非常精準的器材,比如激光雷達,我們會傾向高 gh ,測量值權重更高,在這種情況下,濾波器會對目標的速度變化作出快速響應。反之,如果測量精度較低,我們會選擇較低 gh , 在這種情況下,濾波器將降低測量中的不確定性(誤差),然而,濾波器對目標速度變化的反應會慢得多。
範例二:追蹤一維勻加速飛行器
如果直接直接用追蹤勻速飛行的 g-h濾波器來最終勻加速會發生什麽?我們在勻速系統中使用的過程模型,或者說狀態外推方程式是
\begin{align} x_{n+1 ,n} &= \hat x_{n,n} + \hat{\dot x}_{n,n}\Delta t\\ \dot x_{n+1,n} &= \hat{\dot x}_{n,n} \end{align}\\
預測下一時刻的速度不變,但實際情況是勻加速的,而我們設定的 g-h參數(0.2 ,0.1)明顯是更相信預測值的。因此最終濾波器應該會產生滯後,我們用數值案例來看最終的結果。飛行器的運動情況如下圖所示,在0-15 勻速運動,在15-50 勻加速運動。
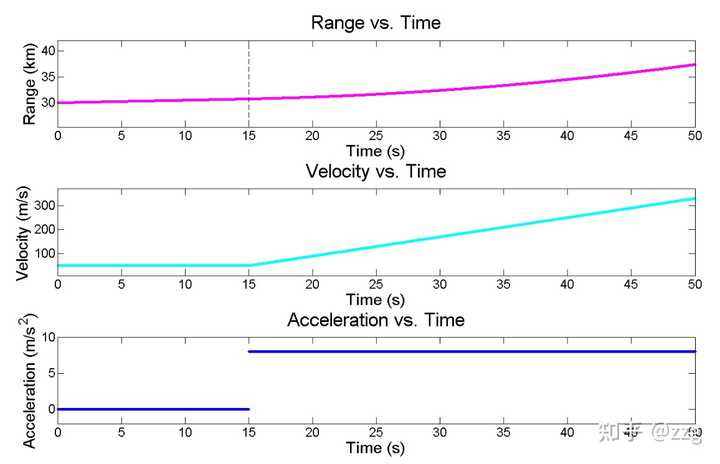



可以看到真實值或測量值與估計值之間存在一個固定的差值,這個差值被稱為 滯後誤差lag error 。滯後誤差的其他常見名稱有:
我們更正系統模型 , 為系統增加加速度 , 因此狀態外推方程式如下:
\begin{align} x_{n+1 ,n} &= \hat x_{n,n} + \hat{\dot x}_{n,n}\Delta t + \frac{1}{2} \hat{\ddot x}_{n,n} \Delta t^2\\ \dot x_{n+1,n} &= \hat{\dot x}_{n,n} + \hat{\ddot x}_{n,n}\Delta t\\ \ddot x_{n+1,n} &= \hat{\ddot x}_{n,n} \end{align}\\
式子中,速度用位移的一階導數表示 : \hat{\dot x}_{n,n} , 加速度用位移的二階導表示 : \hat{\ddot x}_{n,n} 狀態更新方程式我們增加對加速度的估計:
\begin{align} \hat x_{n,n} &= x_{n,n-1} + g(z_n-x_{n,n-1})\\ \hat {\dot x}_{n,n} &= \dot x_{n,n-1} + h(\frac{z_n-x_{n,n-1}}{\Delta t})\\ \hat {\ddot x}_{n,n} &= \ddot x_{n,n-1} + k(\frac{z_n-x_{n,n-1}}{0.5\Delta t^2})\\ \end{align}\\
經過數值案例叠代,最終得到的曲線如下圖所示:
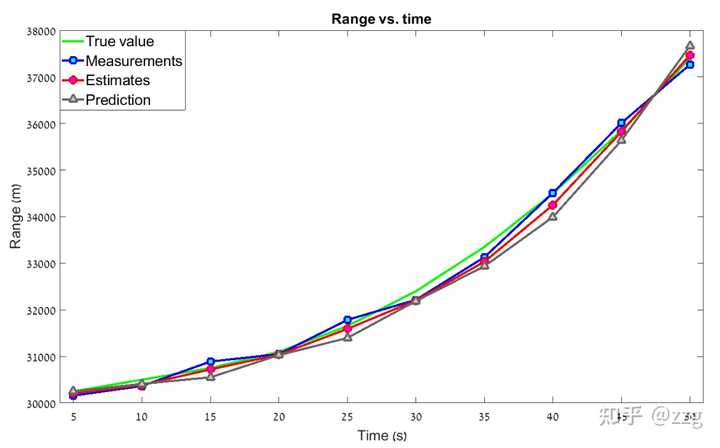
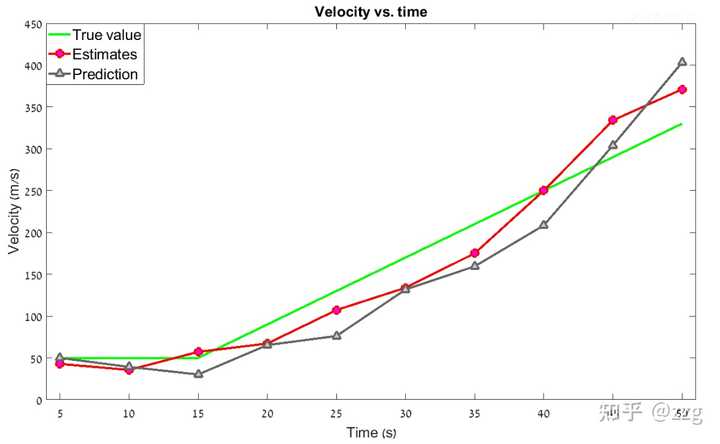
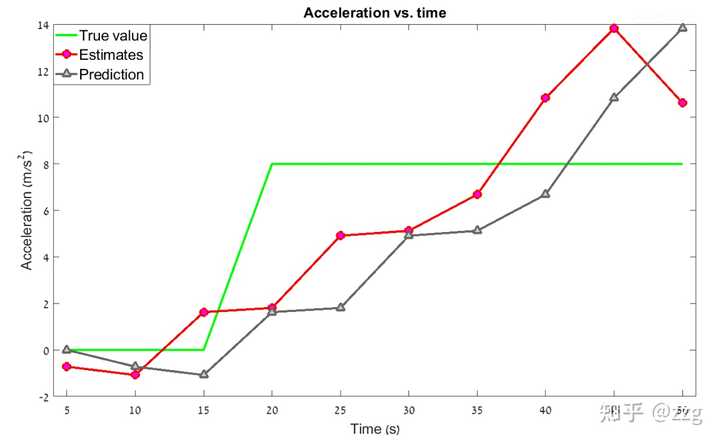
如圖所見,包含加速度動態模型的 g-h-k 濾波器可以追蹤勻加速運動的目標,並且消除滯後誤差。但是如果目標的運動狀態是高度變化的呢?目標可以透過轉彎突然改變飛行方向,真實的目標動態模型可能包括一個突然加速(改變加速度),在這些情況下,具有恒定 g-h-k 系數的 g-h-k 濾波器會產生估計誤差,在某些情況下甚至會追蹤失效。
通用g-h濾波器Python實作
import numpy as np
def g_h_filter(zdata, x0, dx, g, h, dt=1.):
x_est = x0 #初始化的估計值
results = []
for z in zdata:
# prediction step
x_pred = x_est + (dx*dt)
dx = dx
# update step
residual = z - x_pred #殘留誤差
dx = dx + h * (residual) / dt
x_est = x_pred + g * residual
results.append(x_est)
return np.array(results)
這裏 dx 表示 x 的變化率 , 是一個抽象的變量 , 我們前面的粒子就是速度,當然這裏也可以增加x的二階導數。 對於一個動態系統,可以用狀態的多階導數來表示,這一點在後面多維卡爾曼濾波中會介紹。
g-h參數調節
g是系統測量值的權重,需要根據傳感器的精度和系統模型的精度共同來確定 , 比如你對系統模型不那麽確定, 大致上是勻速,可能會有小的擾動,而傳感器的精度很高,那就選擇較高的g 值, h反應的系統狀態變化的測量值權重 , 可以發現,h越大過濾器越靈敏 , 但太過靈敏可能導致濾波器過分偏向測量值,或者錯誤值。
g-h濾波器與卡爾曼濾波器的聯系
看到這裏,你可能會覺得,接下來終於可以學習卡爾曼濾波了。但其實 ,卡爾曼濾波 的 5個方程式我們前面已經都使用過了,並且證明了它的由來 , 你知道是哪幾個嗎?如果沒有深刻的印象 , 可以回過頭再去看看貝葉斯濾波 和 上文。
g-h濾波器和卡爾曼濾波器有什麽聯系?我們知道g-h 濾波器的參數是透過 數值進行調整,從而得到適合參數,這種前提意味著,當系統變化較大時,有需要重新調節g-h 參數 ,才能達到理想的效果。就拿前面勻速和勻加速的例子來說,系統模型不可能這麽完美 , 有時會出現大振幅的變化,比如突然轉向,這個時候我們的g-h參數已經不太適合當前的變化了,就需要動態調整了,怎麽去動態調整呢?這就是卡爾曼濾波做的事了。
我們在最優狀態估計的證明中,提到了如何設定 g-h 值達到 最優估計 , 但是由於上面的例子沒有引入概率(期望和變異數),導致無法計算,只能透過數值叠代,來觀察曲線,調整g-h 達到理想值。而卡爾曼濾波在g-h濾波器的基礎上,引入概率,從而得到了最優狀態估計。
假設你不知道有卡爾曼濾波,能否根據下面的一些啟發推匯出來?(體驗一下卡爾曼老爺子是如何將兩者關聯起來的)
g-h濾波器給我們的啟發
\begin{align} \hat x &= (1-w)x_1 + wx_2 = \frac {\sigma_2^2x_1 + \sigma_1^2x_2}{\sigma_1^2 + \sigma_2^2} \\ \sigma^2 &= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{align}\\

貝葉斯濾波高斯分布給我們的啟發
\begin{align} X \sim& N(\mu_X , \sigma_X^2)\\ Y \sim& N(\mu_Y , \sigma_Y^2)\\ Z =& X+Y \end{align}\\
則
\begin{align} Z \sim N(\mu_X+\mu_Y , \sigma_X^2 + \sigma_Y^2) \end{align}\\
X\sim N(\mu_x , \sigma_X^2)\\ Y\sim N(\mu_y , \sigma_Y^2)\\
則
\mu = \frac {\sigma_x^2\mu_y+\sigma_y^2\mu_x} {\sigma_x^2+ \sigma_y^2}\\ \sigma^2 = \frac {\sigma_x^2\sigma_y^2} {\sigma_x^2+\sigma_y^2}\\
\begin{align} P(post) =& \frac{P(Z|prior)P(prior)} {P(Z)}\\ =& \frac{\mathcal N(\mu_z, \sigma_z^2)*\mathcal N(\mu_p ,\sigma_p^2)}{Normal}\\ =& \mathcal N(\frac {\sigma_z^2\mu_p+\sigma_p^2\mu_z} {\sigma_z^2+ \sigma_p^2} , \frac {\sigma_z^2\sigma_p^2} {\sigma_z^2+\sigma_p^2})/Normal \end{align}\\
我們的後驗估計結果:
\begin{align} \hat x &= \frac {\sigma_z^2\mu_p+\sigma_p^2\mu_z} {\sigma_z^2+ \sigma_p^2} \\ \sigma^2 &= \frac {\sigma_z^2\sigma_p^2} {\sigma_z^2+\sigma_p^2} \end{align}\\
結合兩者得到卡爾曼濾波
\begin{align} x_{n+1 ,n} &= \hat x_{n,n} + \hat{\dot x}_{n,n}\Delta t \space\space \space\space \space\space\space\space (1) \\ \end{align}\\
進行預測 , 這裏有很重要的一點,估計值 \hat x_{n,n} , \hat{\dot x}_{n,n} 符合高斯分布 , \Delta t 是常數 , 因此 狀態外推方程式是2個高斯函數相加 , 根據高斯函數的特點 ,結果仍為高斯函數,設狀態變量的估計值的變異數為 P , 狀態變量的變化量的估計值變異數為 \Delta P ,則可得到:
P_{n+1 , n} = P_{n,n} + \Delta P_{n,n}\\
這就是卡爾曼濾波方程式的 : 共變異數外推方程式,至於為什麽叫共變異數而不是變異數,是因為在多維的情況下,變量與變量之間還有關系,而且期望代數中可知,變異數是共變異數的特例。 共變異數外推方程式計算的是預測值的變異數 , 或者說不確定度。往往更一般的形式會在預測中加入雜訊,雜訊的變異數為Q , 則
\begin{align} x_{n+1 ,n} &= \hat x_{n,n} + \hat{\dot x}_{n,n}\Delta t +w\\ P_{n+1 , n} &= P_{n,n} + \Delta P_{n,n} + Q \space\space\space\space\space\space\space\space(2) \end{align}\\
我們已經得到了兩個卡爾曼濾波方程式 : 狀態外推方程式 , 共變異數外推方程式 ,到這裏還只是運用了g-h 濾波器 和 高斯分布的加法特性 , 還沒有結合貝葉斯濾波,很明顯,貝葉斯濾波是在更新的過程中使用的。
我們學習了兩種數據融合的方法,最終形成估計的方法, 一種是g-h 濾波器,加權平均進行更新 , 令一種是貝葉斯濾波 ,結合先驗和測量得到後驗。既然引入了概率 , 那麽我更加希望使用貝葉斯濾波,我們在之前有見識過概率的力量 :我們得到的估計值有一個精度可以參考 , 比如溫度 是95℃+-0.1 。而g-h濾波器呢 , 只有一個估計值,沒有精度資訊。但是按照g-h 濾波器使用加權平均方法 , 我們可以得到最優狀態估計,前面也證明這一點 , 因此我們在引入概率後,可以從兩個方面 來得到卡爾曼濾波方程式。由g-h濾波器 的最優狀態估計得到 , 由貝葉斯濾波方法得到。
g-h濾波器最佳化角度得到:
最佳化更新方程式由前面證明得:
\begin{align} \hat x &= x_1 + w(x_2-x_1) = \frac {\sigma_2^2x_1 + \sigma_1^2x_2}{\sigma_1^2 + \sigma_2^2} \space\space\space\space\space\space\space\space(3)\\ \sigma^2 &= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \end{align}\\
我們令 :
K_n = w = \frac {\sigma_1^2}{\sigma_1^2 + \sigma_2^2}\\
K_n 稱為卡爾曼增益 ,其實就是先前的g , 只不過在g-h濾波器中 , g 是定值 , 而這裏得卡爾曼增益是一個變值,其中 \sigma_1 ,\sigma_2 具體是預測變異數和測量變異數(因為 x_1 和x_2 這裏具體指的是預測值 和測量值 , 由共變異數外推方程式可得到預測值變異數 , 測量變異數可根據傳感器參數得到為 R , 則:
K_n = \frac {P_{n ,n-1}}{P_{n,n-1} + R_n} \space\space\space\space\space\space\space\space(4)\\
估計值的變異數用 K_n 來表示:
P_{n,n} =\sigma^2 = \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} = (1-K_n)P_{n,n-1}\space\space\space\space\space\space\space\space(5)\\
以上5個公式即為卡爾曼濾波公式 , 2個預測 , 2個更新 , 一個卡爾曼濾波增益。
從貝葉斯濾波的角度得到:
在預測步驟中 , 我們 透過狀態外推方程式和共變異數外推方程式得到了預測值 , 和預測值的變異數 , 且由高斯函數的加法特性得知,預測值也是高斯函數。這個預測值在貝葉斯濾波中我們稱為先驗 , 表示出來 就是:
X_{predict} \sim \mathcal N(\mu_p ,\sigma_p^2)\\
經過測量後,得到測量值符合高斯分布 :
R \sim \mathcal N(\mu_z ,\sigma_z^2)\\
透過貝葉斯公式我們得到後驗估計值:
\begin{align}3P(post) =& \frac{P(Z|prior)P(prior)} {P(Z)}\\4=& \frac{\mathcal N(\mu_z, \sigma_z^2)*\mathcal N(\mu_p ,\sigma_p^2)}{Normal}\\5=& \mathcal N(\frac {\sigma_z^2\mu_p+\sigma_p^2\mu_z} {\sigma_z^2+ \sigma_p^2} , \frac {\sigma_z^2\sigma_p^2} {\sigma_z^2+\sigma_p^2})/Normal\end{align}\\
可以觀察到,最終的估計值,有一個不可思議的巧合。對比g-h 濾波器推匯出的 加權平均最優估計的結果 , 會發現驚人的相同 。 估計值和變異數 都一樣,很好奇當時卡爾曼老爺子到底是為什麽選擇高斯分布 ? 是從g-h濾波器最優估計得到卡爾曼濾波方程式的還是先透過貝葉斯濾波得到估計值 , 然後發現居然結果和g-h濾波器的最優狀態估計結果相同的?
到這裏,相信已經能夠理解卡爾曼濾波和貝葉斯濾波 ,g-h濾波的關系了。 卡爾曼濾波 基礎主要是 3大塊 , 貝葉斯 , 高斯 , g-h 濾波器。如果還不能理解,建議反復閱讀讀懂的章節。
下節預告:一階線性卡爾曼濾波
主要說套用相關,以及為何上述的卡爾曼濾波只能線上性系統中使用 , 若是非線性的系統會造成什麽 , 什麽情況下會引入非線性。
參考資料
https://www. kalmanfilter.net/defaul t.aspx
https:// github.com/rlabbe/Kalma n-and-Bayesian-Filters-in-Python










