空间索引（k

2021-12-10知识

最近研究了一下kd-tree，并且用python实现了，代码见文末链接。

kd-tree是k-dimensional tree的缩写，主要用来做空间索引，包括范围搜索和最近邻搜索，2分查找树可以看做是kd-tree在一维情况下的一个特例。

构造K-d tree

2分查找树是对1维数据做分类索引，但扩展到2维的情况下就不太适用。例如要查找距离(2, 3)最近的点，如果只根据x的值进行2分查找可能会得到错误的结果，因为距离还和y的值有关。这时候就需要用到kd-tree，对x和y 2个维度做划分。

kd-tree的构造过程是交替的根据当前数据的不同维度进行切分，例如假设为2维度数据(x,y)，root节点先根据x轴进行划分，得到左右2个部分，然后再分别对左右2个部分根据y轴进行划分，依次进行，直到划分的区域内只有一个节点。以下是2维K-d tree的示意图，同理可以扩展到N维度空间。

2维空间的K-d tree

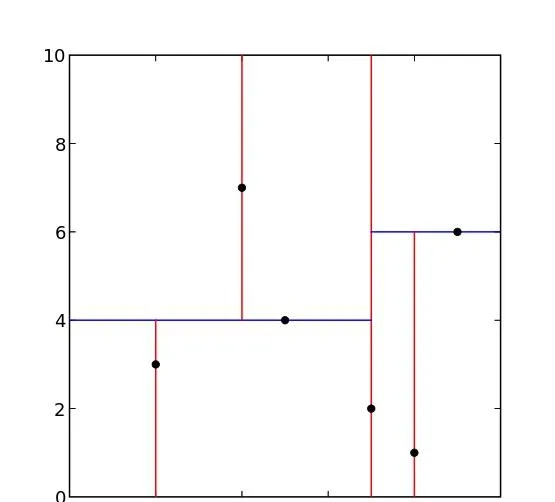
上述构造过程种最需要注意的是如何对数据进行切分，要平均划分就需要找到当前维度的中间值，有3种获取中间的方法。

根据堆排序或者归并排序对数组进行排序，时间复杂度 O(nlog^2n)
通过中位数算法 ^[1] 找到中间值，时间复杂度 O(n*logn)
实现对k维的数据进行排序并且保存，然后利用排序好的信息。时间复杂度 O(k*n*logn)

下面的示例代码是采用方法1构造K-d tree:

def get_k_median ( arr , axis ): arr . sort ( key = itemgetter ( axis )) return len ( arr ) // 2 def _construct ( self , points , depth ) -> Node : if not points : return None axis = depth % self . _k median = get_k_median ( points , axis ) node = Node ( points [ median ], axis ) node . left = self . _construct ( points [: median ], depth + 1 ) node . right = self . _construct ( points [ median + 1 :], depth + 1 ) return node

查找

k-d tree有以下2种查找方式：

最近邻搜索，查找距离给定点最近的k个节点。

范围搜索，查找距离给定点一定半径内所有的点。

查找最近的节点

查找最近的节点需要用到回溯算法，先找到叶子节点，计算2者之间的距离，由于叶子节点不一定是最近的节点，因此还需要判断是否相邻区域是否比当前叶子节点的距离更短。

def _query_nearest ( point , node , nearest , distance ): if not node : return if point [ node . axis ] <= node . value : _query_nearest ( point , node . left , nearest , distance ) else : _query_nearest ( point , node . right , nearest , distance ) if point [ node . axis ] <= node . value : if point [ node . axis ] + distance [ 0 ] > node . value : # check parent node t_distance = euclidean_distance ( node . element , point ) if t_distance < distance [ 0 ]: distance [ 0 ] = t_distance nearest [ 0 ] = node . element _query_nearest ( point , node . right , nearest , distance ) else : if point [ node . axis ] - distance [ 0 ] < node . value : # check parent node t_distance = euclidean_distance ( node . element , point ) if t_distance < distance [ 0 ]: distance [ 0 ] = t_distance nearest [ 0 ] = node . element _query_nearest ( point , node . left , nearest , distance )

查找半径内的节点

和查找最近的节点类型，只要把距离改成固定的值，如果查找的节点和给定点的距离在半径范围内，则添加，反之亦然，最后得到在指定点半径范围内的所有点。

def _query_radius ( point , node , plist , radius ): if not node : return if point [ node . axis ] <= node . value : _query_radius ( point , node . left , plist , radius ) else : _query_radius ( point , node . right , plist , radius ) if point [ node . axis ] <= node . value : if point [ node . axis ] + radius >= node . value : t_distance = euclidean_distance ( node . element , point ) if t_distance <= radius : plist . append ( node . element ) _query_radius ( point , node . right , plist , radius ) else : if point [ node . axis ] - radius <= node . value : t_distance = euclidean_distance ( node . element , point ) if t_distance <= radius : plist . append ( node . element ) _query_radius ( point , node . left , plist , radius )

总结

上述只考虑了构造和查找的过程，还没有包括添加、删除和再平衡的方法。当然有一些极端情况也需要补充，例如节点中某一维度有相等值的情况。

kd-tree的完整代码实现

参考

^https://en.wikipedia.org/wiki/Median_of_medians