这里用尽量浅显的语言来表达这样一个结论:
热力学中的吉布斯熵就是信息熵在热力学系统中的特定应用: 它是我们在已知某个热力学系统宏观状态的前提下,对系统微观信息的无知量 。
我们可以先从信息熵说起。
信息熵
举个例子,比如说你在考试的时候,遇到一道判断题,一道单选题,还有一道多选题。这三道题你都完全不会。这时候,你有机会偷窥其中一道题的答案,那么,你会选择偷窥哪一道题呢?
这是一个非常简单的选择,我们会选择多选题。但是为啥呢?
因为多选题最「难猜」。
一道判断题有两个可能答案,正确或错误。因此我们猜一个答案就有50%的概率可以蒙对。而一道单选题则有A、B、C、D四种可能答案,那么我们猜一个就有25%的概率蒙对。那么一道多选题呢,他有如下种可能答案:
A、B、C、D、AB、AC、AD、BC、BD、CD、ABC、ABD、BCD、ACD、ABCD
一个好的出题者会尽量让自己的题目达到最难猜的程度,也就是说,上述所有可能答案的概率都一样。也就是说,我们猜一个答案就只有1/15的概率蒙对。
也就是说,如果有人告诉我们答案,我们获得的信息量肯定是多选题>单选题>判断题。
这个例子告诉我们, 我们对一个问题的无知程度,取决于这个问题中可能选项的概率 。如果每个选项的概率都很低,那么我们就很难猜对答案,我们就对这个问题很无知。如果其中某一个选项的概率非常高,那么我们就有很大的自信去选择这个选项。于我们就对这个问题有相当的确定性。
消除我们更多的无知,就需要更多的信息;反之,如果只是消除一点点无知,则只需要一点点信息。于是这种信息量就是:
I\sim -f\left( p_i \right)
此外,如果我们有两个问题。告诉我们第一个问题的答案,我们就获得了 I_1 的信息量,告诉我们第二个问题的答案,我们就获得了 I_2 的信息量。那么把两个问题的答案全告诉我们,显然我们就获得了 I_1+I_2 的信息量。但是,从概率的角度,两个问题的正确概率却是每个问题的概率的乘积,也就是说:
I=-f\left( p_1p_2 \right)=I_1+I_2=-f\left( p_1 \right)-f\left( p_2 \right)
上述公式成立,就要求 f 是一个对数类型的函数。也就是说,信息量是由概率的对数来描述的。
对于一个特定的问题,它有若干种可能,每一种可能都对应着一个概率。那么,它的答案的信息量我们就可以取 所有这些可能选项的概率的对数的期望值 ,也就是:
S_S=-\sum_{i}{p_i\lg p_i}
这个就是信息熵。下标s这里表示是香农熵,以和后面的吉布斯熵做区分。
我们回到上面的例子,对一个判断题来说,有两种可能性,那么很容易算出来,其信息熵就是1比特。这很容易理解,因为我们只用0和1两个数字来编码对和错,就可以告诉我们答案了。对一个单选题来说,就是两个比特。也就是说,我们用这样的编码,00:A、01:B、10:C、11:D,就可以告诉我们答案了。而多选题,就是3.9个比特。因为我们用4个比特可以编码16种选择,但是这里只有15种选择,也就是说4比特略有冗余。
那么,信息熵和热力学熵又有何关联呢?
吉布斯熵
我们来看一个热力学系统。对这个系统的状态,我们应该如何描述呢?我们有两种方法。
第一种就是从微观角度来精确描述系统中的每一个分子的状态:这些分子的动量和位置。如果每一个分子的状态都被描述清楚了,那么整个系统的状态也就描述清楚了。这叫做 微观态(microstate) 。典型的热力学系统中大约有1mol的分子,每个分子有6个状态量:三个方向上的位置坐标和三个方向上的动量。那么典型的热力学系统的微观自由度就有 6\times 6\times10^{23} 个。也就是说,如果我们精确知道了这么多变量的数值,我们就得到了系统的全部信息。
在现实中,我们显然不可能知道系统的微观状态:这需要太多变量了。比如说,我们用一个单精度浮点数(32比特)来记录其中每一个变量,这种精度已经是很低的了。那么1mol最简单的单分子理想气体(比如说氦气),就需要我们用10YB的存储空间。据统计,2021年全球的总存储量大约是470EB。 [2] 也就是说,这个信息量是现在全球总存储能力的3万倍。
所以,在实际上,我们用第二种方法来描述热力学系统,就是从宏观角度。用几个变量来描述系统的整体,只看它在宏观上的表现,诸如温度、压力、密度、组成等等。这样一来,我们就忽略了它的每一个分子的具体运动状态。这种描述下的系统状态就叫做 宏观态(macrostate) 。一般而言,对一个系统,宏观态的自由度只有几个。这个自由度可以通过吉布斯相律来计算:
F=C-P+2
其中,C是系统的组分数,P是系统中包含的相态数。对于单组份单相系统(比如说一箱氦气),它的自由度就只有两个。大家常用温度和压力来描述这个状态(当然,也可以用诸如能量、熵、焓、自由能等状态函数)。
也就是说,热力学上, 我们对系统的描述就忽略了大量的微观信息 。
现在我们来问,已知一个宏观态,我们想要知道它的精确微观状态,我们需要多少信息量呢?
我们说,对已知的宏观态,有无数种可能的微观态。我们把这些可能的微观态出现的概率记作 p_i 。那么它的信息熵就是:
S_S=-\sum_{i}{p_i\lg p_i}
这就是吉布斯熵。事实上,吉布斯熵和信息熵在表述形式上有一点不同,科学家喜欢自然对数,而计算科学家们喜欢以2为底的对数。然后在补上一个玻尔兹曼常数:
S_G=-k_B\sum_{i}{p_i\ln p_i}
这就是 吉布斯熵 。(这里我们考虑离散情况,对于连续的情况,就把上述公式里的概率变成概率密度,把加和变成一个积分)
我们可以这么来看待吉布斯熵: 我们用简单的宏观自由度描述大量微观自由度的时候,所损失掉的信息量再乘以一个系数。
我们再来看看熵增原理。
熵增和混沌
从上面的讨论我们可以知道, 当所有的各种可能性出现的概率都相等的时候,我们对一个问题的无知度最高。 这一点很容易理解,当你面对一个选择题的时候,如果你知道B选项的概率高于其他选项,你对这道题的把握肯定会高于所有选项概率都相等的情况。
这恰恰就是平衡态。
也就是说, 平衡态有最大的熵,意味着平衡态是我们对系统最无知的一种状态。而系统总是向着熵增的方向演化,就意味着我们不断丢失系统的信息。
这一点我们可以进一步挖掘。
如果从系统的某个初态演化,如果我们通过微观动力学预测它未来的熵变,我们会发现整个过程中 熵守恒 ,而不是 熵增 。(这里说的是经典动力学,量子力学其实本质上和这个区别并不大,但这是另外一个故事了。)
也就是说,如果我们严格遵守底层规律,我们从初态知道多少信息,在未来就总会是无损的。这个其实很自然:因为从微观动力学看,一个保守系统其实是信息守恒的(动力学是完全决定论的,也即是如果知道一个初态,我们会准确预测它的未来)。
但是,这个看起来就和热力学第二定律出现矛盾了。问题出在哪里呢?
历史上,玻尔兹曼的一个统计力学基本假设就是 分子混沌假说(Stosszahlansatz) 。这个假说说的是,分子碰撞的速度之间是不相关联的。这显然是违背基本动力学原理的,因为它们都是来自动力学方程,显然不可能做到不相关联。在那个时候,混沌理论尚未建立。但是恰恰是这个未来才出现的混沌理论,为这个矛盾提供了一种解释。
混沌理论预言了两个关键动力学特征: 一个是演化对初始条件极端敏感;另一个是相空间的分形结构。 第一个特征意味着,相空间种的相体积会被不断拉伸,第二个特征意味着,演化过程中初始的相体积会变成任意精细的结构。这里我用一个简单的分形系统做一个直观的演示。
如下图,我们用一个简单的二维空间来表示一个热力学系统全部的可能微观状态空间(相空间)。某一个热力学系统在初始时刻从某个初始状态出发开始演化。我们对初始状态做出一个观察,由于观察精度所限,我们不可能得到一个精确状态,而只能得到一个可能的范围:蓝色的区域就是这个系统在初始时刻的可能初始状态范围(系综)。
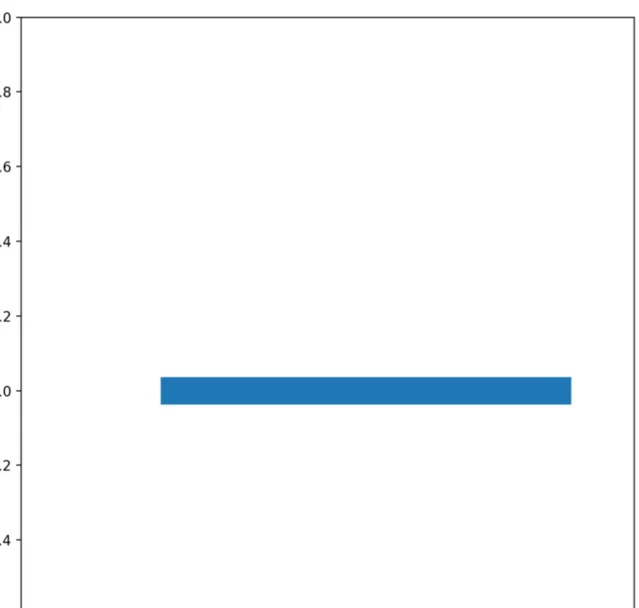
随着系统演化,我们通过动力学方程计算这个区域的状态随时间的变化情况。它会在状态空间中发生形变。前面说了,这个范围会不断拉伸(初始条件敏感)。同时由于系统的非线性特征,它还会发生弯折、扭曲等一系列形变。由于信息的守恒,这个 范围所覆盖的面积却不会发生变化 。下面就是一种非常简单的演化方式:它只涉及了拉伸和弯曲两种形变,这个形变过程就形成了一种叫做 「龙之曲线」 的分形结构(视频用python写成)。
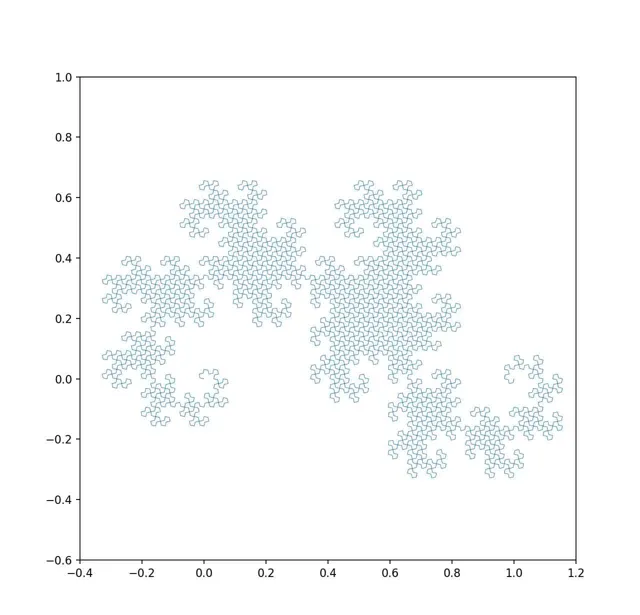 「龙之曲线」的演化历史
https://www.zhihu.com/video/1449765365841006592
「龙之曲线」的演化历史
https://www.zhihu.com/video/1449765365841006592
我们可以看到,系统从一个初始的小范围可能性(小面积)最终变成了一个大范围可能性(大面积)的过程。
但是,我们的演化规则却是,这个范围所覆盖的面积不发生变化。这里的关键就在于,随着演化的过程,初始的面积被越拉越长,变成了一条细线。随着不断拉伸,这条线越来越细。但是我们的观察精度却不允许我们 识别 无线精细的线形,所以到了一定程度后,我们所观察的线形就不再继续变细了 - 虽然「实际上」它在变细,但是我们却无法观察了。最终,这个范围的演化越来越精细,看上去就成了一个范围更大的面积。这个,吉布斯把它叫做「 粗粒化 」。也就是说,在相空间中,我们无法识别足够精细的结构,而只能把这个相空间分成有限体积的「像素」看待。通过这种变化, 我们就在一定的精度之外,丢失了系统的进一步演化信息。
这种分形结构,是混沌理论的一个预言。关于分形,这里就不多说了,请参考
的确,如果我们可以不断提高我们的观察精度,我们的确可以看到足够精细的结构,从而「还原」出它的细线本质(视频由python写成):
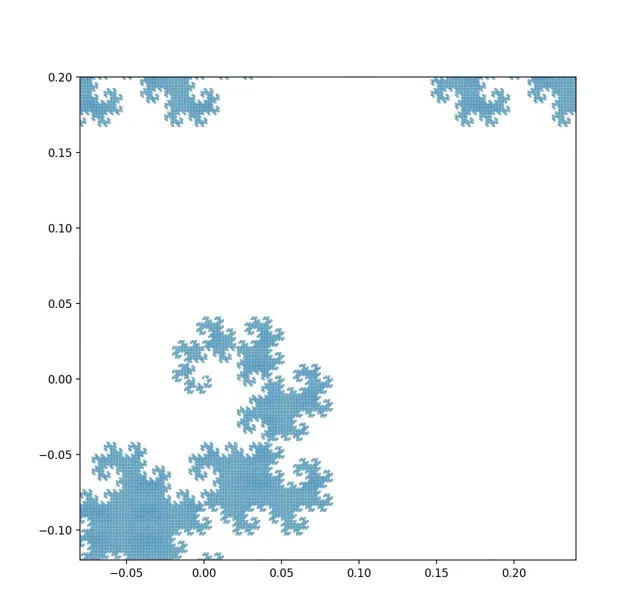 揭示龙之曲线的精细结构
https://www.zhihu.com/video/1449768887402942464
揭示龙之曲线的精细结构
https://www.zhihu.com/video/1449768887402942464
但是,统计力学本身就是一个粗粒化的学科。如果我们不需要粗粒化,也就不需要统计力学了。
当然,这种粗粒化的解释、吉布斯熵和玻尔兹曼熵以及热力学熵(克劳修斯熵)之间的关系、乃至系综方法本身,现在也都存在着诸多的争议。这就是另外的故事了,本文不涉及。我计划在未来为我的专栏里写的文章里加以覆盖。这是一个已经停更两年的专栏了,最近计划拾起来继续更新,这里先做一个广告:
前面我们从统计力学的角度,大概讲了一下系统演化过程中的信息丢失过程,进而把熵增归结于信息的丢失。那么从热力学的角度,我们如何把信息和熵联系在一起呢?
信息熵和热力学熵
我们可以这么来说,从热力学角度, 一个系统的熵表征着它内部「废能量」的多少 。所谓的「废能量」指的是在现有的热力学条件下无法用来对外做功的能量。
也就是说,熵越大,系统对外做功的能力越小。熵越小,系统对外做功的能力越大。如果联系到我们上面所说的信息熵和热力学熵的关系,这句话可以直观地理解为: 我们对系统了解越多,则我们可能利用系统对外做的功就越多。
这句话其实挺好理解,也挺容易想象的。
比如说,我们有一个水库,水库看起来很平静。如果我们比较粗糙地观察它,我们认为它处在平衡态,是一个熵最大的状态,因此我们无法用它来做功。
但是如果我们在水库中放置多个传感器,我们就会发现在表面的平静状态下,它内部其实暗流涌动。很显然,从热力学可以计算,有暗流的水体有着比平衡态的水体更低的熵:这和我们前面的论述相一致,因为我们对水体的监控更加细致,也就有着更多关于水体的信息了。
假如说我们手中有一个引擎,并且通过某种操作可以把它放置在水中任意一个地方。于是我们就可以通过我们对暗流的监控,随时把这个引擎放在暗流最大的地方。通过这种暗流就可以推动引擎做功。也就是说,这时候我们发现水库就有了对外做功的能力了。
我们对水库的监控越精细,我们对它的信息就了解得越多,因而我们对水体所观察的熵值就越低,而此时我们操控引擎做功的能力就越大。
聪明如你,你应该立刻意识到,这个引擎的操作员其实就是一个粗糙版的麦克斯韦妖。只不过我们把麦妖放在了一个相对宏观的情形下了。
问题是,我们本身都是宏观的物体,因此我们在这种有宏观效应的涨落中,就可以通过获取更多的信息来做功。在微观世界里,情况就很复杂,比如说著名的Szilard引擎。 [3] 这里涉及到一个信息的处理和读写的极限的问题。也就是著名的 「麦妖驱魔」(Exorcism of Maxwell Demon) 问题。 [4] 当然,这就是另外一个故事了。
参考
- ^ doi.org/10.1119/1.1971557
- ^https://www.statista.com/statistics/638593/worldwide-data-center-storage-capacity-cloud-vs-traditional/
- ^https://en.wikipedia.org/wiki/Entropy_in_thermodynamics_and_information_theory#Szilard's_engine
- ^https://en.wikipedia.org/wiki/Maxwell's_demon











