民科好多啊…… 可惜专搞 GR(广义相对论)的几个大牛都没出现,只好让我这个半民科顶上去了。
John Wheeler (费曼的老板,「黑洞」概念的提出者)有句话,请记住它:「质量告诉时空如何弯曲,时空告诉质量如何运动。」
再记住这句话:质点在弯曲时空中运动时,轨迹会受到时空弯曲的影响,就跟受到一个力一样;人们为了方便,管这个表现叫「引力」。
够了,剩下的就是数学了。当然,要是有人愿意用民科式的脑补来填充,咱也没辙啊。
说出「黑洞附近因为巨大的引力产生了空间扭曲」的人,放学别走。写给外行看,也得保证措辞尽量严谨啊。科普也要按照基本法,识得唔识得噶?
最后,澄清两个概念。
首先,弯曲的东西,是时空,而不仅仅是空间。在老爱之前许多年,黎曼本人就试图用空间弯曲解释引力:因为,自伽利略指出「引力质量 == 惯性质量」(你可以通俗地将这个等号理解为「从比萨斜塔上往下扔一大一小俩球结果这俩同时落地」,虽然伽利略其实并没有做过这事儿)以来,人们发现,这一事实在牛顿力学的框架下实在是太不自然了(两个不相关的物理量竟然完全相等),几乎唯一的「看上去自然」的解释就是「引力是几何效应」(这使得这两个物理量事实上成了一个东西)。可惜因为当时完全不可能对「时空」有什么认识,黎曼没有把时间维度放进去,所以碰了一鼻子灰(对 GR 微扰有经验的人应该能立即想到,在弱场下,跟牛顿引力势长得差不多的那个东西,正是出现在与时间有关的分量上)。
其次,在一般情形下,我们一般不会使用「扭曲」这个字眼。「扭曲」在 GR 里有着特殊的内涵:不为零的挠率,也就是适应度规的联络张量 \Gamma^{a}_{\ b c} 的两个下指标 b 和 c 不能交换。而通常说的「时空弯曲」,指的是时空的黎曼曲率张量不为零。有挠率的 GR 被研究得不多,部分地因为老爱在最早版本的 GR 中就假定了挠率为零而被大家因袭,也部分地因为有挠的 GR 在很多方面与观测不符(比如,最简单地,挠率的源是什么?你觉得粒子自旋好使么?)。现在有人试图用宇宙尺度上的挠率替代暗物质,也把那张 Hubble diagram 拟合上了(当然,关于 Hubble diagram 的许多拟合都有 overfitting 之嫌,这项工作也不例外);不过,提出这个模型的人自己都说「姑妄言之姑听之」了,大家便也没有太认真地对待。
通俗地说,「弯曲」指的是这样的情形:把一个矢量从 Q 平移到 P,有「上路」和「下路」两种走法(看下图中的那个「平行四边形」),而通过两种走法平移过去的矢量 [ 下图中的 v_a(P) 和 \tau_a(P) ] 是不能重合的——这意味着,你好端端地试图朝前走,时空的弯曲却偏要来搡你一把,这「搡你一把」就是引力。

(图片来自
http:// arxiv.org/abs/0804.3742,这是我见过的废图和废话最多的物理学博士论文之一)
而若时空是「扭曲」的,则上图中的那个「平行四边形」根本不能存在,得缺个口儿:
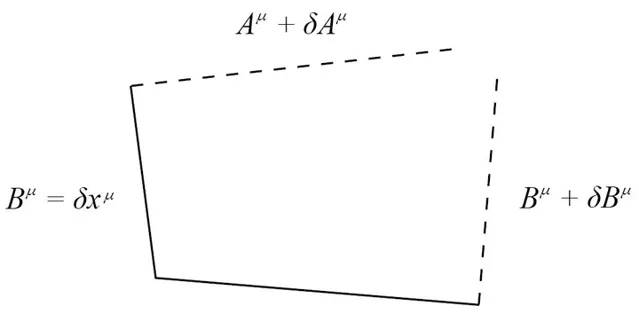
(图片来自:
http:// arxiv.org/abs/0903.2565)











