这次谈Spatical Computing(长文)
也算是【从GPU谈异构(14)】吧
(♧◑ω◑)☞♡☜(◐ω◐♧) 随性随性
Spatial翻译成中文,妥妥滴高大上
空间计算,当然以此对应是时间计算。
中二的你是不是立刻想打一个响指。
其实也没错了,你想到了他。

还有他……

没错,他是卷福、是福尔摩斯、是奇异博士、是图灵
这只是他在不同时空中不同的分身
ԅ(¯ㅂ¯ԅ)ԅ(¯ㅂ¯ԅ)ԅ(¯ㅂ¯ԅ)
抖机灵结束,这是因为所有话题都脱不开下面这个起点,图灵机和图灵可计算。
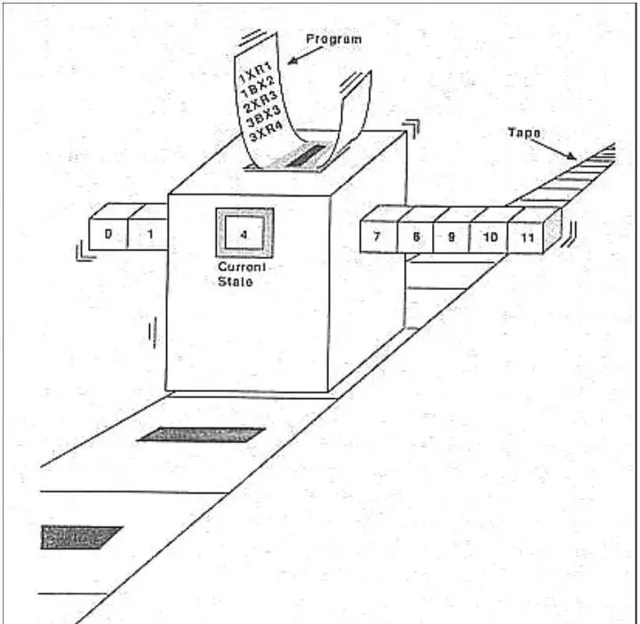
奇异博士手上的是时间宝石,能够掌控时间。
但必须要澄清的是,在另一个电影里,图灵手上的其实是空间宝石。
包括很多EE甚至CS的同学都没有明白图灵和丘奇到底做了什么。
他们的核心力量其实是在虚无中标定了一个空间,那是 无尽问题空间 中的 数学问题空间 中的 可判定问题空间 中的 有答案问题空间 中的 可计算空间!
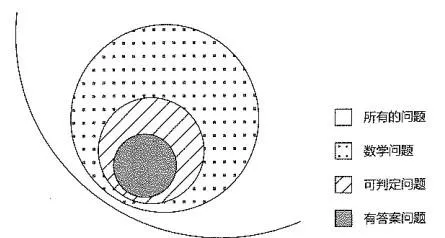
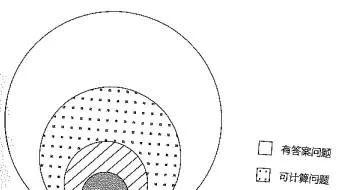
那就像是在无尽的宇宙中寻找到了地球,一个适宜CS+EE 工程师快乐成长、努力奋斗、脱发明志的天堂。
图灵可计算的原理不在本文范畴,这里想澄清的是,图灵之后,人类有了一个判定基准,即先衡量一个问题是否属于图灵可计算,如果是,就可以从裤裆里掏出图灵机,盘它。
举个反例,ising问题就是来自有答案空间但非图灵可计算空间的邪恶的古尔丹。
不过,图灵可计算只是化开了天地,肉体凡胎的程序猿又如何能上天入地呢?
这个剧本里,真正手握时间宝石的是冯诺依曼。他长的没我帅就不放图了。
冯诺依曼创造了冯诺依曼架构,而在该架构运行的图灵可计算,我们可以把它称为temporal computing,即时间计算。
与此对应,我们通常把图灵可计算中的非冯诺依曼架构上运行的图灵可计算称作spatial computing,即空间计算。
可能很多同学对这个冯和非冯的时空定义很不解,教科书不是这么说的对吧。
我举一个栗子方便理解,再下面就好说了。
我们可以把一个图灵可计算问题类比为我从宇宙中心五道口出发,要到达天安门广场看升旗的问题。
很多同学会说,咯,你打开地图,从这里到这里不就好了?
话是这么说没错啦,这就是图灵和丘奇都是数学家,而冯诺依曼是工程师的差别。你得用工程师的思维来考虑这事。
你先到哪儿? 再到哪儿? 用什么交通工具? 要不要吃个饭? 有没有遇到熟人? 会不会迷路?
一个真正的工程师,会考虑到所有可能的变化并给出完备的应对,最终达成mission completed。
冯诺依曼给出的答案就是折叠时间,它创立了内存和堆栈的概念,在发生任何事情的时候冯诺依曼架构都能够将当前 时间状态冻(保)结(存) ,以上面的题目为例,就像地图折叠起来,一段一段路,都变成了独立的行为片段(固定存档)。
如果无事发生,那就逐段进行即可,但如果发生任何事件,都能够时间回(读)退读(档),重新出发。你可以重温一下奇异博士的剧情,就是他打败多玛姆的剧情,是的,这就是冯诺依曼架构(你可以试图把主角的面孔换成冯诺依曼)。在冯诺依曼架构下,你也可以的,甚至更进一步,来一个多线程的任务(多时空),你一边在从五道口去天安门,一边又在从陆家嘴出发去松江加班,你都可以基于时间片化身无数,单人刷完全部副本。
这就是时间计算!
这也是一个数学家和一个工程师最大的区别
数学家的直肠子想的是如何快速解决一个问题
而工程师考虑的是如何建立可以一个长期稳定的解决问题的方法,因此才诞生了冯诺依曼架构并且成为解决图灵可计算问题最主流的硬件框架。
那么,从工程师认可的长期稳定的解题路径- 时间计算(冯) ,到让工程师觉得还不那么靠谱的 空间计算(非冯) 变得靠谱。中间需要解决什么问题,才能获得一个可用或者至少专用的空间计算(非冯)机器? 肯定不是简单地把整个计算图平铺打开,让每一个人都快乐且高效地到达终点那么简单,要这么简单,冯诺依曼就是个瞎子啊。
在我的认知中,spatial computing要跨过三重大山,每重山上要过三座崖,才能算得上可用,否则永远都只能在数学家的梦里。
第一重山是最难的,那是:变化(divergence)spatial computing需要首先解决各种计算的变化问题。要过这重山得过三座崖,一座更比一座艰难,那分别是: 分支、递归、异常。
分支, 其实是最容易解决的,不就是做多选题嘛,大不了我把所有分支条件都模拟出来,也就是我把整个北京地图全展开,你从五道口去天安门不是? 就算你去大兴机场绕一圈,我也给你把计算图布上了,而且就算你不去大兴,别人总会去嘛,资源也没白费。
注:AI的MoE就是典型的分支执行,大家训练的时候其实就全部署上了(也有人叫他稀疏)。
递归, 是相对麻烦的事情,我看我家儿子就是这样,好好走着走着,突然看到个啥,就凑过去死循环了……这里的不确定性很大,没有特别好的办法。要解决,首先需要保持图灵完备,这也是RISC-V在空间计算中用作PE的主要原因,其次,内存管理要下沉,不能在编译器做,得到PE做,再次,祈祷呗,祈祷算法相对没那么恶心,当然要真实在不行,那就偶尔来个万爷等一孙也就忍忍算了,毕竟回忆一下,多人出游的时候,总有一个二逼迟到不是。
注:AI的动态tensor就是典型的递归 但是AI的算法都是成熟的调参侠写的,相对没那么深,大多数情况都在控制范围内。
异常 ,才是所以这个山最难跨越的关卡。难在什么地方呢? 难在科学家不理解……
工程师和科学家经常的吵架就是:「这里的RAS很难处理的」,「RAS对解决问题没有收益」,「系统这么大,出错的概率是累进的」,「我们先解决问题,再来考虑RAS」…………
这个世界的工具,从来就没有绝对可靠可言,都是概率,要算的。我曾经有一个帖子,有些潜在的问题,已经在逐渐变得明显了。已经到了数学家你不能不考虑程度了。
异常是什么呢? 还是以从五道口去天安门为例,你开车出门,想着顺道去鼓楼大街看看新出的游戏,小小分个支,没毛病。买了新游戏一开心你想着顺便在锣鼓巷吃点小吃,递归了不是,也没多大个事。关键是你顺手喝了两杯酒,上车一启动碰上查酒驾的,哦豁,异常了,进局子了。
进局子了,这事在空间计算(非冯)架构里,没法处理,因为整个计算状态走到哪儿算哪儿,没存档,得整个重来。要仅仅是五道口到天安门还好,怕的是这其实是整个人生中的一天,那完犊子了,可能整个人生就灰暗了啊,你玩的是一命到底的地狱模式。
算法的下一步演进,必须要逐渐考虑到对硬件的容错性,数学家必须要能够理解现实的残酷,把RAS融入图灵可计算空间的本身(缩小空间)。
注:我乐观地期待AI的算法能够最快地找到这个答案,例如多路径(MoE多专家激活)
题外话:冯诺依曼怎么处理前面的进局子问题呢? 存档啊,状态写入内存呗,干干净净进局子就当在另一个世界穿越体验一下生活呗,玩完了你读个档啊,状态回到你进锣鼓巷的时候,该吃吃该喝喝还能重新享受一下,因为你读过书,你知道同样的招数对圣斗士是没用的,你再上车,一启动,又碰到警察! 又进局子了,原来警察也读档了…………终于你在局子里进进出出几次之后,你明白了,冯诺依曼不是圣斗士,你得在读档之前搞定警察才能最终到达天安门…………
 第二重山是我跨不过的,那叫做图编译
第二重山是我跨不过的,那叫做图编译
spatial computing需要能够对应用进行图编译,即编译成图而不是简单的指令流。我确实没学过编译器,大致上只能用芯片设计的综合工具来类比其语言翻译和优化的流程
如何才能把一个图灵可计算问题分解为计算,请教过很多人,有人跟我讲很简单,都能做,也有人说特别难,综合各种信息大致推理:编译器本身学的人不多,而编译器本身却囊括了非常巨大的知识空间,其内部有非常多的技术分支,图编译及布局更属于其中的偏门,即使菊厂号称全中国编译器能力第一,也并没有囊括图编译及布局方面的人才。而从业界的情况来看,空间计算在美国也能有好几家startup在做(cerebras、tenstorrent、tesla等等),但看中国大陆一家类似的startup公司都没有,大致上,编译器的人力配比也是如此这般吧。
这事我不是行家,也希望业界有人能指点一下。
第三重山,是互联和通信spatial computing相比冯机需要更加强大的片上片间的互联通信能力。
空间计算(非冯)和时间计算(冯)最大的不同,就在于数据流方向。
冯诺依曼架构的核心是增加了内存,所以信息交互、状态保存,都是基于内存为中心进行的,也就是所有的PE访问内存就罢了,而内存具有无依赖特征,也就是除非疯狂玩锁,PE之间的依赖关系都可以通过内存消除。
但非冯架构完全不一样了,他没有全局的shared memory,数据在PE直接传递,所以数据流的核心是解决PE之间的交互和依赖。嗯很多人简单理解空间计算就是控制好PE之间互相读写就好,实际上,PE之间的依赖解除,防止wormhole死锁才是关键(编译器全预分配内存也能解死锁,但我觉得那样编译器负担和约束太大)。
我还没有完整地跑过一颗大号的空间计算芯片,所以这重山我并不能说迈过了。但我是做互联技术出身的,在业界玩互联怎么说也算是第一阵营,这山再高,热热身向上冲就是了。
我们也可以看看业界怎么解决这个问题的
(๑> <๑)
graphcore是个很有趣的例子,它使用了BSP编程模型,这里不深度解释BSP的原理,简单来讲就是它把计算和通信分割成独立phase,这样依赖关系就被完全打破了,写算法也变得简单,顺着节拍,来,药药药,切克闹……
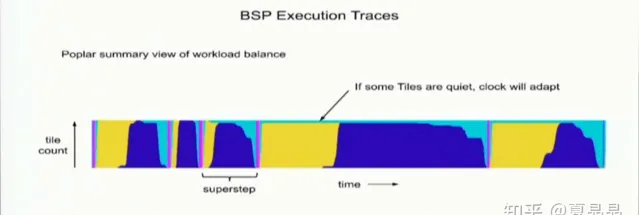
BSP计算模型的创始人Bill McColl也就在菊花厂任职,聊过,数学家,对这个算法很自豪。但是作为一个工程师,我对他是无语凝噎。
这种计算模式,数学家是舒服了,工程师都在吐血。
这种全局同步启动和停止的方式,这负载变化引发的巨大的电流变化最终一定会触发电压无法稳定,这对系统的电源完整性是极大的挑战! 大家都知道关灯一小时活动吧? 极其反智,幸好跟着玩的人还不多,等什么时候欧洲的白左们都信了,把工业电也跟着一起玩,我就坐看欧洲发电、变电站放烟花了。
graphcore也是如此,这颗芯片我估计其启停之间的高频电源噪声得有100mV,除非定制电源模块(响应时间小于5us?),并且编译器控制好启停的mininal period,并且在exchange phase有意拉高Vdd以备PE启动的IR drop,否则根本玩不转,而即使玩转了,能耗表现也是有破绽的。
相反tenstorrent则采用了另一个剑走偏锋的技术路径。我曾经形容,groq的芯片是把整SOC大芯片做成了一个单核CPU,而tenstorrent则是把他的SOC大芯片做成了内含120个小SOC的松散联盟(wormhole为例),它的每个核,其实都是cpu+mem+NIC的完整体,编程上,采用了actor模型,我觉得这是一条正确的道路。按照自媒体的风格,喊出:jim keller一级棒,就好了。

要做一个可用的spatial computing,我讲了有这么多困难,这么多重山要跨越,那么问题来了。
为什么我们要做spatial computing呢?
价值是什么? 继续用冯诺依曼架构它不香吗?
OK,让我们还是回到patterson教授讲述DSA时候的胶片,想一想他神秘的微笑。
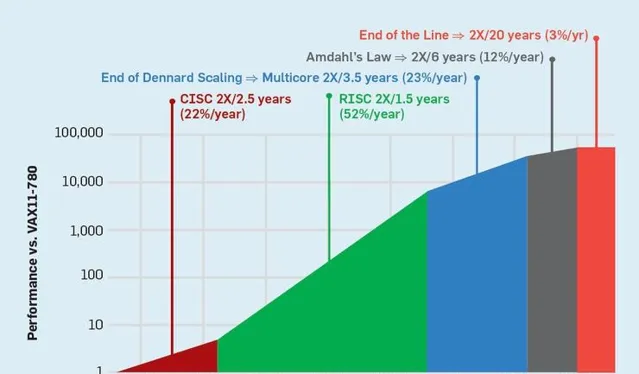

一、spatial computing是一种DSA,因为它没法像冯诺依曼架构那样的普适性,它大概率也只能解决一部分的问题,但效率会更高。
二、AI即神经网络的形态,更接近于计算图的形态,只要数学家们真正认识到硬件容错性的重要性,在算法中支持了容错,MoE、动态shape反而都是能够客服的问题。
三、也是最重要的一点,冯诺依曼架构性能提升的黑色地带Amdal's Law还有肉眼可见将来的memory wall。spatial computing是可见的能够突破Amdal's Law和memory wall,持续扩展算力的唯一路径。在空间计算的范畴下,问题的复杂度也不再依赖于摩尔定律,仅仅依赖于系统规模是否与问题规模匹配,也就是这只是一个充钱的问题

极端脑洞下,你甚至可以制造一个spatial computing的戴森球计算机。
有同学对我的观点有些误解,总结一下。
我是支持并希望去挑战spatial computing的,虽然我前面讲了那么多困难,异常、图编译器,都是计算机体系结构中世界级的难题。但不能因为他们难就退缩啊,因为这些题目难,还没有难到无解,而amdal law和memory wall那是让人绝望的困难。
只要你跨越前面提到的这重重山,你所能得到的,那是无尽的宝藏。











