来来来,题主,就按照你的思路,咱们来算一下呗!
首先,为了便于理解,我们挑一个最简单的图形,就比如 \[y = {x^2}\] 吧。
我们来试着计算一下该函数在区间 \[\left[ {0,1} \right]\] 上的图像与 x 轴所围成的面积,即下图阴影部分面积:
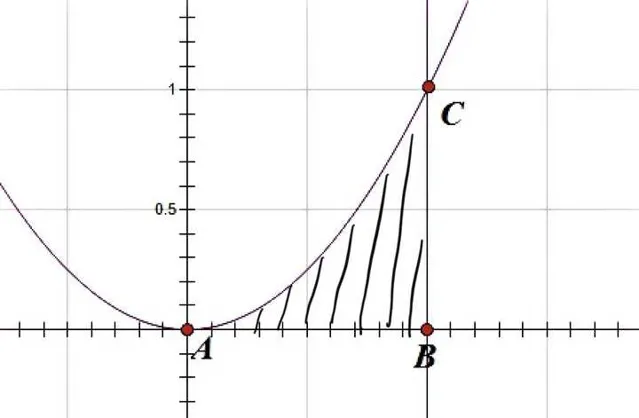
为了方便起见,就假设它的面积等于 S 吧,咱们接下来就是想办法把 S 的具体数值给算出来。
好,接下来咱们就用题主说的细矩形来逼近,第一次我们将区间\[\left[ {0,1} \right]\] 分割成两部分,分别是 \[\left[ {0,\frac{1}{2}} \right]\] 与 \[\left[ {\frac{1}{2},1} \right]\] 。
那如何确定矩形呢?我们采用的分割方法是,以 区间内二次函数的最小值为矩形的高 。
在区间\[\left[ {0,\frac{1}{2}} \right]\] 内,\[y = {x^2}\] 的最小值在 \[x = 0\] 处取得,此时 y=0 ,故此时矩形的高为 0 。
在区间\[\left[ {\frac{1}{2},1} \right]\] 内,\[y = {x^2}\] 的最小值在 \[x = {\frac{1}{2}}\] 处取得,此时 \[y={\left( {\frac{1}{2}} \right)^2}\] ,故此时矩形的高为 \[{\left( {\frac{1}{2}} \right)^2}\] 。
如下图所示,不过因为第一个矩形的高为 0 ,所以在图上无法看出,但读者在心里应该看到下图有两个矩形:

这两个矩形的面积之和为多少呢?
我们用 \[{a_2}\] 表示这两个矩形的面积之和,那应该有:
\[{a_2}\]
\[ = \frac{1}{2} \times {0^2} + \frac{1}{2} \times {\left( {\frac{1}{2}} \right)^2}\]
\[ = \frac{1}{2}\left[ {{0^2} + {{\left( {\frac{1}{2}} \right)}^2}} \right]\]
\[ = \frac{1}{{{2^3}}}\left( {{0^2} + {1^2}} \right)\]
应该看到,因为这两个矩形都完全的在二次曲线的内部,即这两个矩形的面积必然是要小于 S 的,所以我们有: \[{a_2} \le S\] 。
接下来,我们继续分割,将区间\[\left[ {0,1} \right]\] 分割成三部分,即: \[\left[ {0,\frac{1}{3}} \right]\] , \[\left[ {\frac{1}{3},\frac{2}{3}} \right]\] , \[\left[ {\frac{2}{3},1} \right]\] 。
接着确定矩形,套路还是一样的,以 区间内二次函数的最小值为矩形的高 。
在区间\[\left[ {0,\frac{1}{3}} \right]\] 内,\[y = {x^2}\] 的最小值在 \[x = 0\] 处取得,此时 y=0 ,故此时矩形的高为 0 。
在区间\[\left[ {\frac{1}{3},\frac{2}{3}} \right]\] 内,此时矩形的高为 \[{\left( {\frac{1}{3}} \right)^2}\] 。
在区间\[\left[ {\frac{2}{3},1} \right]\] 内,矩形的高为 \[{\left( {\frac{2}{3}} \right)^2}\] 。
还是要注意,下图看上去只有两个矩形,但读者的心里应该明白有三个矩形,第一个矩形只是因为它的高为 0 所以无法画出,但并不意味着它不存在。
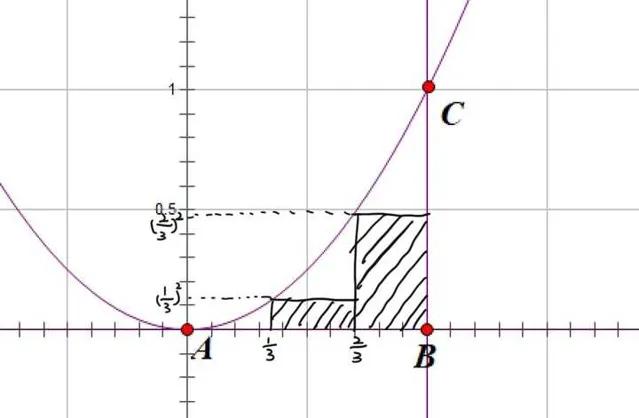
我们用 \[{a_3}\] 表示这三个矩形的面积之和,还是一样的:
\[{a_3}\]
\[ = \frac{1}{3} \times {0^2} + \frac{1}{3} \times {\left( {\frac{1}{3}} \right)^2} + \frac{1}{3} \times {\left( {\frac{2}{3}} \right)^2}\]
\[ = \frac{1}{{{3^3}}}\left( {{0^2} + {1^2} + {2^2}} \right)\]
且这三个矩形也是在二次曲线之下,故有: \[{a_3} \le S\] 。
最后我们再试试将区间\[\left[ {0,1} \right]\] 分割成四部分的形式,此时会有四个矩形:

则 \[{a_4} = \frac{1}{{{4^3}}}\left( {{0^2} + {1^2} + {2^2} + {3^2}} \right)\] ,且 \[{a_4} \le S\] 。
按照这种划分方法,我们很容易得到,当我们将区间 n 等分时, n 个矩形的面积之和为:
\[{a_n} = \frac{1}{{{n^3}}}\left( {{0^2} + {1^2} + \cdots + {(n-1)^2}} \right)\]
且 \[{a_n} \le S\] 。
我们再算一下当 \[{n \to +\infty }\] 时的情形,即
\[\mathop {\lim }\limits_{n \to \infty } {a_n} = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}}\left[ {{0^2} + {1^2} + \cdots + {{\left( {n - 1} \right)}^2}} \right]\]
我们有公式 \[{1^2} + {2^2} + \cdots + {n^2} = \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\]
将 n-1 代入,我们有: \[{1^2} + {2^2} + \cdots + {\left( {n - 1} \right)^2} = \frac{{\left( {n - 1} \right)n\left( {2n - 1} \right)}}{6}\]
故: \[\mathop {\lim }\limits_{n \to \infty } {a_n}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}}\left[ {{0^2} + {1^2} + \cdots + {{\left( {n - 1} \right)}^2}} \right]\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}} \cdot \frac{{\left( {n - 1} \right)n\left( {2n - 1} \right)}}{6}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot \frac{{\left( {n - 1} \right)n\left( {2n - 1} \right)}}{{{n^3}}}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot \frac{{n - 1}}{n} \cdot \frac{n}{n} \cdot \frac{{2n - 1}}{n}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot \left( {1 - \frac{1}{n}} \right) \cdot 1 \cdot \left( {2 - \frac{1}{n}} \right)\]
\[ = \frac{1}{3}\]
所以最后我们得到: \[\frac{1}{3} = \mathop {\lim }\limits_{n \to \infty } {a_n} \le S\]
题主的意思就是,既然每次划分的时候,矩形的面积之和一直小于 S ,那你凭什么认为最后 S 的面积就是 a_n 的极限?
别着急,接下来我们再看一种划分方法!
这次还是先将区间\[\left[ {0,1} \right]\] 分割成两部分,分别是 \[\left[ {0,\frac{1}{2}} \right]\] 与 \[\left[ {\frac{1}{2},1} \right]\] 。
但我们如何确定矩形呢?这次采用的分割方法是,以区间内二次函数的 最大值 为矩形的高。
在区间\[\left[ {0,\frac{1}{2}} \right]\] 内,\[y = {x^2}\] 的最大值在 \[x = {\frac{1}{2}}\] 处取得,此时 \[y={\left( {\frac{1}{2}} \right)^2}\] ,故此时矩形的高为 \[{\left( {\frac{1}{2}} \right)^2}\] 。
在区间\[\left[ {\frac{1}{2},1} \right]\] 内,\[y = {x^2}\] 的最大值在 \[x =1\] 处取得,此时 y=1^2 ,故此时矩形的高为 1^2 。
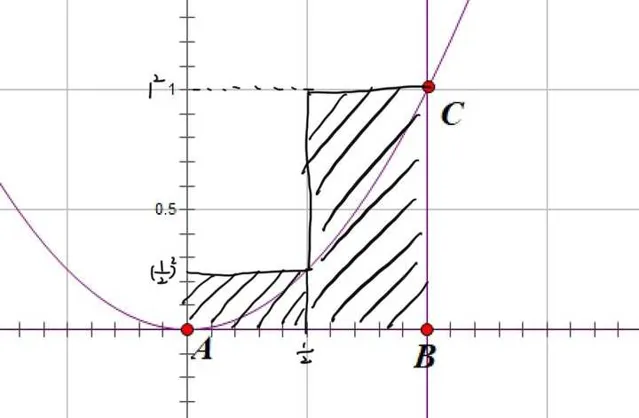
这两个矩形的面积之和为多少呢?
我们用 \[{b_2}\] 表示这两个矩形的面积之和,那应该有:
\[{b_2}\]
\[ = \frac{1}{2} \times {\left( {\frac{1}{2}} \right)^2} + \frac{1}{2} \times {1^2}\]
\[ = \frac{1}{2}\left[ { {{\left( {\frac{1}{2}} \right)}^2}} +{1^2} \right]\]
\[ = \frac{1}{{{2^3}}}\left( { {1^2}} +{2^2} \right)\]
应该看到,这次这两个矩形完完全全的覆盖了二次曲线,所以这两个矩形的面积必然是要大于 S 的,所以我们有: \[S \le {b_2}\] 。
我们继续分割,将区间\[\left[ {0,1} \right]\] 分割成三部分,即: \[\left[ {0,\frac{1}{3}} \right]\] , \[\left[ {\frac{1}{3},\frac{2}{3}} \right]\] , \[\left[ {\frac{2}{3},1} \right]\] 。
接着确定矩形,套路还是一样的,以区间内二次函数的 最大值 为矩形的高。
这三个区间矩形的高分别为: \[{\left( {\frac{1}{3}} \right)^2}\] , \[{\left( {\frac{2}{3}} \right)^2}\] , 1^2 。
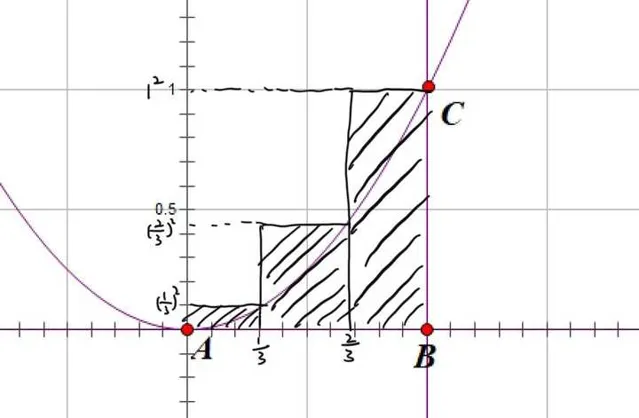
然后 \[{b_3}\]
\[ = \frac{1}{3} \times {\left( {\frac{1}{3}} \right)^2} + \frac{1}{3} \times {\left( {\frac{2}{3}} \right)^2} + \frac{1}{3} \times {1^2}\]
\[ = \frac{1}{{{3^3}}}\left( {{1^2} + {2^2} + {3^2}} \right)\]
且 \[S \le {b_3}\]
最后,我们依照下图,计算一下 b_4
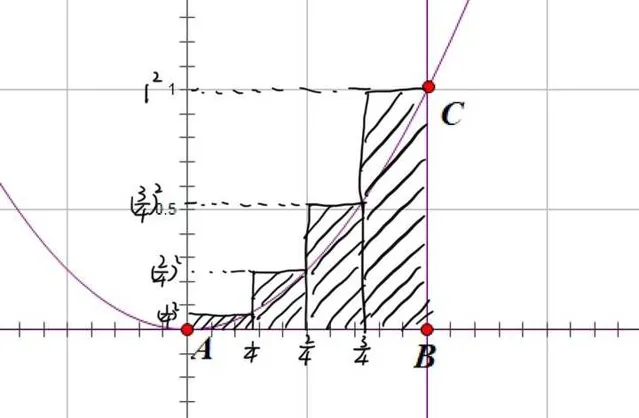
\[{b_4}\]
\[ = \frac{1}{4}\left[ {{{\left( {\frac{1}{4}} \right)}^2} + {{\left( {\frac{2}{4}} \right)}^2} + {{\left( {\frac{3}{4}} \right)}^2} + {1^2}} \right]\]
\[ = \frac{1}{{{4^3}}}\left( {{1^2} + {2^2} + {3^2} + {4^2}} \right)\]
最后,我们很容易的得到了这种划分方式的通项公式,即: \[{b_n} = \frac{1}{{{n^3}}}\left( {{1^2} + {2^2} + \cdots + {n^2}} \right)\]
又因为这种划分下,这些细矩形是可以覆盖掉整个二次曲线围成的图案的,故 \[S \le {b_n}\]
最后再计算一下 b_n 的极限,
即 \[\mathop {\lim }\limits_{n \to \infty } {b_n}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}}\left( {{1^2} + {2^2} + \cdots + {n^2}} \right)\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{{{n^3}}} \cdot \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{1}{6} \cdot 1 \cdot \left( {1 + \frac{1}{n}} \right) \cdot \left( {2 + \frac{1}{n}} \right)\]
\[ = \frac{1}{3}\]
而我们又有 \[S \le \mathop {\lim }\limits_{n \to \infty } {b_n} = \frac{1}{3}\]
而我们之前又有\[\frac{1}{3} = \mathop {\lim }\limits_{n \to \infty } {a_n} \le S\] ,通过夹逼定理,我们得到了 S 是真的等于 \[\frac{1}{3}\] ,换句话说,用细矩形面积的和逼近时,随着划分的越来越细,误差是趋近于 0 的。
好的问题会对数学的进步产生推动作用,题主无疑提了一个很好的问题,那顺着这个思路,我们有哪些思考方向呢?
首先是这篇回答我简单的说了一下两种划分方法,分别是取区间内函数的最大值与最小值作为矩形的高,最后发现当 \[{n \to +\infty }\] 时,就不存在误差了。
这件事其实暗含了极限理论的基本思想,极限到底是什么?是指两个数很近很近吗?
而如果将这种划分思路一般化,在数学里我们将其称为 达布上和 与 达布下和 。
自然的,在这个二次函数的例子里我们发现最终的结果是达布上和等于达布下和,事实上,有许多函数都满足这一性质,我们将这些函数称为黎曼可积的
那是否存在一些函数,它的达布上下和不相等呢?
有的,这种情况下我们将其称为黎曼不可积
最后,在这篇文章中,我们划分的是 x 轴,那请问有没有划分 y 轴的方法呢?
也是有的,我们将其称为勒贝格积分……
好吧,我们已经说的够远了,就此打住吧。











