前三部分引路:
(收个尾,可能这是最后一部分了QAQ)
Last. xyz约定(姿态角,"xyz convention")
这一种约定在研究飞机运动姿态时常用,而且对应的欧拉角也有自己的名称。
为更加形象,引入一张飞机的图片:
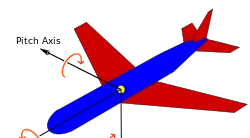
同样,旋转分为三步:
(1) 绕 z 轴转动 \phi 角;
(2) 绕第一次转动后的 y 轴转动 \theta 角(按惯例,该角 顺时针 为正,若严格按逆时针为正的话应为转动-\theta 角);
(3) 绕第二次转动后的 x 轴转动 \psi 角。
其中, \phi 称为 偏航角(yaw angle) ,\theta 称为 俯仰角(pitch angle) , \psi 称为 滚转角 (roll angle) 。
在上面的图中可以清晰看出这三个角的含义。
然后自然可以写出三步旋转的矩阵:
\bm{D}=\begin{pmatrix} \cos\phi &\sin\phi & \\ -\sin\phi & \cos\phi & \\ & & 1 \end{pmatrix}, \bm{C}=\begin{pmatrix} \cos\theta & & -\sin\theta\\ & 1 & \\ \sin\theta & & \cos\theta \end{pmatrix},\bm{B}=\begin{pmatrix} 1 & &\\ &\cos\psi &\sin\psi \\ &-\sin\psi & \cos\psi \\ \end{pmatrix}
以及合矩阵:
\bm{A}=\bm{B}\bm{C}\bm{D}=\begin{pmatrix} \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\cos\psi\sin\phi+\sin\psi\sin\theta\cos\phi & \cos\psi\cos\phi+\sin\psi\sin\theta\sin\phi & \cos\theta\sin\psi\\ \sin\psi\sin\theta+\cos\psi\sin\theta\cos\phi & -\sin\psi\cos\phi+\cos\psi\sin\theta\sin\phi & \cos\theta\cos\psi \end{pmatrix}
还有 \bm{Q} 矩阵:
\begin{aligned} \bm{Q}&=\begin{pmatrix} \cos\dfrac{\psi}2& i\sin\dfrac{\psi}2\\ i\sin\dfrac{\psi}2& \cos\dfrac{\psi}2 \end{pmatrix}\begin{pmatrix} \cos\dfrac{\theta}2& \sin\dfrac{\theta}2\\ - \sin\dfrac{\theta}2& \cos\dfrac{\theta}2 \end{pmatrix}\begin{pmatrix} e^{i\frac{\phi}2} & \\ & e^{-i\frac{\phi}2} \end{pmatrix}\\ &=\begin{pmatrix} \left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{i\frac{\phi}2} & \left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{-i\frac{\phi}2} \\ -\left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{i\frac{\phi}2} & \left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{-i\frac{\phi}2} \end{pmatrix}\end{aligned}
从中得到Cayley-Klein参量和Euler参量
\begin{cases} \alpha=\left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{i\frac{\phi}2}\\ \beta=\left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{-i\frac{\phi}2}\\ \gamma=-\left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{i\frac{\phi}2}\\ \delta=\left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{-i\frac{\phi}2} \end{cases}
\begin{cases} e_0=\cos\dfrac{\psi}2\cos\dfrac{\theta}2\cos\dfrac{\phi}2+\sin\dfrac{\psi}2\sin\dfrac{\theta}2\sin\dfrac{\phi}2\\ e_1=\sin\dfrac{\psi}2\cos\dfrac{\theta}2\cos\dfrac{\phi}2-\cos\dfrac{\psi}2\sin\dfrac{\theta}2\sin\dfrac{\phi}2\\ e_2=\cos\dfrac{\psi}2\sin\dfrac{\theta}2\cos\dfrac{\phi}2+\sin\dfrac{\psi}2\cos\dfrac{\theta}2\sin\dfrac{\phi}2\\ e_3=-\sin\dfrac{\psi}2\sin\dfrac{\theta}2\cos\dfrac{\phi}2+\cos\dfrac{\psi}2\cos\dfrac{\theta}2\sin\dfrac{\phi}2 \end{cases}
再考虑角速度变换。不难看出, \dot\phi 在空间 z 轴方向, \dot\theta 在第一次转动的后 y 轴方向, \dot\psi 在第二次转动后的x轴方向。从而不难写出角速度矢量的两种形式
在刚体坐标系 Ox'y'z' 下:
\begin{aligned} \bm{\omega}&=\bm{BCD}\begin{pmatrix} 0\\0\\1 \end{pmatrix}\dot\phi+\bm{B}\begin{pmatrix} 0\\1\\0\end{pmatrix}\dot{\theta}+\begin{pmatrix} 1\\0\\0\end{pmatrix}\dot\psi\\ &=\begin{pmatrix} \dot\psi-\dot\phi\sin\theta\\ \dot\theta\cos\psi+\dot\phi\cos\theta\sin\psi\\ -\dot\theta\sin\psi+\dot\phi\cos\theta\cos\psi \end{pmatrix} \end{aligned}
对于空间坐标系 Oxyz 下的角速度矢量,由于旋转过程的逆向过程分别是绕x,y,z轴,与原过程不一致,故仍需要用矩阵计算:
\begin{aligned} \bm{\omega}&=\begin{pmatrix} 0\\0\\1 \end{pmatrix}\dot\phi+\bm{B}^{-1}\begin{pmatrix} 0\\1\\0\end{pmatrix}\dot{\theta}+(\bm{BC})^{-1}\begin{pmatrix} 1\\0\\0\end{pmatrix}\dot\psi\\ &=\dot\phi+\bm{B}^T\begin{pmatrix} 0\\1\\0\end{pmatrix}\dot{\theta}+\bm{C}^T\bm{B}^T\begin{pmatrix} 1\\0\\0\end{pmatrix}\dot\psi\\\\ &=\begin{pmatrix} \psi\cos\theta\cos\phi-\dot\theta\sin\phi\\ \dot\psi\cos\theta\sin\phi+\dot\theta\cos\phi\\ \dot\phi-\dot\psi\sin\theta \end{pmatrix} \end{aligned}