我是几乎每次都考满分,要么就是稍微错个几分在145+的水平。后来碰上自主招生,去了几所985大学自主招生考试,考数学也都是满分。后来选的大学数学院副院长又和我是老乡,他直接打电话到我家里让我把志愿填过去。我也没有辜负他的期望,一路学习到博士。顺带提一句,不少人说浙江江苏卷145+很难考,但我当年就是浙江考生。
有一句话说得好,学霸考满分是因为只有这么几分能考。当年对我而言,数学是我的强势科目,确实是巴不得多个五十分上限。每次数学考试结束,所有同学都会来抢我的数学试卷来估分(只上交答题卷,我会在试卷上写好答案)甚至闹过一次乌龙,有一次一个选择题极难,我也考虑失误做错了,他们宁可相信是老师给的标准答案错了,也不愿意相信是我写错了。
我说一下我的看法。如果你平时成绩在某个分数左右波动,可以认为你的实力就在考那个分数的水平,但是如果你想次次都考满分,就至少得有个能考两百分的水平。换言之,成绩稳定在140左右和稳定在145+的同学,虽然只有不到十分的差距,但是知识的储备量至少相差了好几本书。
当我念高中的时候也会经常有同学来问我,为什么大家都来不及,而你却总是能考满分。于我而言,我觉得我每次成绩都考很好主要取决于以下方面:
①扎实的计算功底
正所谓「一力降十会」,在绝对的计算能力面前,所有的运算技巧、解题技巧都相形见绌。尤其是高考中的解析几何大题,基本没有任何思考量,纯粹地考察学生的计算能力。而在21世纪,计算数学甚至成为了数学系的四大主要分支之一。计算是数学中最根基的部分,只有计算能力强大,才能为你节约大量考试时间。目前应该除了上海高考外都禁止用计算器,而且即使上海考试有计算器的加持,强大的心算能力也是非常必要的。甚至你需要熟练使用小学时候学习的记忆20以内数的平方、2的10次以内的幂、3或者5的4次以内的幂、头同尾合十心算技巧等等。如何算得又快又对,虽然是小学时候就学的东西,但是终身受用。
②提前预习功课
我并没有提前太早学习新课,但是至少每个学期开始发新书的时候,我会抽一些晚自习的时间先把整个学期的数学书全部看一遍(其实所有学科的教科书我都这样干)全部看完并且理解以后,老师讲课的时候再听一遍,就相当于学习了两遍。
人们总说学霸总是不听课不做作业的,其实我想说不是。我虽然不听课,但作业还是要做的:因为看过一遍教科书,自己对着辅导练习册做做题就会了,没有必要再听课浪费时间。因此数学课对于我而言就是自修课,数学老师也跟班上同学说,要是跟我一样次次考满分,也可以不听课。
这个时间我并没有闲着。我会选择做一些竞赛题,当然也不是完全不听课,稍微听一些,觉得有趣的会自己做一些探究课题。
③题海战术,多做练习题
总有同学说,题型太多变了,每次学习了这个,他又换个题目考。我只能说做的题目还是太少了。高考不是竞赛,如果你刷的题足够多,你就能几乎做过所有高频的考点。
我高一就开始刷高考卷,刷到高考还在刷。高一的时候高考卷自测根本不及格,很多题都看不懂。但那又怎么样呢,做着做着就会了。到了高三正常考试的时候,基本就是手到擒来,而且很自信,做下去就对。
也就是说,不要在考试的时候去思考新的解法,思考方法的时间应该花在课后,而不是在考场上。真正的高分考生,基本就是看到一道题,就知道他在考察你什么知识点,也知道该用什么方法做。尝试一下,基本路就走通了,如果还走不通,再换个方法试试。
④不局限于教材,广泛地学习课外知识
在这里我想拿大家都能懂的鸡兔同笼问题举例子。
这是在我国国内非常著名的小学生奥赛题,基本所有受过奥赛培训的小学生都能熟练解出鸡兔同笼问题。但是他们用的方法,以及他们老师教学的方法,一般是这样的:假如所有动物都是鸡,那么少了几只脚,每把一只鸡换成一只兔,多两只脚,因此就能算出有多少只兔子,剩下的就全是鸡。
而对于初中生来说,鸡兔同笼问题是一个二元一次方程组问题,通过消元法可以快速计算鸡兔数目。
我想举这个例子来说明,对于数学题来说,解法并不一定是唯一的,甚至有些解法对于题目而言是「降维打击」的、是「秒杀」的。
也许看到一个要求计算线段比例的向量题目,中规中矩的方法要求建立基底一步步计算,甚至标准答案也会这么求解。但是如果你能熟练使用梅捏劳斯定理、塞瓦定理、斯特瓦尔特定理等这些竞赛书上有,教科书上根本没有的定理,你就会发现有时候一个填空题只需要十秒钟就能做完,甚至还不到十秒。在我自己考试时,我总是发现在选择填空上我就能比身边的同学快上二十分钟。
我同桌以前和我说,最紧张的一次考试是有一份四页的考试卷,他还在第一页做选择,我已经翻面做第三页大题了。
相信很多同学学习过「解三角形」这一节课。我们知道了在三角形中有正弦定理和余弦定理。但是课外的习题还有「非直角三角形△ABC中,tanA+tanB+tanC=tanAtanBtanC」这样的结论,也帮我快速解决过无数解三角形大题。
除此以外,我发现很多同学最希望听老师说的一句话就是「这个不考」,就把某个知识点一划,便再也不看。据我所知,在三角函数这一章节,很多省份不考积化和差、和差化积这两组共八个公式,还有万能公式、半角公式也并不在考纲里。但这些名词,即使不在考纲里,也很可能会出现在课堂上老师的口中:「我们讲一个从教材中删掉的重要知识点……」
但是对于我来说,在我的中学阶段,出于求知,我会把这些「额外」知识点自己单独推导至少一遍,而实践也证明了:若是真的考试用不上,任课老师为什么还要分出宝贵的课堂时间来讲这些东西?
有非常多的同学问过我,很多题目用传统解法做不出出来,而你又是怎么能够给出那么令人惊讶的破局思路和方法,你到底是怎么想到的?
我会回答说,那是因为我见得太多了。我会经常使用多种方法求解同一道练习题,这样在考场上我就有更多的思路来应对一道题。
举个例子,单是一道老师课上就不屑于讲解的基础的不等式练习题,我就能轻易想出十种以上的求解方法(如下图)


即使这是一道非常简单的例题,但这些解法背后所蕴含的道理却是格外深刻的,每一种方法都可以讲上好几节课的时间。而若想掌握其中最大的杀招拉格朗日乘数法,你必须在高中阶段自学掉整本高等数学和线性代数。在考场上,我只要从这么多的思路当中挑选出任意一种解出这道题,就已经足够了。
而到了博士阶段,也有不少中学生向我请教问题,出于对知识的敬畏,以及对那些先驱者的尊重,我也会严格要求那些学生们记住那些「不考,没用」的知识点。书上出现的著名定理,我还要求他们必须熟知是哪个国家的哪个数学家提出的。因为有一句格外打动我的话是这么说的:「你在课本上随手划下的一行公式,很可能就是某个人一生的全部工作。」
⑤做题习惯好
我在这里提到的做题习惯,主要指的是以下三个部分。
第一个指的是计算的时候心态好,耐心。
每一步计算时心态都很平静,不浮躁。写下每一个数字的时候都会顺手检查一遍有没有算错或者抄错。这一点在面对计算量巨大的题,尤其是坐标系下的立体几何题、解析几何题以及导数大题时尤为重要。不知道看到这里的小伙伴们有没有做大题时候算错了重算导致时间来不及的情况呢,我想应该是有的吧。
第二个指的是草稿工整
我的草稿是非常工整的。拍几张我最近计算时候书写的草稿



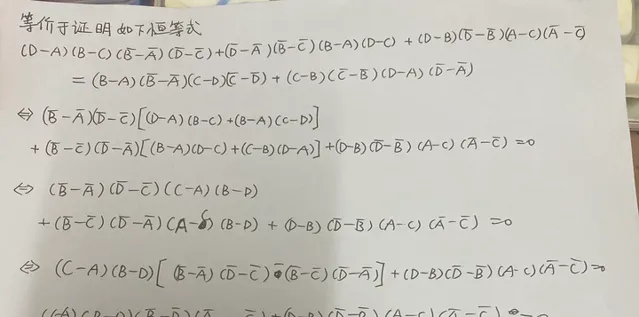
在多年前我的草稿就是如此,不会东一块西一块。这在考场上是十分有用的,基本上一眼就能看出来在哪一步算错了。如果没有带其他颜色的笔,我也会用黑笔把计算的关键步骤圈出来。
这个习惯为我做题节省了非常多的时间,尤其是检查的时候。
第三个指的是卷面工整整洁。
相信大家从我贴的草稿也可以想象到我考试卷面的工整整洁程度。如果说有个参照的话,我会提一下前几年很火的钱学森考试卷的例子

这是钱老的卷面,事实上在每次考试中我的卷面也是如此:合理的空间配置、工整的笔迹、以及着重标记关键步骤和答案等。
作为一个批改过高考卷的人,我可以很负责任地告诉大家这就是改卷老师想看到的卷面。
(下面这张图以及评论是我在发布回答两个月多月后更新的,这是我为我的学生制作的2023年中考解析)

你可以想象一下,如果你是阅卷老师,看到这样的卷面,心里会想什么。至少我会想,这样的学生就是满分的料子。帮他检查一下答案对不对,若是全对,我连过程都不想看了,直接给他满分。
事实上我确实依靠这样的方式在平时考试中骗到过分数,即使我的证明是错误的,但是阅卷老师根本没有细看就直接判了我对。甚至有过我蒙对了大题答案,过程几乎乱写,最后还拿满分的经历。(虽然不是很建议大家这么做)
而在黑板上书写板书的时候,我也会尽量写得工整清晰。

如果是教科书上没有的,我自己的备课稿件,我也会工整书写,并复印给学生使用。


一般来说,虽然高考数学,每个大题都有多种方法的多种给分方案,并且老师改卷只看给分关键步骤,答到点子上了,给多少分,没达到,就不给。
但是尽管有如此的步骤分评判方法,但是并不是卷面不影响成绩。对于阅卷老师而言,数学大题还是有轻微几分的自主裁量权的。这个主要体现在学生总是能够写出一些模棱两可的话,「说他对也有道理,说他不对也说得过去」这样的步骤,对应到某些学生「掌握了知识点,但没完全掌握」的状态。
相信无数的老师强调过:卷面是隐形的加分点。
这句话不是空穴来风。
当老师的这点都懂,这时候卷面的价值就来了。阅卷有一个不成文的规定,如果你的答案半对不对,与其在那里纠结半天你写得到底算不算对,要不要给你分,基本上就是看卷面,写得工整判你对,写得乱七八糟直接判错。
也许我和你写的内容都是一模一样的,但我就是因为卷面问题比你高两分,你觉得气不气。
在学校里,你可能还会因为自己「写的是3但长得像5被老师判错扣分」这件事耿耿于怀,找任课老师理论,但如果是中高考呢?
而在目前的阅卷制度下,你的一份卷子,会被按题目拆分,会被十几个人批阅——卷面的影响,会被放大至少十倍。说句不好听的话,如果你每道大题都写得模糊不清乱七八糟一片,每道大题偷偷扣你一两分卷面分,加起来十分就没了。更可怕的是,这还只是一门科目。
把字写工整,是对别人的尊重,也是对自己负责。这不是要求把字体书写得多么美观,多么艺术,只是要求你写的字能被人轻易认出来。
⑥合理规划时间
我并不是希望各位安排好多少时间做选择题,多少时间做填空,多少时间做大题,多少时间检查。这些都是会因为试卷难度有出入的。我要强调的一点是,不要在一道题上死磕。
哪怕是我这样次次考满分的人,我也会选择合理放弃一些题目,去先把分值更高的所有题目的分拿到手,再用剩下的时间回去死磕。
有些题,想不到就是想不到,分值又低,合理取舍是很重要的。之前陶平生出高考卷,最后一题全省无人做对。如果我参加了那场考试,我一定会在最后二十分钟的时候放弃这道题,用二十分钟时间把前面所有题目检查一遍。
⑦一定要留下时间检查
前面说到,合理取舍。但是对于我而言,每次考试时间都是比较宽裕的,两个小时的数学考试,我一般能够剩下30分钟甚至一个小时的时间来检查。如果是比较难的卷子,我也能至少留下十五分钟去检查。
主要原因是,在第一遍做的时候,有非常多的题目我总能挑选出我觉得最快速的解题方法去求解。而对于填空和选择题,有时候不需要太严谨的数学证明,有时候数学直观好,直接猜出图形的特殊位置、方程的特殊解、达到最值时候的取等条件等等,那就直接写上答案就行,回头做完卷子,还有时间再回来补充证明。
其次是,检查的时候根据剩余时间的多少,来确定检查方案。如果时间格外充裕,我检查一道题的方法是选择换一种新的方法重做这道题。这样做有一个好处,就是如果你用两种差别较大的方法在同一道题解出同样答案,那么可以直接断定你这道题就是做对了。因为两种不同方法解出相同答案的概率是极低的。但是这样的策略必须有一个前提条件:你得想得到两种解法(又或者说有的题目其实就只有一种解法)。如果检查的时间不够充裕或者说确实想不到新的解法,我会选择顺着一开始的解题步骤,一步一步重新算一遍。注意是重新写一遍而不是看着草稿看一遍。基本上你看一遍是看不太出错误的,也就是所谓的「检查不出来」。而如果你真的老老实实再去打一遍草稿,你就会很明显知道哪一步算错了。
我一般会预留20多分钟去检查,但是如果真的卷子特别难,时间没那么充裕,那我也会做好不整体检查的准备,但是相应地,我会告诉自己,之后每算一步都要很仔细。
⑧适当的「投机取巧」
曾经有同学问过我一道选择题,类似是f(x)≤a恒成立,求a的取值范围。
给了四个选项,分别是a>1,a≥1,a<1和a≤1
我告诉他说,这道题直接求解f(x)的最大值其实很难,但是如果我们观察到「如果对于某个a能满足这个不等式,那么比它大的所有a都应该被包括进去」
那么很显然,直接选择a≥1这个选项,因为如果它不对,其他选项就更不可能对。
这对于数学直觉好的同学来说是基本操作,但是这样的题目会让非常多「做题死板」的同学坑进去大量时间。
当然,对于高考而言几乎不可能出现这么显然的选项,但是在平时大大小小的模拟测验中,难免会出现这样选项质量不高的题,又或者就是为了锻炼学生「投机取巧」的能力而故意设置成这样的选项。
因此,就考试而言,掌握适当的应试解题技巧,也应该是学生们在学习过程中应该留意的一点。
⑨不要懒惰
我从本科一年级开始就开始做中学生家教,同时在校内也积极参加学工部的勤工俭学项目,为学校内其他院系数学功底薄弱的同学提供数学补习。
在我接触过大量的学生以后,我愈发觉得,孔子的「有教无类」是有道理的。当然在此基础上还有「师傅领进门,修行在个人」。
总有学生或是家长抱怨说,孩子智商不行,脑子不够灵光,学不了理科。于是我做过这样一个实验:我把数学书上重要的公式全部整理出来,其实每一章节也没几个公式,半页纸就能写下。我对学生说:「下次来上课,我会把这张纸上的知识点做成填空题,你完全不需要动脑子,你把它一模一样地、原封不动地默写下来。」学生觉得这任务很简单。
但是一周以后,默写效果总是 非常差 。
我再让他们回去记忆默写,依然 非常差 。
过了几周,我连这几个公式出现在教科书第几页第几行都记住了,学生还是默写不出来。
只有我说「若是默写不出来,那就不许下课,不许吃饭,直到默写出来为止。」的时候,即使是叫嚷着「完全不会」的学生,也能把所有知识点都默写出来了。
这也就说明了, 没有笨学生,只有懒学生 。
为什么总有人说题海战术有用?我觉得题海战术起码保证了一件事:反复巩固知识点。上课的时候看一遍公式,当场记住了,第二天就忘。而课后习题,每做一道题,就写一遍公式,连着做十题二十题,就相当于写十遍二十遍公式,真的会有人笨到简简单单一行公式,写上一百遍还记不住吗?
有一句大家耳熟能详的诗:「纸上得来终觉浅,绝知此事要躬行。」光是上课听老师讲解,看着书死记硬背的学习效果是很差的,不如自己推导一遍公式,做上几道典型例题。
在我给学生上课的过程中,我会经常询问学生,你们听懂了吗?得到的回答几乎都是:「听懂了。」而如果我让学生站起来回答问题,又或者仅仅是把我刚才说过的话原封不动复述一遍,他们就又会蹦出俩字「不会」。只有在我严格要求他们把板书抄下来作为笔记并当着我的面推导一遍,他们恍然大悟,说上一句:「哦!原来是这样啊!」我才能相信他们的确是掌握了。
老师上课讲过的内容,下课以后完全不复习,每天根本没花多少时间学习。平时周一到周五五天光顾着玩,就靠着周末的补习吊着一口气,两天打鱼五天晒网,每个周末补习的时候搞懂了知识点,到学校里去又只光顾着玩。到头来还要埋怨补习没效果、老师教学水平低、题目太难、自己太笨……找尽理由,就是不愿意承认自身的懒惰。这难道不是多数学生的真实写照吗?
只不过,我也认为不能把问题的根源简单归结为懒惰,它的背后还有更深层的原因。学生们年纪轻,并没有太多的阅历。我相信无数的同学,根本还没有搞懂「为什么要学习」这一问题。中学生也好,大学生也是如此。多数时候,限制一个人的并不是能力,而是态度。
不知不觉就写了这么多了,希望我的经验能对您有所帮助,谢谢。
距离上次回答已经过去两个半月了,期间收到了大家很多的看法,因此我再来补充一些吧。
Q1:中高考、自主招生这类考试,能用超纲的方法解题吗?
A1:能。就一点: 做出来比不会做强 。
我甚至巴不得学生发明一种我看不懂的方法来解题。
只要你熟练掌握了正确的知识,那就大胆地去使用。
但前提是你得 ①使用了正确的方法②解出了正确的答案③规范地书写解答
老有学生说:我用了某某方法某某定理,结果没有步骤分了。
我把卷子拿来一看,分明就是定理都背错了。
很多老师不建议学生使用超纲方法答题的根本原因就是,学生们对这些知识没有经过系统的训练,基本都是稀里糊涂乱用的。多数情况并不是「使用了超纲知识被扣分了」,反而是「你以为你用了正确的方法,实际上用错了」
看到数列就求极限的,极限的存在性证了吗?没证的,扣分。上来就给未知函数求导要么积分的,可微性证了吗,可积性证了吗?没写的,扣分。
就阅卷而言,即使你在卷子上把哥德巴赫猜想证出来了,题没做对,没分。
这里我讲一个令我印象深刻的故事。
有一年我参加大学的自主招生阅卷工作,考生多为高中学生,压轴大题是证明一个方程无解。
试评完发现考生们主要使用两种方法:
多数学生使用的第一种方法中规中矩,构造函数求 n 次导数,分奇偶讨论单调性,步骤繁琐,需要书写整整一页。
少部分学生使用的第二种方法是使用泰勒公式,将题目给的函数展开至 n 阶。
泰勒公式是超纲的公式,因此我们在试评的时候发现卷子上凡是使用泰勒公式的同学都是一知半解的,所有使用泰勒公式的同学,都在展开完以后使用了佩亚诺型余项,但是佩亚诺型余项无法证明方程无解。
因此阅卷组长通知, 凡是使用泰勒公式解题的同学,一律判为0分 。
我改着卷子的时候,突然一份答案呈现在我的眼前,字迹清秀但却只有寥寥两行。
我的第一印象就是答卷没写得密密麻麻的,基本就是不会的,何况又是这种只写了两行的答案呢。想着等会儿给他0分,但还是仔细查看了他写的这两行过程。
第一行:「使用 带拉格朗日型余项的泰勒公式 在 x=0 处展开至 n 阶,其中 \xi 介于 0 和 x 之间 ,故由余项非零知方程无解,得证。」
第二行则是余项的公式。
我当场举手示意:「组长,这里有个用泰勒的,可他是对的!」
教授过来看了一眼说了两句话,第一句是「给他满分」,第二句是「这样的同学就是我们想要的。」
我这里给大家解释一下:寥寥两行文字,但全是精炼的术语,没有半点废话。而能够精确地使用带拉格朗日型余项的泰勒公式,则说明他至少精读过高等数学的教材,而不是囫囵吞枣地翻看过。
戏剧般的剧情,两行证明,满分到手。
结合以上,我的建议就是,我不排斥学生使用超纲方法解题,但学生很可能因为掌握得不够彻底、不够专业、甚至因为使用错误而有扣分风险。所以我也总是对学生们说, 除非你真的想不出课内的方法,那么就用超纲的方法先把答案做出来。
超纲方法做对了,好歹是能拿到分的。不超纲方法死活想不到,做不出来可是一分都没有的。
我在高中阶段考过无数次的多校联考数学单科第一名,有些大题,尤其压轴题的数列或者导数不等式就是靠微积分解出来的。题目本身就难,得分率低老师改卷就仁慈,哪里还会抠那么多的细节,把答案做对就直接给你满分了,而这种时候我的竞争对手都没做出压轴题。
有同学表示自己平时使用非主流方法总被老师判错,对此我的评价则是:水平越低的老师,思想就越是僵化。数学这门学科,只有好的方法、差的方法,没有一定要使用的标准方法。
考试越是大型,就越应该大胆地去使用——放心,阅卷老师的水平高得很,只要你的办法是对的,你一定能拿到该拿的分数。
阅卷老师心里清楚, 没有任何理由淘汰一个优秀的同学 。
Q2:评论区不少人说,学习还是得看天赋,我对这句话讲讲我的看法吧。
A2:你们知道在顶级学府里面最让人绝望的一点是什么吗,那就是比你聪明的人却比你更努力。而现实生活中从小学到大学这样的例子比比皆是,只是很多人步入社会以后才意识到这一点。说个老梗吧,科比被问到「你为什么如此成功」时说:「你们见过凌晨四点的洛杉矶吗。」
天赋因人而异,努力总不是因人而异的。在一些高中,你甚至能在正月初二就看见里面坐着零星的自愿来学习的同学。如果你问我为什么知道,我会告诉你因为我当年就是其中之一。
诚然,即使不说天赋,不同地方也有着巨大的教育资源差异。就初中教师而言,有的是专业的教育博士,有的却自己都没搞懂教材便给学生讲课。「千里马常有,而伯乐不常有。」有好天赋还不够,还得有好老师。这些客观差距就是无法弥补的。
但若是有人大放厥词,喊勤奋无用——骗别人可以,别骗自己了吧。
Q3:我看评论区有人说,有天赋的人看东西一看就懂,没天赋的人看一百遍也看不懂。
A3:这一点其实我也想讲一个故事。
我初中的时候很喜欢玩计算器,就看到计算器上有很多乱七八糟的功能,不少我能看懂,但也有一些我看不懂的,尤其是卡西欧计算器右上角的 \int 记号。
我就和周围同学开始研究啊,这东西到底是什么意思。结果有次下课一个同学很兴奋跑来找我说,我明白了, \int_{a}^{b}kdx 的意思就是「上面的减去下面的再乘以中间的」。
我按了几次发现是对的,也就是 \int_{a}^{b}kdx=k(b-a) 但疑问也随之而来:这么简单的计算,难道还值得人们发明一个专门的记号来表示吗?
实在想不明白,还是决定去问老师了,老师看了一眼说:「这个是微积分啊,大学里面学的。」
但我没有就此打住,而是追问老师:「老师,我能学吗?」
老师撂下一句「你现在还学不懂吧」就离开了。
我回家以后不是很服气,上网查了一通,没看懂。
碰巧我妈当时觉得我英语不好,在家边上给我找了个大学生家教补习英语,我记得是个二本院校的文科女大学生(非常典型的数学很差的类型)。当时她应该是快期末考试了,给我补习的空档还拿着一本微积分的书复习。我偷瞄了一眼,这书里全是 \int 记号!
我当时就来劲了,我跟她说,你的这本书可以借我看看么?
她说可以啊,便把书递给我。书名我忘了,大抵是所谓【微积分教程(文科专业用)】之类的。我翻了翻,便不太情愿地还给她了。
她见我如此有兴趣,便随口说道:「你要是想看,这本可以送你,我回去再买一本就是了,学校旧书摊里这些书多得是。」
因此我便得到了我视若珍宝的人生中的第一本微积分的教材,虽然它到我手里的时候已经很旧了。
我特别爱那本书,可是我根本看不懂。
但这本书是我的,一遍看不懂我可以看两遍,两遍看不懂我可以看三遍。
老师同学那时都对着我笑,说我要走火入魔了。
我也忘了我到底翻过几遍那本书,但是我去哪里都要带着它,即使看不懂也对着它发呆。若是真的大致说个数的话,至少得有个几百遍。本来书就有点破旧,后来书的封皮都被我翻得整个掉下来了。
我只记得在某个晚自习我突然好像如醍醐灌顶,猛地一下顿悟——突然就看懂了。
那一刻我欣喜若狂,赶紧翻回第一页重新往后看,果然每一页都能看懂了。
古人有云:书读百遍,其义自见。
至此,我有关 \int 的疑问全部消除。
而公式\int_{a}^{b}kdx=k(b-a) 也在这一刻升级成了 \int_{a}^{b}f(x)dx=F(b)-F(a)
微积分基本定理——人类历史上最伟大的公式之一。
几天后初中课堂的数学课,恰好在讲动点求面积最大值的中考压轴专题。别的同学在那闷头苦算,而我看了一眼就觉得直线和抛物线相切的时候面积最大……等等,相切……前不久刚看懂的微积分书里不就教了怎么算切线吗?!把微积分应用到初中题目一做,完全就是秒杀,连我自己都惊呆了,居然题目还可以这么做。用现在的话来说,这叫「降维打击」。
再后来我就发现,原来这本书讲得这么简单。(毕竟是文科专业用书)
后来上了高中,则是理工科用的微积分教材,甚至数学专业用的数学分析了,而看后面这些书带给我的震撼,远没有那本破书来得巨大。
我想这就是哲学里面所谓的量变引起质变吧。
我不觉得一本高中的教科书真的有人「看一百遍也看不懂」,我觉得看不到一百遍,甚至看不到十遍的可能性更大一些。毫不夸张地说,无数多的学生,即使已经毕业了,却连教科书都没有完整地阅读过一遍,更别提课外书了。
行百里者半九十,若是真能做到下定决定看上一百遍,我想大抵还是能看懂的吧。
要是还不行,那就看一百零一遍试试?
万一真看懂了呢。
书中自有黄金屋,书中自有颜如玉。——读书人的快乐,也便在这两句诗之中了。










