方差是什么意思以及怎么算？

方差是什么意思 ?

频率的随机起伏是一个随机变量，是时间t的随机函数，不可能测量其瞬时值，实际测量获得的是有限时间段内的平均值。

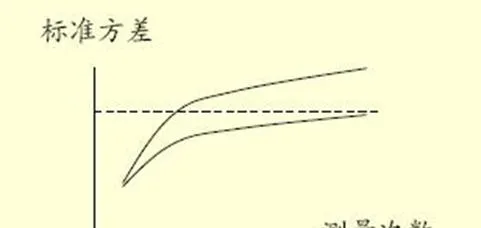
标准方差随观测次数是变化的，对平稳过程它是收敛的，对非平稳过程，它是发散的。

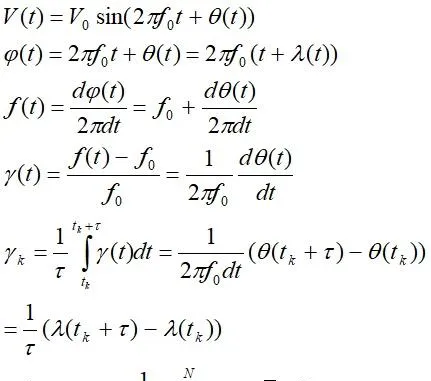
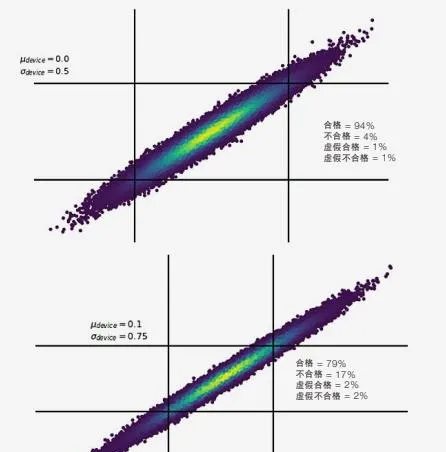
我们一信号源为例，频率稳定度是信号源最为重要的技术指标。相位噪声谱密度是频率稳定度在频域内的测度。时域内的测度，一般是根据误差理论，用随机误差的标准方差（精度）来表征稳定度.

由于信源噪声包含有非平稳随机过程，用标准方差表征稳定度存在着不收敛问题（对随机游走调频噪声和调频闪烁噪声两种噪声，标准方差不收敛），因而一般采用Allan方差作为频率稳定度的时域测度。

阿伦方差

信号源噪声中含有闪变噪声，标准方差无极限收敛存在，测量次数越多，标准方差的估计偏差越大，是一个不确定表征量。为了克服这个问题，用阿伦方差来表征信源的噪声时域特性。

阿伦方差：以相对频率起伏的取样方差为基础，两次取样方差的时间平均称为时域的频率稳定度测度。

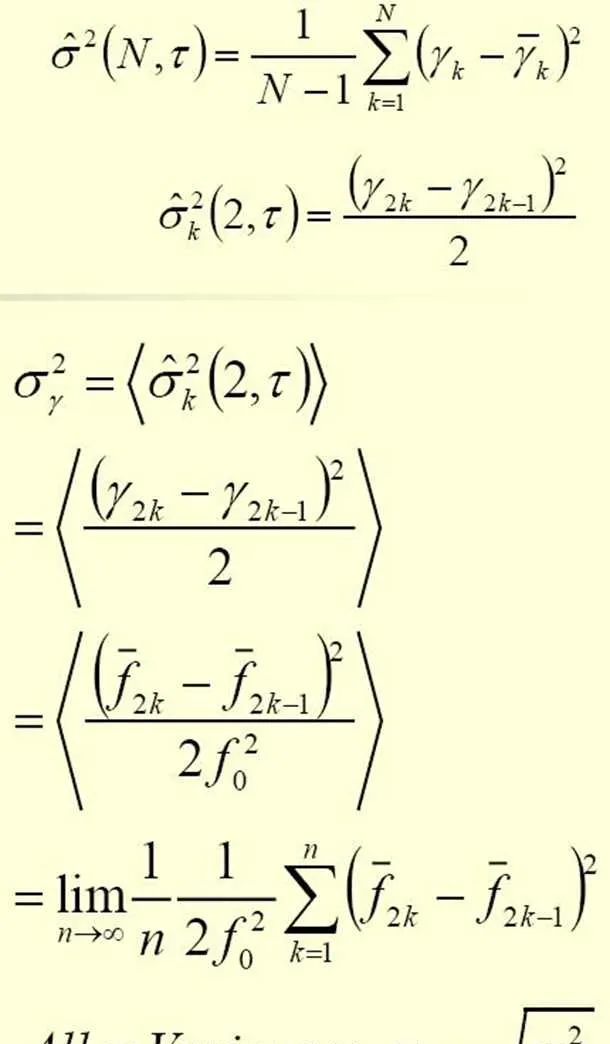
Allen阿伦方差和观测时间

阿伦方差对五种噪声类型全部收敛，并且可以从和观测时间τ的关系来判断噪声类型

除了调相白噪声和调相闪烁噪声外，噪声类型和观测时间τ有一一对应的关系

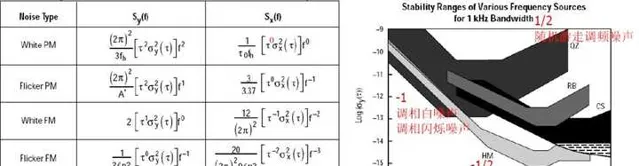
信号源能提供对频率源最完整的测试分析功能。测试功能包含：相位噪声，阿仑方差，频谱杂散测试，信号功率，信号频率，VCO压控特性，频率源跳频过程分析，信号调幅噪声，基带信号分析等。

抖动分析功能分析测量方差随时间的变化情况。抖动分析使用的主要测量是时间 间隔错误 (TIE)，但也可以分析多个其他测量。

推荐阅读：

「随机抖动分量它是所有会影响信号质量的随机噪声源的总和。由于我们是假设随机抖动呈现高斯分布，并用高斯分布的平均值和标准方差来定义随机抖动。若要确定随机噪声源产生的抖动，必须确定和评估代表这种随机抖动的高斯函数和它的标准方差。」

是德科技不相关输入量的不确定度分析和韦尔奇-萨特思韦特公式的一般规则

摘要

测量不确定度表示指南 (GUM)已经广泛应用在工业和科学的各个领域。该指南建立了一套评估和表示测量不确定度的基本原则。本文将会概述如何使用该指南表示不相关输入量。本文还会介绍与测量不确定度评估有关的相关量值和类型，不同量之间的相关性是产生测量不确定度的原因。我们将会识别未包含在 GUM中的情况，其中被测变量可以表示为随着带有共源的数量而变化。当测量误差不具备有限自由度且不相关时，我们使用典型的韦尔奇 -萨特思韦特公式来计算自由度的有效数，就会出现问题。我们还会介绍韦尔奇 -萨特思韦特公式的一般规则，针对的是具备有限自由度的相关成分。

本文还将介绍其它用于计算置信限制和扩展不确定度的方法，例如基于卷积的数学方法，或使用蒙特卡罗仿真在传递概率分布的基础上评估测量不确定度。

通常，测量结果并不是直接测得的，而是通过其它量和函数关系而获得:
Y= f (X1,X2,X3...Xn)
假设输入量是独立的，合并标准不确定度是合并方差的正平方根，如下所示: 输入量可以表示为协方差系数或相关系数，应用在传递时。

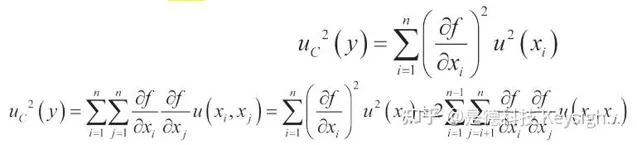
xi 和 xj 的相关度可由估计出的相关系数表示。

使输出估计值的标准不确定度乘以包含因子 k(在指定置信度的基础上选择 )，可以获得测量扩展不确定度:

U = k * Uc (y )

当被测量呈现正态分布，且输出估计值的标准不确定度具有足够的可靠性时，应当使用标准包含因子 k = 2。

根据中心极限定理，假设总误差遵循正态 (无限自由度 )或学生 t分布 (有限自由度)。

该定理表明了 :总误差分布会随着成分误差数目的增加而会敛于正态分布，不考虑它们的潜在分布 (图 1)。

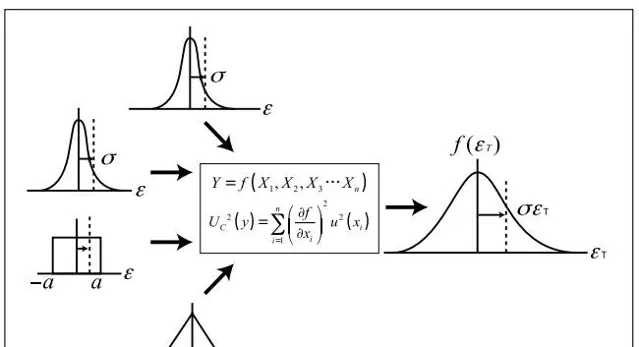
会图 1. 总误差分布

确定置信度的扩展不确定度的首个方法是使用正态分布的包含因子 k:

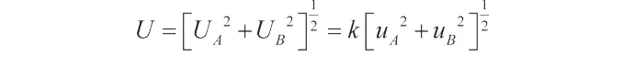
如果随机读数较小，那么 uA值可能有误，随机分量分布更适合通过学生 t分布来表示。但是我们现在能够对不确定度估计一个高值，尤其是在测量次数较少且 uA和 uB值类似的情况下。

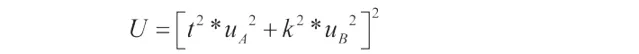
最佳解决方法是韦尔奇-萨特思韦特公式。

假设是正态分布，但输出估计值的标准不确定度没有足够的可靠性，重复测量的次数也不可能增加，那么我们需要使用韦尔奇 -萨特思韦特公式。在这种情况下，输出估计值的标准不确定度由其有效自由度决定。

以 n独立测量误差的直接测量为例，误差分布类似于 t分布，且利用韦尔奇 -萨特思韦特公式获得其有效自由度 ν eff :

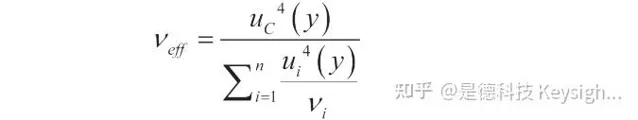
通过学生 t 分布可以获得包含因子 k (p ) ，在覆盖率为 95.45 % 时测得。

3. 正态分布不可调整

当正态分布不支持调整且无法应用中心极限定理时，我们会发现预算中的一个或两个不确定度分量可作为主项。

我们可以借助分布密度φ (y) 和以下积分关系式来确定覆盖率 p :

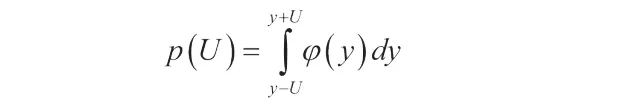
包含因子可表示为:

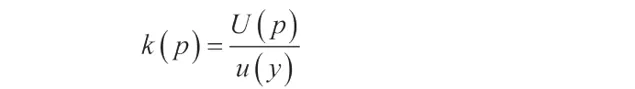
3.1 矩形分布作为主项:

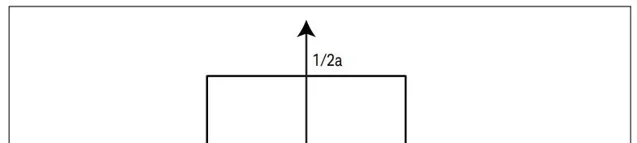
求解这个关系式可以得到扩展不确定度 U ，把结果与标准测量不确定度表示结合在一起 (与矩形分布有关):

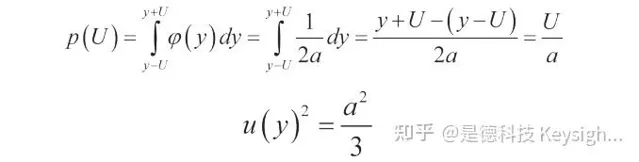
给出关系式:

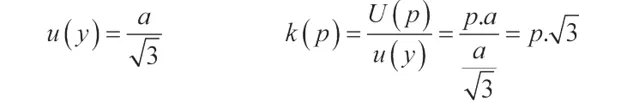
覆盖率 p = 95% 时，包含因子 k 为:

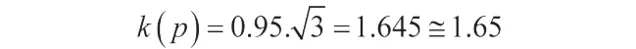
3.2 预算中的两个不确定度分量可作为主项。

这将涉及在卷积分布的情况下，对规定覆盖率的包含因子进行评估。

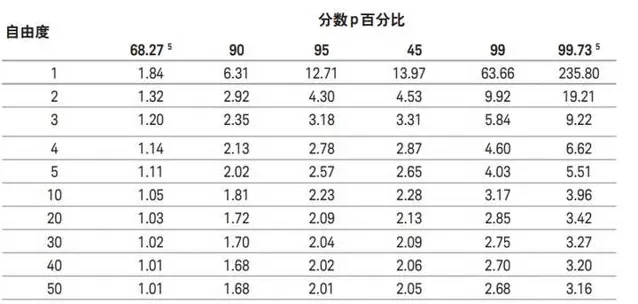
根据卷积的分布类型，覆盖率为 95.45 %时的包含因子可通过表 1中的指定比率获得:

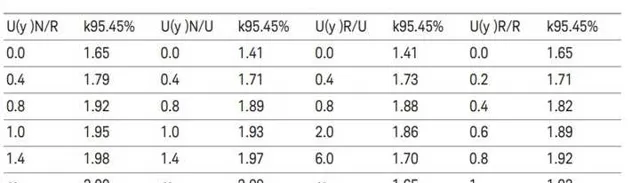
表 1. 假设两个分布呈现卷积, 包含因子 k可通过下表获得

4. 使用卷积来获得总误差分布

当两个或多个误差与统计无关时，可使用卷积来获得总误差分布。该方法适用于直接测量，测量过程中的误差与统计无关，也不必进行误差修正。

4.1 两个矩形分布的卷积:

如果主要分量来自于数值的矩形分布，卷积所得到的分布会呈现对称梯形分布 (图 3)。

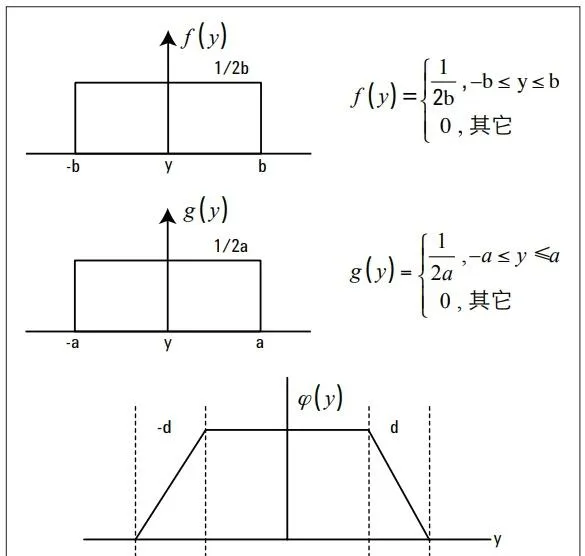
其中，底部和顶部的半宽分别是: c = b + a 和d = |b - a | 和边沿参数:

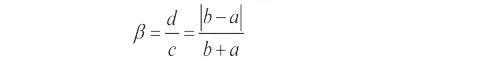
其中，分布密度可以表示为:

从梯形分布中推导出的标准测量不确定度的平方值是:

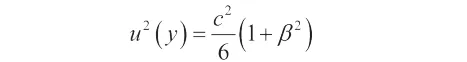
覆盖率为:

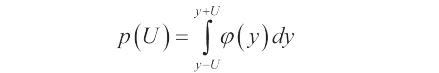
包含因子

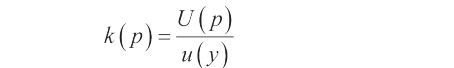
包含因子将会是:

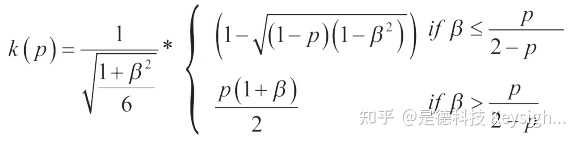
最后，根据下面的关系式计算出覆盖率为 95 %时的包含因子 (在边沿参数 β < 0.95 时的梯形分布中):

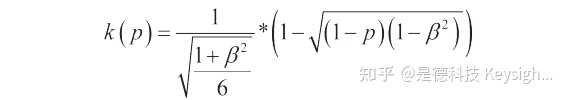
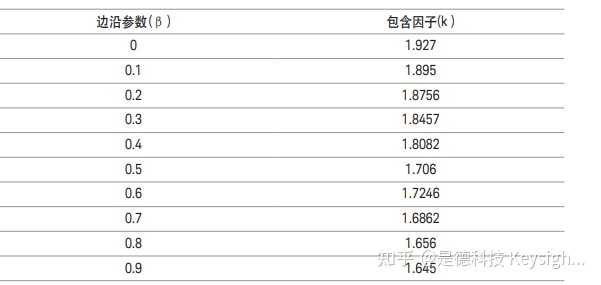
K (p) 可在 1.645 至 1.93 之间变化，取决于β。 (表 2 和图 4)

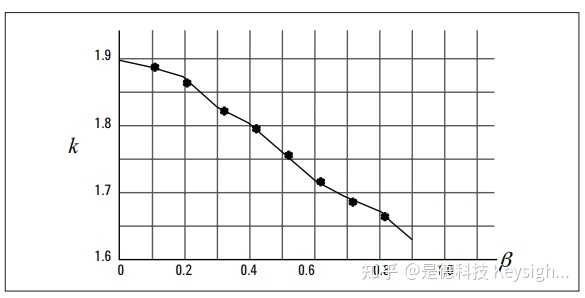
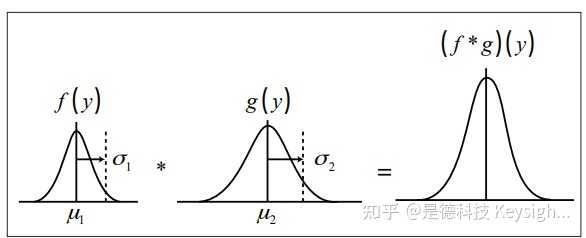
4.2 两个高斯分布的卷积

总误差分布采取高斯形式 (图 5)。

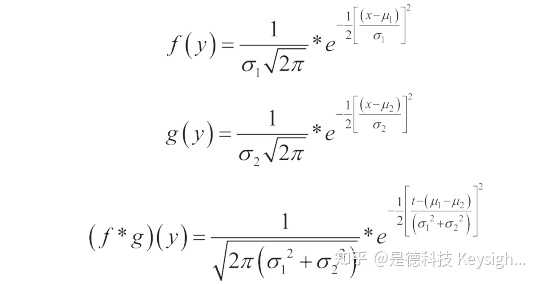
5. 针对相关成分的韦尔奇-萨特思韦特公式

GUM的实施会遇到有效自由度问题，其中被测值可表示为随中间量 (取决于一个或多个共享输入 )而变化的值。很明显的是，零的直线相关系数并不意味着统计独立性。因此，变量不是独立值 (除非是标称值 )，自由度都是有限的。这与韦尔奇 -萨特思韦特公式的使用没有特定关系，而是源于统计方法的含糊使用和不完全使用。

我们将把 GUM中描述的方法扩展到具备有限自由度的不确定度的相关成分。在这种情况下，我们使用由 Howard Castrup建议的韦尔奇 -萨特思韦特公式

考虑两个测量误差 e1和 e2，不确定度分别是 u1和 u2，相关系数为 ρ 12，总误差的方差是:

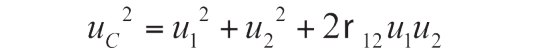
使用加法规则，可以得到

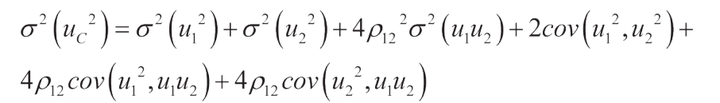
使用向量积和协方差，我们得到以下表达式:

应用在n 测量误差(有两个或多个相关误差)，

用于相关成分的有效自由度计算的表达式为:

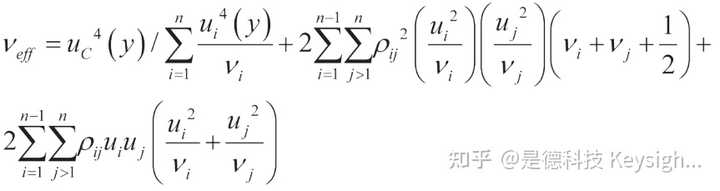
假设所有的相关系数为零，这个等式简化为韦尔奇-萨特思韦特公式。

6. 使用蒙特卡罗仿真处理传递概率分布

当模型是非线性或输出量的概率密度分布函数 (PDF)背离高斯分布或缩放和转移学生 t分布时，我们需要使用蒙特卡罗法 (MCM)。该方法能够处理输入量的传递概率分布。

在测量模型等式中，通过使用分布函数 G，MCM可获得恰当的输出量 Y数值表示。通过采样输入量 xi 的 PDF 并应用测量模型，可以得到 G ，进而得到输出量 Y 的采样值。可从 G 中提取期望值、方差和 Y 的有效区间。

G的精度随着实验次数而提高。自适应蒙特卡罗法不必通过固定次数的实验来担保测试结果具有指定容限。实施更多次数的蒙特卡罗实验，直至平均值、方差和有效区间达到稳定。如果标准偏差的两倍值小于标准不确定度 u(y)的数值容限，这个数值结果被视为稳定。

7. 学习目标

本文描述了根据 GUM中针对不相关输入量的原则，对测量不确定度进行评估的方法，涵盖了无法应用中心极限理论的情况。本文采用韦尔奇 -萨特思韦特公式的一般规则，把该方法扩展到具备有限自由度的不确定度的相关成分。

针对所有的量都已关联且正态分布的情况，本文最后还介绍了另一种方法。当未能达到 GUM的应用要求时，蒙特卡罗法可用于计算不确定度，对 GUM提供的结果进行验证并获得置信度。只要所有的量均已相关，且呈现正态分布或完全相关，蒙特卡罗法就能处理相关性。实际上，当相关量的分布明显不同于正态分布时，该方法存在一个限制。通常情况下，无法针对输入变量指定 PDF，也很难对 PDF 进行数值仿真。

是德科技