什么是方差
方差是衡量一组变量离散程度的度量,方差越大波动越大,方差越小,波动越小。
方差计算公式
S^{2}=\frac{\sum(X-\bar{X})^{2}}{n-1}
S^{2} 为样本方差, X 为变量, \bar{X} 为样本均值, n为样本例数。
SPSSAU方差分析
方差分析 就是通过检验各总体的均值是否相等来判断X(定类)对Y(定量)的影响。例如:想要研究三个行业之间服务质量是否有差异。
方差分析操作路径
【通用方法】→【方差】
进行方差分析的数据需要满足正态性检验以及方差齐性检验。
正态性检验
以SPSSAU为例,结果如下:

由于样本量为20小于50,所以利用S-W检验,发现p值为0.07大于0.05,所以数据满足正态性。
SPSSAU分析建议:

方差齐性检验

从上表可以看出p值为0.31大于0.05,说明没有显著性,数据波动一致,满足方差齐性,可以使用方差分析。
SPSSAU操作与说明
SPSSAU操作
结果

从结果中可以看出F值为24.55,p值小于0.05,说明具有显著性差异,不同口味之间的销售额有显著性差异。
指标计算

方差分析用于研究差异,差异共由两部分组成,分别是组间平方和,组内平方和。
(1)自由度
组间自由度df 1=组别数量 – 1;该案例中组别为4,组间自由度:4-1=3;
组内自由度df 2 = 样本量 – 组别数量;该案例中样本量为20,组内自由度:20-4=16;
(2)均方
组间均方 = 组间平方和 / 组间自由度df 1;
组间均方:0.74/3=0.2455≈0.25;
组内均方 = 组内平方和 / 组内自由度df 2;
组内均方:0.16/16=0.01
(3)F
F值=组间均方 / 组内均方;F值:0.2455/0.01=24.55;
除此之外SPSSAU还提供折线图进行对比
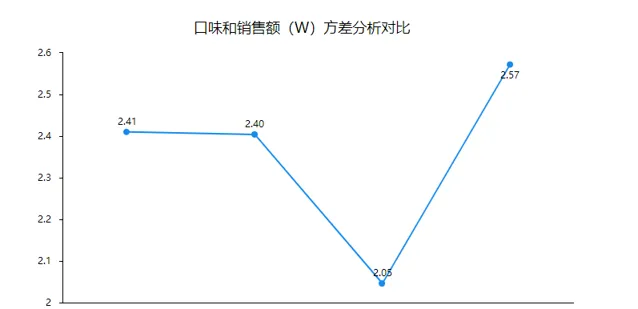
从图中可以直观的查看到水果糖D的销售额平均水平更高一些,水果糖C的销售额相对较低。
SPSSAU比SPSS提供更多便捷的结果,并且操作更简单,所以可以选择SPSSAU进行分析。











