我来主要谈一谈 微分拓扑学 在数理经济学中的应用。
德布鲁教授在诺贝尔经济学奖的获奖演说中,提到过大数学家S.Smale(斯梅尔,没错就是非线性泛函分析中著名的Palais.Smale条件的斯梅尔,著名的微分拓扑学家,主要研究动力系统)向他介绍过一个重要的定理——Sard定理及其拓展:横截-稠密性定理。横截性的抽象定义如下:
横截-稠密性定理:假设 Z\subset N 为 s 维光滑流形,称映射 f:M\rightarrow N 横截于 Z ,指下式成立:
df(x)(T_{x}M)\oplus T_{f(x)}Z=T_{f(x)}N 。
很多人可能光看定义头都大了(其实这个定义有很直观的几何意义)。在这里我不想过多地去谈所谓横截性的抽象定义, 我直接翻译成初等微积分的语言 ,相信都能看懂:
假设有 M 个(非线性的)方程, N 个未知数,组成的方程组:
f^{1}(v_{1},v_{2}...v_{N};q_{1},q_{2}...q_{S})=0\\ ......\\ f^{M}(v_{1},v_{2}...v_{N};q_{1},q_{2}...q_{S})=0
或者缩写成 f(v;q)=0 ,其中 q 是 S 个参数。 横截-稠密性定理说的是 :
如果当 f(v;q)=0 时, M\times (N+S) 维矩阵的秩 rank Df(v;q) 为 M (行满秩的),那么对于 几乎(按Lebesgue测度)所有的 q ,当给定这个 q 之后(比如 q=\bar{q} ), M\times N 矩阵 D_{v}f(v;q) 的秩也为 M 。
这跟经济学有什么关系呢?在进行大范围分析的时候,我们总是把经济的初始禀赋 w 作为参数。我们需要证明,对于几乎所有的初始禀赋,经济都是正则的!(经济正则的重要意义后面会讲述)
给定经济体中第 i 个人对第 h 种商品的 超额需求函数:
z_{h}^{i}(p,w)=x_{i}^{h}(p,pw^{i}-w_{h}^{i}) ,那么第 h 种商品的 总超额需求函数 为 :
Z_{h}(p,w)=\sum_{i=1}^{n}x_{h}^{i}(p,pw^{i}-w_{h}^{i})
从而 整个经济体 的 总超额需求函数 为 C^{1} 映射 Z=[Z_{1}...Z_{h}...Z_{L-1}] 。根据我前面说的横截性定理,我们可以证明对于几乎所有的初始禀赋 w ,经济都是 正则 的。
由于价格球体的正象限部分是紧的,因此,根据反函数定理,任何正则经济都有有限个均衡点,使得超额需求 z(p)=0 ,即市场出清。
正则经济之所以重要,一个关键点是在于我们可以进行指数分析,所谓指数,直观理解,我们首先从一维开始:
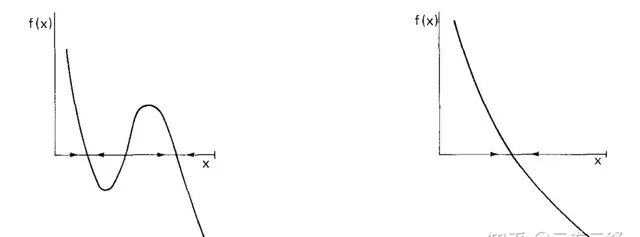
当价格(横坐标)很小的时候,超额需求(纵坐标)为正,当价格很高时,超额需求(纵坐标)为负。这是非常一般的假设,也非常符合常识。也就是说, 超额需求是指向区间内的(这个边界条件非常重要!!!!!!!!) 。问题是我们如何通过这一最最普遍的假设入手,分析市场动力学的定性行为呢?
对于 高维空间的指数,也有非常直观的画面演示, 可以参考我的另一篇回答:
(Poincare-Hopf定理) 设N 是一个n 维紧致 带边光滑流形 ,f 为其上的光滑向量场,具有有限个零点。若对于\forall x\in\partial N ,有f(x)\cdot g(x) 为正(其中g(x) 为超曲面\partial N 的Gauss映射), 也就是说,要求向量场在流形边界处指向外。 则该动态系统的指数和等于流形N 的欧拉示性数\chi(N) 。
我们刚刚说过,超额需求是指向区间内的。因此我们需要把向量场乘以负号(翻转过来)以满足定理的要求,因此就有:


注: 欧拉示性数\chi(D^{n}的正象限部分)=1 。(因为与 单点同伦! )。同时要使用Poincare-Hopf 定理,只有对正则经济才有效,所以横截-稠密性定理才那么重要!











