文@ 小P家的021419
0 前言
在模型实际的业务落地过程中,大家是否遇到过这样的场景:千辛万苦训练出了精度满足业务需求的模型,终于可以上线啦!经过模型转换、量化、打包等等一系列复杂的流程后,成功部署到实际硬件平台上,模型终于可以运行了!然而一波操作猛如虎,模型精度与当初训练结果相比却下降了不少……一脸茫然,不知所措,完全不知该从何下手,也不知道怎样才能有效的恢复模型的训练精度。 本次分享将针对部署流程中导致精度下降的头号疑犯——模型量化进行分析,带大家一探精度损失的幕后真相。
本文将从以下三个方面进行「揭秘」: - 量化的基本过程 - 量化的损失来源 - 常见芯片的量化支持
1 量化的基本过程
模型量化粗略地可以分为在线量化(Quantization Aware Training, QAT)和离线量化(Post Training Quantization, PTQ)两大类。 虽然在线量化可以对量化后的模型精度提供更高的保障,但因其与模型的训练过程过于耦合,开发成本和门槛较高,在模型部署阶段采用更多的是另一种方式——离线量化。因此,本文主要针对采用离线量化方式对模型量化后,产生的精度损失进行分析。

神经网络的量化本质上是将数据从连续空间 \mathbb{C} 映射到离散空间 \mathbb{D} ,这个过程通常包括三个阶段: 数据缩放(scale),数据离散化(discretize),数据反向缩放(rescale) 。 三个阶段之间关系的可以形式化描述如下:
Q(x) = f^{-1}(round(f(x)))
输入数据 x 是来自连续空间 \mathbb{C} 的全精度值,即原始的浮点精度表示数据, Q(x) 是量化后在离散空间 \mathbb{D} 中的对应值,即定点类型的数据。 首先,缩放函数 f(\cdot) 将数据 x 从原始空间 \mathbb{C} 的表示范围缩放到离散空间 \mathbb{D} 。 然后,缩放后所得到的数据被离散化为属于离散空间 \mathbb{D} 内的中间值 z ,该阶段最常用的离散函数是 round(\cdot) 。 最后,因为量化操作只改变数据的表示精度,不更改数据的表示范围,所以离散化后的中间值 z 需要使用反向缩放函数 f^{-1}(\cdot) ,重新调整 z 到与 x 在原始空间 \mathbb{C} 中相同的表示范围。在不同的量化方法中,数据缩放函数和数据离散函数各不相同。
当前较为成熟且使用较多的量化机制为线性均匀量化,指缩放函数 f(\cdot) 为线性映射函数,离散空间 \mathbb{D} 中的各个离散值之间的距离是均匀的。如使用的是线性量化,原始数据 x 的数值表示范围为 [\alpha, \beta] ,缩放函数可以表示为:
f(x) = scale_{factor} * clip(x, \alpha, \beta) + zero_{point}
在对称量化中, zero_{point} 设置为 0,同时要求 -\alpha = \beta ;在非对称量化中,zero_{point} 会根据实际的数据范围进行确定,通常会选取 zero_{point} = round(\frac{\alpha + \beta}{2}) 。
2 量化的损失来源
实际部署过程中,为了获得更大的压缩率和更快的运行速度,或受限于部署平台的计算单元类型,模型通常需要对整个网络模型的权值和激活值均进行定点量化。为了简化讨论,我们以一层卷积作为示例,采用线性均匀量化的方法,并假设 bias 已经通过优化融合到了 conv 的 weight 中。如下图所示,整层网络的计算误差主要来自于三部分:
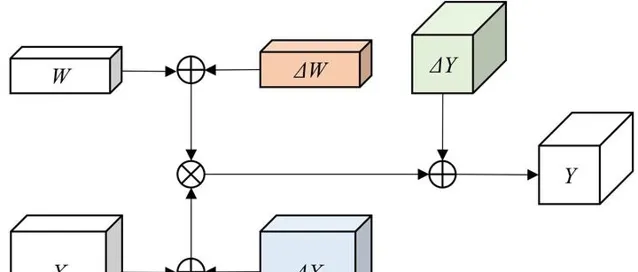
为了进一步考虑上述误差是如何在计算过程中引入的,我们固定量化的比特位数 N 。根据量化的三个计算阶段我们可以看到,均匀线性量化过程中涉及到的可能引入误差的操作主要有三个: Round 操作,Clip 操作,scaling factor 的选取 。Round 和 Clip 操作引入的即为前文所指的各类取整和溢出误差,不同的线性均匀量化方法和优化策略本质上即为不同 scaling factor 的选取。三者对误差的引入和影响是紧耦合在一起的,互相作用和影响,需要进行一定的 trade-off。
Round 操作 实现数据的离散化,将原始连续空间的数值映射到距离它数值最近的离散点。原始数据 x 和其映射后所对应的离散值 x^{\prime} 之间的差值 \Delta x_r = x - x^{\prime} 即为 Round 操作引入的量化误差。我们可以将误差项近似看做服从均值为 0 的正态分布,则有:
\Delta x_r \sim U(-\frac{\beta_x - \alpha_x}{2^{N+1}}, \frac{\beta_x - \alpha_x}{2^{N+1}})
对于每一部分的量化误差, 其最大值不会超过两个相邻的量化离散值的间距,根据公式可知离散量化值之间的间距由原始数据的动态表示范围 \beta - \alpha 决定。在 N 固定的情况下,动态表示范围越大,由 Round 操作引发的量化损失也就越大。
Clip 操作 对 [\alpha, \beta] 外的数据进行截取,使得所有的数据都在动态表示范围内。这些超出范围的数据 x 需要截取映射到 \alpha 或者 \beta , 之间的差值即为 Clip 操作引入的量化误差。
\Delta x_c = \frac{1-sgn(x-\alpha)}{2}(\alpha-x) + \frac{1-sgn(\beta-x)}{2}(x-\beta)
我们来看一个服从正态分布的浮点数据进行线性均匀量化的过程示意:
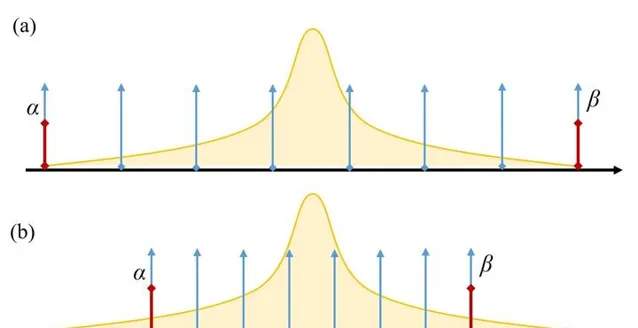
在图3(a) 中,我们选取原始数据的真实最小值和最大值作为动态表示范围 [\alpha, \beta] ,因此不存在超出范围的数值点,即 \Delta x_c = 0 ;因动态表示范围过大,各个离散数据值之间的距离较大,会导致 \Delta x_r 偏大。在图3(b) 中,我们选取了较为合适的动态表示范围来尽可能减小 \Delta x_r ,使得较多的数据分布在 [\alpha, \beta] 外围,这些数据会引入较大的 \Delta x_c ,在长尾分布中引入的误差尤为明显。当前不同的量化算法和优化策略往往是寻找一个恰当的 [\alpha, \beta] ,使得 \Delta x_r+\Delta x_c 较小。
Scaling factor 和动态表示范围在不同的量化方法中有着不同的计算方法,例如在线性均匀量化中,二者之间的关系为:
scale_factor = \frac{2^N - 1}{\beta - \alpha}
通常确定了二者中的一个,另外一个可以根据公式计算得来。除了上述提到的 \Delta x_r 和 \Delta x_c , scaling facor 引入的量化误差主要来源于各个离散数值利用率的平衡性。例如在图3(a) 中,动态范围选取较大带来的另外一个弊端,即为离散数值利用率不均衡的问题。对于 N-bit 的量化,离散数值共有 2^N 种选择(在部分量化策略中会强制保留 1-bit 表示数值 0,则离散数值的选择剩余 2^N - 1 种)。神经网络的原始浮点数据通常服从长尾正态分布,大部分的数值分布在均值附近,量化后映射到 0 值附近;小部分数值会分布在远离均值的位置,带有一定信息量无法完全直接舍弃。较大的动态范围使得离散数值之间的间距较大,大部分分布在均值附近的数据只能映射到少量的离散值上,导致 N-bits 的实际表示能力会损失 1 \sim 2 bits 甚至更多。 如何平衡各个离散数值之间的数据分布和利用率,是当前一些量化策略减少量化损失的方向。
3 常见芯片的量化支持
需要进行量化的模型,其部署目标平台多为边缘侧/终端侧,即对模型的大小和运行速度有一定限制和要求的移动端和嵌入式设备。较为常用的典型硬件平台有 NVIDIA Jetson 系列 GPU、Qualcomm Hexagon 系列 DSP、以及新兴的神经网络加速器。在加速器系列中,我们选取寒武纪(Cambricon) 的推理芯片为例,各类硬件平台对量化的支持情况如下表所示:
| 硬件平台 | 后端推理库 | 权值数据量化支持类型 | 是否支持外部参数写入 |
|---|---|---|---|
| NVIDIA Jetson [1] | TensorRT | per-tensor & per-channel | Yes |
| Quanlcomm Hexagon DSP [2] | SNPE | per-tensor | No |
| Cambricon MLU [3] | CNRT | per-tensor & per-channel | Yes |
其中 per-tensor 的量化方法也称 per-layer,指对于给定的网络层的 weight tensor 中的所有数据共享一个量化参数;per-channel 也称 per-axis,指对于给定网络层的 weight tensor,每一个 axis 对应一个 channel,每个 channel 有自己独立的量化参数。通常情况下,per-channel 因为量化的粒度更细致,量化参数的自由度更高,往往更优于 per-tensor 的量化精度。 NVIDIA TensorRT 在对权值(weights) 的量化上支持 per-tensor 和 per-channel 两种方式,采用对称最大值的方法[4];对于激活值(activations) 只支持 per-tensor 的方式,采用 KL-divergence 的方法进行量化;量化参数既支持内部自动生成,也支持外部指定,支持 weights 和 activations 采用不同的指定方式。更为详细的机制解析和使用方式已有官方技术文档[5]和很多文章[6]进行了分析讲解,感兴趣的同学可以自行阅读,此处不再赘述。 Quanlcomm Hexagon DSP 的官方后端推理库 SNPE 只支持 per-tensor 的量化方式,采用非对称最大最小值的方法[7],并提供 Enhanced Quantization Mode 进行精度优化,暂不支持外部量化参数写入。为了补偿SNPE在使用时的量化精度损失,Quanlcomm 推出了自己的模型量化压缩工具 AIMET[8],支持 DFQ[9]、AdaRound[10]等量化算法,依托于 AIMET 也可以实现部分外部量化参数的写入。通过对AIMET源码的阅读,我们也可以获得如何把量化参数写入SNPE后端的方法。寒武纪 MLU 系列加速器的官方后端为 CNRT,同样支持 per-tensor 和 per-channel 两种量化方法,也支持外部参数的写入,但只支持 weights 和 activations 采用同样的指定方式,即同时由内部生成或同时由外部指定。我们可以看到,当前的硬件平台除了自身的工具链提供的原生量化方法外,大部分均支持外部参数的写入,通过指定 scaling_factor 或动态范围 [\alpha, \beta] 二者之一,另外一个在内部通过计算得到。当原生量化工具无法满足模型部署精度需求时,我们可以通过误差分析,自行调整量化参数,从而达到恢复精度的目的。
4 结语
本文对量化过程中的误差来源进行了粗略的归类,理解这些误差如何在计算过程中引入,并对各个误差项之间的耦合和影响关系进行了分析。当前很多量化算法和优化策略本质上还是在寻找一些减小这些误差项的方法,并在其中寻找平衡点。例如,AdaRound 算法不再采用四舍五入的方法,而是采用一种自使用的策略动态决定向上取整还是向下取整,从而减小 Round 操作引入的误差项 \Delta x_r ;DFQ 算法通过计算恒等性修改权值数据的分布,减少长尾部分的数据,从而减少Clip操作引入的误差项 \Delta x_c ,同时也可以有效降低 \Delta x_r 和离散值利用率低的问题;ACIQ[11] 算法直接通过对优化问题求解,得到最优的动态范围,从而降低上述误差项,等等。本文对量化误差背后的基本原理进行了介绍,关于如何评估哪类误差对整个网络最终的结果起到了更大的影响,如何根据损失去选择合适的量化算法等问题,欢迎持续关注 AI 框架技术分享模型部署专题系列。
PS:欢迎大家关注 AI 框架技术分享专栏内容,如果有感兴趣的技术内容和难点欢迎随时指出,可以多多评论留言。我们也希望能通过本次技术分享让大家了解到更多的 AI 框架前沿技术,也期待和大家一起探讨,更欢迎大家加入我们,一同为 AI 框架及 AI 发展贡献力量!简历直投邮箱:[email protected]
参考文献
[1] NV TensorRT官方文档 https:// docs.nvidia.com/deeplea rning/tensorrt/developer-guide/index.html
[2] SNPE官方文档 https:// developer.qualcomm.com/ docs/snpe/model_conversion.html
[3] 寒武纪MLU290用户手册 https:// usermanual.wiki/Cambric on-Technologies/MLU290
[4] NV 2017-05-06 Presentation Slices https://www. slideshare.net/cfregly/ advanced-spark-and-tensorflow-meetup-20170506-reduced-precision-fp16-int8-inference-on-convolutional-neural-networks-with-tensorrt-and-nvidia-pascal-from-chris-gottbrath-nvidia
[5] 8-bit-inference-with-tensorrt Slices https:// on-demand.gputechconf.com /gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf
[6] Int8量化-介绍(一) https:// zhuanlan.zhihu.com/p/58 182172
[7] SNPE量化说明 https:// developer.qualcomm.com/ docs/snpe/quantized_models.html
[8] AIMET https:// github.com/quic/aimet
[9] Data-Free Quantization Through Weight Equalization and Bias Correction https:// arxiv.org/abs/1906.0472 1
[10] Up or Down? Adaptive Rounding for Post-Training Quantization https:// arxiv.org/abs/2004.1056 8
[11] Post-training 4-bit quantization of convolution networks for rapid-deployment https:// arxiv.org/abs/1810.0572 3










