這道題這麽多人問呀, 第四次回答. 一般就是按照機械能守恒判斷呀, 系統機械能守恒, 但顯然兩球各自的機械能不守恒, 各自機械能的變化量大小相等, 一正一負, 相互抵消, 所以桿對兩個小球都是做功的, 只是一個做正功, 一個做負功, 做功大小相等, 但一正一負, 在系統裏相互抵消. 以下具體分析:
自由轉動的桿中,如果桿連線著兩個或以上的品質不可忽略的物體時,那麽在研究其中一個物體的受力時,自由轉動的桿就不能看作輕質的二力桿模型,應看作有重力作用的桿,此種情況桿不僅會產生拉伸形變,也會發生彎曲形變,桿對物體的彈力就不沿桿的方向.
此題容易錯誤認為兩個小球在轉動過程中機械能守恒, 而事實上若研究其中一個球時,桿就不能看作自由轉動的輕桿,桿會發生微小彎曲形變,對物體的彈力不沿桿的方向,桿對 A
球或 B
球均有做功, 並使 A
或 B
機械能不守恒, 但是 A,B
組成的系統與外界沒有能量交換,系統機械能還是守恒的。
所以本題中桿對 A,B
兩球均有做功,且桿對兩球總功為零,系統只有重力做功 ,系統機械能守恒. 以下定量分析.
剛性連線體做定軸轉動時, 與角相關的量(角位移 \theta
, 角速度 \omega
, 角加速度 \varepsilon
)相同. 設系統下降過程中與豎直方向的夾角為 \theta
, 每桿長 r
, 兩小球品質均為 m
, 則在下降過程中兩球速度之比 {v}_{{B}}=2{v}_{{A}}
, 由系統機械能守恒可得: \begin{equation}{m}{g}{r}{\operatorname{cos}{\theta}}+{m}{g}.2{r}{\operatorname{cos}{\theta}}={\frac{1}{2}}{m}{{v}_{{A}}^{2}}+{\frac{1}{2}}{m}{{v}_{{B}}^{2}}={\frac{1}{2}}{m}{{v}_{{A}}^{2}}+{\frac{1}{2}}{m}{{\left(2{v}_{{A}} \right)}^{2}} \\ 3{m}{g}{r}{\operatorname{cos}{\theta}}={\frac{5}{2}}{m}{{v}_{{A}}^{2}}\Rightarrow{v}_{{A}}={\sqrt{{\frac{6}{5}}{g}{r}{\operatorname{cos}{\theta}}}};~{v}_{{B}}=2{v}_{{A}}={\sqrt{{\frac{24}{5}}{g}{r}{\operatorname{cos}{\theta}}}}\end{equation}
A,B
小球對 O
點的轉動慣量分別為 mr^2,m(2r)^2=4mr^2;
按照系統轉動慣量的組合定理, 系統的轉動慣量 \begin{equation}{J}={m}{r}^{2}+4{m}{r}^{2}=5{m}{r}^{2}\end{equation}
;
淨外力矩 \Sigma{M}_{{O}}={m}{g}{r}{\operatorname{sin}{\theta}}+{m}{g}.2{r}{\operatorname{sin}{\theta}}=3{m}{g}{r}{\operatorname{sin}{\theta}}
;
由剛體轉動定律 \Sigma{M}_{{O}}={J}\epsilon
得轉動的角加速度 \begin{equation}\epsilon={\frac{{M}_{{O}}}{{J}}}={\frac{3{m}{g}{r}{\operatorname{sin}{\theta}}}{5{m}{r}^{2}}}={\frac{3{g}}{5{r}}}{\operatorname{sin}{\theta}}\end{equation}
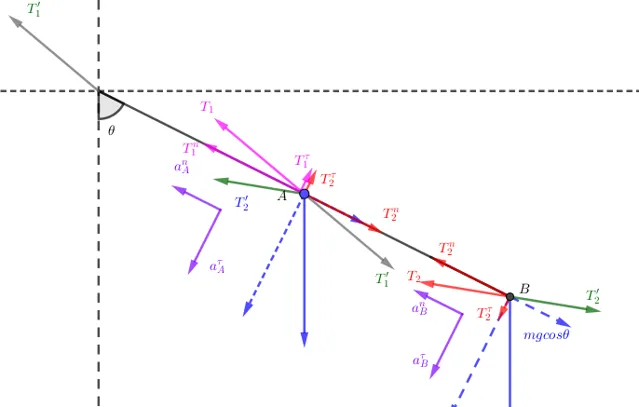
按照切向加速度 a^\tau
和法向加速度 a^n
對 A,B
作運動分析, 定軸轉動沿徑向速度不變, 法向加速度就是向心加速度只改變速度方向, 切向加速度等於角加速度乘以轉動半徑(或者曲率半徑), 受力分析按照法向和切向分別分析, 兩個方向的分力除重力的分力提供外, 由兩桿提供另兩個分力. 所以 \begin{equation}{\left \{ ~\begin{matrix}{{a}^{{n}}_{{A}}={\frac{{v}_{{A}}^{2}}{{r}}}={\frac{6}{5}}{g}{\operatorname{cos}{\theta}};~{a}^{{n}}_{{B}}={\frac{{v}_{{B}}^{2}}{2{r}}}={\frac{12}{5}}{g}{\operatorname{cos}{\theta}}}\\ {a}^{\tau}_{{A}}={r}\epsilon={\frac{3}{5}}{g}{\operatorname{sin}{\theta}};~{a}^{\tau}_{{B}}=2{r}\epsilon={\frac{6}{5}}{g}{\operatorname{sin}{\theta}}\ \end{matrix}\right.} \\ \text{ }\end{equation}
如果把兩球和桿 2
組成的系統當做一個整體, 分析桿 1
對其作用力,按照法向和切向分別分析: \Sigma{F}^{{n}}={T}^{{n}}_{1}-2{m}{g}{\operatorname{cos}{\theta}}={m}{a}^{{n}}_{{A}}+{m}{a}^{{n}}_{{B}}={\frac{18}{5}}{m}{g}{\operatorname{cos}{\theta}}\Rightarrow{T}^{{n}}_{1}={\frac{28}{5}}{m}{g}{\operatorname{cos}{\theta}};~ \\ \Sigma{F}^{\tau}=2{m}{g}{\operatorname{sin}{\theta}}-{T}^{\tau}_{1}={m}{a}^{\tau}_{{A}}+{m}{a}^{\tau}_{{B}}={\frac{9}{5}}{m}{g}{\operatorname{sin}{\theta}}\Rightarrow{T}^{\tau}_{1}={\frac{1}{5}}{m}{g}{\operatorname{sin}{\theta}}
桿 1
對球作用力不是沿桿方向的, 因為其在切向也受力. 則桿 1
受到球對其反作用力
{T}'_{1}={\sqrt{{\left({T}^{{n}}_{1} \right)}^{2}+{\left({T}^{\tau}_{1} \right)}^{2}}}={\sqrt{{\left({\frac{28}{5}}{m}{g}{\operatorname{cos}{\theta}} \right)}^{2}+{\left({\frac{1}{5}}{m}{g}{\operatorname{sin}{\theta}} \right)}^{2}}}={\frac{{m}{g}}{5}}{\sqrt{783{\operatorname{cos}^{2}{\theta}}+1}}
也就是沿徑向向外偏下一點兒. 同時轉動軸 O
對桿 1
的作用力與 T'_1
大小相等方向相反.
分析桿 2
的受力情況主要分析其對 B
球的作用力. \begin{equation}{\left \{ ~~\begin{matrix}{{a}^{{n}}_{{B}}={\frac{{v}_{{B}}^{2}}{2{r}}}={\frac{{\left({\sqrt{{\frac{24}{5}}{g}{r}{\operatorname{cos}{\theta}}}} \right)}^{2}}{2{r}}}={\frac{12}{5}}{g}{\operatorname{cos}{\theta}}}\\ {{a}^{\tau}_{{B}}=2{r}\epsilon=2{r}.{\frac{3{g}}{5{r}}}{\operatorname{sin}{\theta}}={\frac{6}{5}}{g}{\operatorname{sin}{\theta}}} \end{matrix}\right.};~ \\ {\left \{ ~\begin{matrix}{\Sigma{F}^{{n}}_{{B}}={m}{a}^{{n}}_{{B}}\Rightarrow{T}^{{n}}_{2}-{m}{g}{\operatorname{cos}{\theta}}={m}.{\frac{12}{5}}{g}{\operatorname{cos}{\theta}}\Rightarrow{T}^{{n}}_{2}={\frac{17}{5}}{m}{g}{\operatorname{cos}{\theta}}}\\ {\Sigma{F}^{\tau}_{{B}}={m}{a}^{\tau}_{{B}}\Rightarrow{m}{g}{\operatorname{sin}{\theta}}+{T}^{\tau}_{2}={m}.{\frac{6}{5}}{g}{\operatorname{sin}{\theta}}\Rightarrow{T}^{\tau}_{2}={\frac{1}{5}}{m}{g}{\operatorname{sin}{\theta}}} \end{matrix}\right.}\end{equation}
桿 2
對 B
的作用力的合力 \begin{equation}{T}_{2}={\sqrt{{\left({T}^{{n}}_{2} \right)}^{2}+{\left({T}^{\tau}_{2} \right)}^{2}}}={\sqrt{{\left({\frac{17}{5}}{m}{g}{\operatorname{cos}{\theta}} \right)}^{2}+{\left({\frac{1}{5}}{m}{g}{\operatorname{sin}{\theta}} \right)}^{2}}}={\frac{{m}{g}}{5}}{\sqrt{289{\operatorname{cos}^{2}{\theta}}+{\operatorname{sin}^{2}{\theta}}}}={\frac{{m}{g}}{5}}{\sqrt{288{\operatorname{cos}^{2}{\theta}}+1}}~\end{equation}
所以桿 2
受到 B
球對其的彈力 T'_{2}
與其對 B
的作用力大小相等, 方向相反, 就是沿徑向向外朝下偏一點. 同樣, 桿 2
在 A
端也是受到大小相等, 方向相反的作用力.
桿對小球的切向反力對小球做功, A
球受到的反力為 {T}^{\tau}_{1}+{T}^{\tau}_{2}={\frac{1}{5}}{m}{gsin\theta}+{\frac{1}{5}}{m}{gsin\theta}={\frac{2}{5}}{m}{gsin\theta}
方向始終與 A
球運動方向即速度方向相反, 所以桿對小球 A
做負功, B
球受到桿的切向反力 {T}^{\tau}_{2}={\frac{1}{5}}{m}{g}{\operatorname{sin}{\theta}}
, 對 B
球做正功, 所以 A
球受到的切向反力是 B
球的兩倍, B
球沿反力方向運動的弧長是 A
球的兩倍, 所以桿對兩球做的功大小相等, 一正一負, 正好相互抵消, 整體機械能守恒. 具體做功數值: \begin{equation}{W}_{{A}}=\int_{{{\frac{\pi}{2}}}} ^{{0}} \overset{\rightarrow}{F}.{d}\overset{\rightarrow}{s}=\int_{{{\frac{\pi}{2}}}} ^{{0}} -{\frac{2}{5}}{m}{g}{\operatorname{cos}{\theta}}.{r}{d}\theta={\frac{2}{5}}{m}{g}{r}{\operatorname{sin}{\theta}}\begin{matrix}{0}\\ \frac{\pi}{2}\ \end{matrix}=-{\frac{2}{5}}{m}{g}{r};~ \\ {W}_{{B}}=\int_{{{\frac{\pi}{2}}}} ^{{0}} \overset{\rightarrow}{F}.{d}\overset{\rightarrow}{s}=\int_{{{\frac{\pi}{2}}}} ^{{0}} {\frac{1}{5}}{m}{g}{\operatorname{cos}{\theta}}.2{r}{d}\theta=-{\frac{2}{5}}{m}{g}{r}{\operatorname{sin}{\theta}}\begin{matrix}{0}\\ \frac{\pi}{2}\ \end{matrix}={\frac{2}{5}}{m}{g}{r};~\end{equation}
這個與水平位置降到豎直位置兩球各自機械能的變化一致. 因為設到最低點 A
球速度為 v
, 則 B
的速度 2v
, 於是系統機械能守恒 \begin{equation}{\frac{1}{2}}{m}{v}^{2}+{\frac{1}{2}}{m}{{\left(2{v} \right)}^{2}}={m}{g}{r}+{m}{g}.2{r}\Rightarrow{\frac{5}{2}}{m}{v}^{2}={m}{g}.3{r}\Rightarrow{v}={\sqrt{{\frac{6}{5}}{g}{r}}}\end{equation}
;
兩球各自機械能的變化為: \begin{equation}\Delta{E}_{{A}}={\frac{1}{2}}{m}{v}^{2}-{m}{g}{r}={\frac{1}{2}}.{m}.{\frac{6}{5}}{g}{r}-{m}{g}{r}={\frac{3}{5}}{m}{g}{r}-{m}{g}{r}=-{\frac{2}{5}}{m}{g}{r}={W}_{{A}};~ \\ \Delta{E}_{{B}}={\frac{1}{2}}{m}{{\left(2{v} \right)}^{2}}-{m}{g}.2{r}={\frac{1}{2}}{m}.4.{\frac{6}{5}}{g}{r}-2{m}{g}{r}={\frac{12}{5}}{m}{g}{r}-2{m}{g}{r}={\frac{2}{5}}{m}{g}{r}={W}_{{B}}\end{equation}
與按照動力學分析出來的結果一致.