東京奧運會的乒乒球比賽已經接近尾聲,激烈的團體賽即將進行最後的爭奪!(中國隊加油!)

賽場上,運動員們透過不同的發球和接球手法,使得桌球在球拍和球桌上交替發出乒乓之聲,形成了激烈的對抗。那麽,比賽對抗的難度、選手技法的高低是透過什麽表現出來的呢?
答案就是——桌球的前進速度和旋轉強度。
運動員出球速度快,留給對手的反應時間就短,能打得對手措手不及;同時,透過不同速度大小和方向出球,能夠形成不同的落點,逼迫對方頻繁進行前後、左右的移動來應對;為了增加還擊難度,還可以在出球時加上各種旋轉,增大對方回球時的失誤機率。

如果用物理老師的話來講:桌球是在重力場中,球體與空氣、球拍和球桌發生交互作用的六自由度運動,包括三個平動和三個轉動自由度。其中, 桌球和球拍的交互作用是關鍵 (嘭嘭嘭,老師敲黑板了!)。
那麽 ,高手打的球為什麽能拐彎?桌球是如何轉起來的?
桌球的旋轉奧秘——靜摩擦
球拍與桌球在碰撞過程中,除了發生正碰外(法向的撞擊力過球心),球拍相對於桌球的切向揮動還會引發相互摩擦力,並使球體發生轉動。故球拍傳遞給球的力是撞擊力與摩擦力的合力,前者改變球體的速度方向和大小,後者改變球體的轉動方向和大小。
如果沒有摩擦力,就不能發生旋轉,這也是「光板」球拍時代打不出像樣旋轉球的原因。
從二十世紀五十年代開始,能產生摩擦力的 反貼膠球拍 出現,亞洲選手的「弧圈球」一舉橫掃歐洲,令世界桌壇「談弧色變」。
1981年第36屆世桌賽上,中國選手蔡振華在決勝局緊要關頭,以不同旋轉發球的技法連得5分,戰勝蓋爾蓋伊。
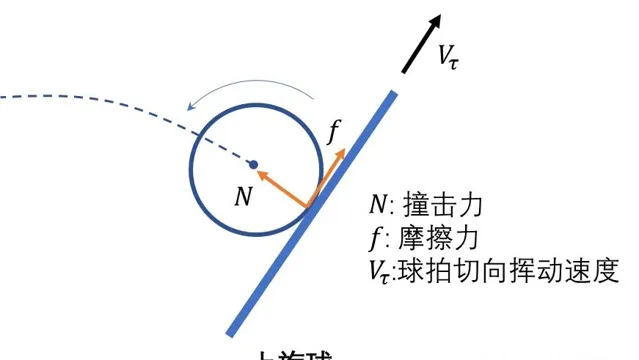
而為了達到可控的旋轉,就要避免在球拍和桌球碰撞過程中出現滑動摩擦,讓整個過程處於靜摩擦力的作用範疇,也就是要使桌球旋轉起來的切向速度與球拍的切向揮動速度一致。
靜摩擦力與兩個因素有關,一個是撞擊力的大小,一個是球拍「黏性」的大小(就是摩擦力系數啦)。
因此,使得旋轉可控的途徑就有兩個:第一,增大擊球時的出球速度,揮拍越快,拍與球之間的摩擦力越大;第二,提高球拍的「科技」含量,比如利用反貼膠材質和正膠顆粒頂端的細小花紋,或刷膠灌油等技術提高球拍的「黏性」。
如今,花樣百出的旋轉已經成為賽場上的基本「殺傷」手段。
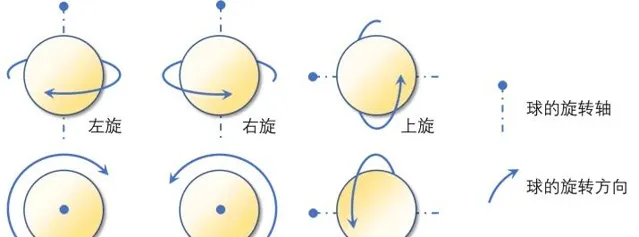
桌球的旋轉通常分為六大類:上旋球、下旋球、左旋球、右旋球、順旋球和逆旋球。
當桌球體遠離擊球者時,後半部份向上旋轉為上旋球,向下為下旋球;向左為左側旋球,向右為右側旋球;順時針旋轉為順旋球,逆時針為逆旋球。正常比賽中桌球的旋轉大多是兩個旋轉結合的,比如左上旋球。
除了怎麽轉起來的,再附贈一個怎麽拐彎的回答……那些「反直覺」的弧圈球是怎麽打出來的?
那麽,桌球的旋轉是如何帶來「殺傷」力的呢?是什麽令旋轉的桌球如此「不可捉摸」?
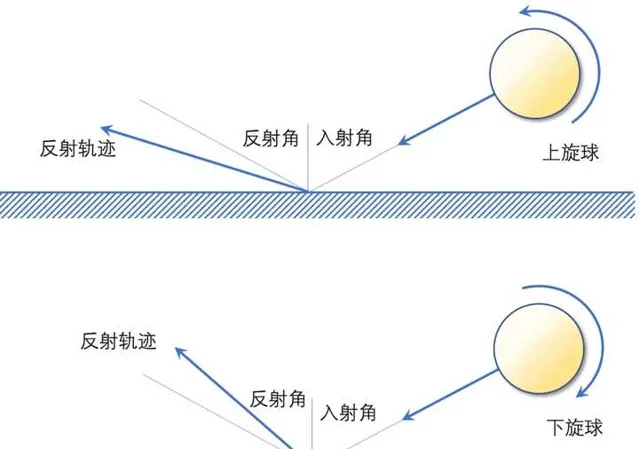
當一個旋轉球與桌面或球拍發生碰撞時,除了撞擊力外還會有摩擦力。在與桌面的碰撞時,如果沒有旋轉,桌球會在撞擊力作用下反彈,摩擦力幾乎可以忽略,反射角基本與入射角相等。 如果桌球有旋轉,那它與桌面碰撞時的摩擦力會使得反射角發生改變。
比如,上旋球與桌面碰撞時,將產生前進方向的摩擦力,使得球體彈起時向前猛沖,反射角大於入射角;下旋球則相反,受到向後的摩擦力,使得反射角小於入射角,甚至可能在前進速度不大而下旋極強時,產生「回跳」現象。
當接球者的球拍和上旋球接觸時,摩擦力會使球沿著拍面「上爬」而增大反彈角度;下旋球則沿著拍面「下鉆」而減小反彈角度。 這就是回擊上旋球時經常出現「遠走高飛」,應付下旋球時容易「自投羅網」的道理。
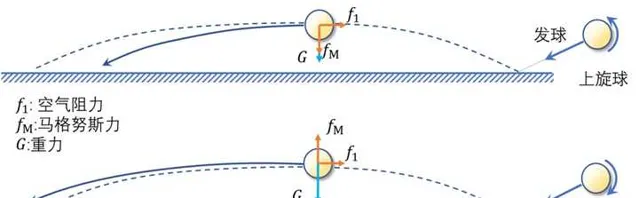
旋轉的桌球不僅在落台和觸拍時會讓人感到「反直覺」,它在空中飛行的路徑也會同樣「反直覺」。 顯然,空中飛行的桌球路徑的改變是與空氣的黏性有關的,這就需要咱們請出空氣動力學來解釋了。
一方面,空氣的黏性使得桌球飛行受阻,前進速度越快,空氣阻力越大。粗略地估算,阻力與速度的平方成正比,這使得桌球的飛行並非拋物線軌跡。
另一方面,旋轉的桌球還會帶動周圍空氣旋轉,使得一側空氣速度增加,另一側速度減小,形成非對稱的氣流。
如果旋轉角速度方向與前進方向不重合(嘭嘭嘭,老師又敲黑板了!),桌球將受到一個「既垂直旋轉角速度方向,又垂直於前進方向」的橫向力,使飛行弧線發生偏移。若是上旋球,則產生向下的力,使得飛行弧線變低;反之,下旋球的飛行弧線升高;而側旋球則朝左右方向飄飛。
在流體力學中,旋轉物體運動產生的橫向力被稱為馬格努斯力(Magnus Force),而這一現象則被稱為馬格努斯效應[1]。 由於空氣阻力和馬格努斯力的存在,飛行速度的大小和方向發生會發生「反直覺」般的非線性改變,這也是傳說中「弧圈球」的來由。
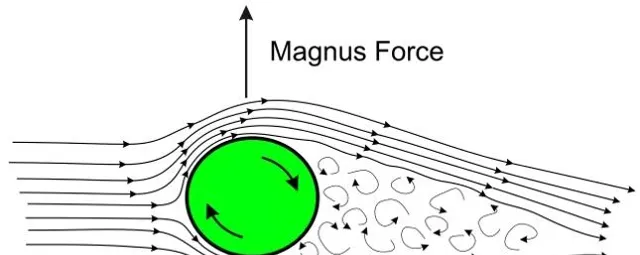
馬格努斯效應不僅為「乒乓必殺技」提供了方法論,更在網球、棒球、排球、籃球等中都有套用,足球計畫中著名的「香蕉球」也是這個原理。
另外,馬格努斯效應還對旋轉炮彈、飛彈的設計和制導控制等有重要意義。
當我們熟悉了這些力學常識後,就能更加「胸有成竹」地與旋轉球周旋,感受桌球比賽優美而錯落的節奏感,欣賞桌球「反直覺」帶來的「確定性」。
參考資料
[1]Kármán, Theodore von (1963): Aerodynamics: McGraw-Hill Education.
[2]https:// funsizephysics.com/spin s-and-skyrmions/
作者:余永亮(中國科學院大學)
出品:科學大院
轉載請聯系[email protected]
後記: 這篇文章釋出2小時後,余老師就被拉進了力學所的乒協群,並收到了戰書: