謝謝知乎的邀請。先簡單回答幾個答主的問題。
關於論文裏很多參數都是取 \log D 的固定冪次,是不是為了湊2022這個數的問題,從Landau-Siegel零點本身來講應該是 \log D 的一個冪次,而他們猜想的實際上應該是負一次方,我這個方法應該能得到負幾百,這個數倒不是故意湊的,但是到底幾百的多少,我也沒有仔細算,我能夠保證的是2022正好差不多到這兒就可以了,正好今年是2022,我順便定在這兒。經常有人幹這種事情,所以這也沒有什麽特別含義,就像之前的7000萬也是。
定理1的2022變小肯定是可以的,但是L函式導數在s=1附近的階,目前只有平凡估計。比如說 L'(s,\chi)\ll(\log D)^2 ,這個二次方目前沒有辦法改進,只能用這個平凡的界。不過這個對我們整個論證過程來講,影響不是太大。
有人問到我論文中參照1975年Goldfeld用復變積分法得到的結果:如果Landau-Siegel猜想成立則可以推出 L(1,\chi)\gg(\log D)^{-1} ,即負一次方的下界。但如果用這個下界反推,只能給出 \log D 負三次方的非零區域。
是這樣,一個方向能夠到負一次方,另一個方向如果直接這麽弄的話顯得有些別扭。目前來看確實是這種情況,兩邊顯得好像不太對稱。如果就零點和 L(1,\chi) 下界之間的關系做一個更新穎的探索,這是完全有可能的,這方面完全可以有一些新的東西。
關於我的論文裏證明了一系列的L函式在一個離實數軸較遠的區域 \Omega 裏的零點都落在臨界線(即實部為1/2的豎線)上。在知乎上,有人問到這部份的方法有沒有可能被用來研究L函式在 \Omega 區域之外的零點分布。
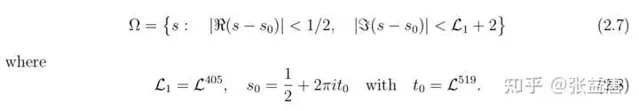
他可能覺得我這部份寫得比較亂。我的 t_0 是 \log D 的519次方。嚴格講如果和D相比的話,它不算大。但是我要取成這樣,比 \log D 大一點,比實數軸高出一截。因為一到實數軸上我用的L函式漸近公式就會顯得很亂,因為Gamma因子包含在函式方程式中,當然s在實數軸上還可能會出現奇異點等麻煩,所以我透過這種辦法將問題避開了。
我做的大部份都是技術性的。為什麽非要這麽取?換一種方法取可不可以?也是完全可能的。但是你做的時候就知道只能取一個,而且希望能取一個相對簡單、清楚的,至於目前的取法是否是最簡單、最清楚的我也不敢說。
還有一個關於等差數列的問題,提到 Bombieri-Vinogradov定理的證明,D較小的時候是用Siegel-Walfisz定理處理,而D較大時用大篩法不等式做。知乎上還有人問如果把我的新誤差代入進去,會不會把Bombieri-Vinogradov中的1/2冪次改良?
直接來講不能改良1/2,但能把誤差上界改進。Bombieri-Vinogradov定理中的誤差上界是 x/(\log x)^A 的形式。你們仔細看證明過程,其實關鍵的部份就是對D較小時的處理。那部份的誤差項只能一個一個做、一個一個去估計。這裏最大的一個障礙還是Siegel零點的問題,這導致大O上界中的常數是不能被有效計算出來的。而現在,我這個東西把這兩個突破了。第一,定理裏頭D的範圍不再是 x^{1/2}/(\log x)^A 的形式了,這個範圍應該是可以算出來的。第二,誤差上界中的常數可以被有效計算出來了。在Bombieri-Vinogradov定理的證明裏,盡管有各種各樣的證明,它最後都是歸結到原特征的時候,對D較大的情況,用大篩法不等式去做,出來的實際上 x^{1-\delta} 形式的項。反而在D比較小時,Siegel零點的存在性就會讓誤差項差這麽一點。肯定誰也不喜歡用Siegel-Walfisz的方法去處理,但是沒有辦法。
很多人對我的經歷很感興趣,覺得我花了這麽多年研究非常困難的數學問題,有沒有想過放棄,是怎麽堅持下來的。我也想借此機會和大家聊聊。
關於Landau-Siegel猜想,我沒有想過放棄,因為這些年我的整個思考也是斷斷續續的。2007年我發過一篇關於Landau-Siegel的論文,其實當時是有可能繼續做下去的,但是後來遇到了一個情況,就是孿生質數的問題一下變得熱門了,所以2010年到2013年去做孿生質數去了,就做出來一個7000萬的結果。後來想想,覺得Landau-Siegel還得做,所以就又回到這個問題上。我一般是幾個問題同時在想,一段時間註重這個,一段時間註重那個,Landau-Siegel實際上上世紀末我就開始想了,我喜歡幾個問題一起想,有一個問題初步想出來了,其他那些就接著想,都是比較大的問題。
前幾天論文公開後,我給北大做了一場遠端講座。我在北大讀研時的導師潘承彪評價:今天聽了益唐講的想法很清楚,這是一個重要的篩法新思想,有很大發展潛力,可實作起來很難。
我當即回復:聽了潘老師的肯定,比聽一萬個人的贊揚更有價值。
今天,我又和知乎上一個關註我論文的小夥子交流,了解到他在倫敦讀大一,學數學。我覺得他是非常不容易的,因為他大一已經能夠學到我在研究生時候學的課程,說明他進步很快,付出了很多,確實是非常聰明的一個小夥子。希望像他一樣的年輕人能發揮自己的想象力,不要把前人的東西看成至高無上的。這個東西別人這麽做的我能不能換一種做法,或者我能不能突破它?不斷自我提問,不斷自我嘗試,走出新的路子來,你們這些年輕人的前程是非常遠大的。
關於我的未來,這些數學問題我是不會丟掉的。我覺得我大概這一輩子就是做數學的命了,我不做數學都不知道幹什麽。別人談過有沒有退休的問題,我說如果我真的離開數學了,我確實不知道我該怎麽活。

平時在家裏,我夫人總是覺得我一個人不太說話,吃完飯自己在房間裏一待,耳機一掛自己聽音樂,玩自己的。她怕我這樣慢慢會神經,還開玩笑說,我老了要是神經了,她可受罪了,還得給我推輪椅。所以她每天把菜切好讓我回家以後學炒菜,不管炒成什麽樣也要炒。周末有時候也找幾個做數學的同事來家裏坐坐,喝酒聊天,但他們說我聊著聊著眼光不對,就走神了。夫人經常批評我這樣不禮貌,說我這樣將來就沒有朋友了。
我夫人覺得我浪漫的時候不多,就連去維也納聽音樂會都要跑到維也納大學,去找哥德爾的雕像,找了半天也沒找到,直到碰到一個剛下班的教授,告訴我們這裏沒有哥德爾的雕像才走。但是我很感謝她帶我來聽音樂會,因為我喜歡聽交響樂,著名的古典音樂大師我都喜歡,首先是貝多芬,特別愛聽他的第六交響曲。

另外我有點特別的是還喜歡布拉姆斯,其他的像柴可夫斯基,還有蕭邦的鋼琴曲我也特別喜歡,尤其是他的作品53號,降A大調波羅乃茲。
其實我年輕的時候也喜歡那時候的校園歌曲,蘇小明就是我那時候的「偶像」。我同學說我當年在北大宿舍裏,誰提蘇小明不好還跟人翻臉。前一段我和夫人去普林斯頓的時候,住在北大校友吳剛的家裏,他家有卡拉OK,我們還放蘇小明的歌在那兒唱,雖然可能跑調了,因為他們都笑我。
我也很喜歡中國的古典詩詞,其中最欣賞杜甫的詩,比如」劍外忽傳收薊北,初聞涕淚滿衣裳」。還有「卻看妻子愁何在,漫卷詩書喜欲狂。白日放歌須縱酒,青春作伴好還鄉。」杜甫有他自己的奔放,「即從巴峽穿巫峽,便下襄陽向洛陽。」百讀不厭,怎麽品這個味道都覺得特別好。杜甫的詩太多了,「風急天高猿嘯哀,渚清沙白鳥飛回。無邊落木蕭蕭下,不盡長江滾滾來。」還有下面兩句我也特別喜歡,「萬裏悲秋常作客,百年多病獨登台。」對仗對得非常好,而且很自然,流傳了一千多年,讓後人一個字一個字地去品它的味道。
幾年前,有位導演找到我說,想把我的故事拍成電影,就像奈許的【A Beautiful Mind】。我是不希望拍,畢竟網路已經把我說得夠多了,我希望最好不要再給我幹擾。奈許是一個偉大的數學家,他在數學等好幾個領域裏都有獨特的貢獻,這部電影拍得非常好。中文轉譯成「美麗心靈」,我遇到很多年輕的中國留學生,他們都看過。
我現在也會幫我的小孫女講講數學。她上二年級的時候就特別喜歡數學,還報了一個電腦編程班。那個班裏都是高中生,她是最小的,那時候連乘法都不會,後來我幫她補了補。現在9歲了,也一直跟著上到四年級了,學校給她選到數學天才班裏了。她很有天賦,說爺爺我要完成你的心願,替你得菲爾茨獎。其實對這個獎我也沒什麽遺憾,我沒有把這些東西看得太重。
九年前,我第一次存取普林斯頓,有人問我有哪一句詩能概括你當時的心情。我參照了杜甫五首詠懷古跡裏的第一首的最後兩句:「庾信平生最蕭瑟,暮年詩賦動江關」。
今天還是這句。











