奇異值分解（SVD）有哪些很厲害的套用？

這篇打算簡單敘述量子演算法近年的主要進展 (之一), 即量子奇異值變換 (quantum singular value transform) ^[1] . 故事的起點是這麽一件事: 給定某個隨機演算法, 我們總是可以透過多次重復執行它來提高成功機率. 那麽, 我們能盡可能少的重復嗎? 量子演算法中著名的振幅放大 (amplitude amplification) 技術 ^[2] 可以提供平方時間加速, 這裏技術的例子之一就是 Grover 演算法 (或者說"無結構搜尋"演算法).

這個技術做得事情就是在某個 圓周 上做多次 固定角度 逆時針旋轉, 以期在若幹次後到達圓周的頂點. 但這麽做有個問題, 就是如果我們並不知道"固定角度"到底是多少的話, 我們並不能直接透過連續多次旋轉到達頂點附近 – 直到量子奇異值變換 (quantum singular value transform) 相關技術 ^[3] 的出現解決了這一問題, 方案有些出人意料: 只需要 把圓周"撐成"球面 , 然後在上面繞著某兩個軸交替旋轉, 可以證明這樣的旋轉會在球面的極點附近收斂. 這即是不動點振幅放大 (fixed-point amplitude amplification) ^[4] 技術.

為什麽這跟奇異值分解有關呢? 簡而言之, 上面所切換的兩個旋轉軸, 其實跟某個矩陣的奇異值分解 (singular value decomposition) 的左奇異向量及其正交向量張成的平面, 以及右奇異向量及其正交向量張成的平面有關.

本文亦發表於我的部落格: 如何提高成功機率：量子奇異值變換簡說.

下面開始正文.

以平面旋轉來提高成功機率

給定某個成功機率為 p 的隨機演算法, 為了提高它的成功機率 (譬如說成功機率接近 1 ), 我們可以這麽做: 將這個演算法重復允許很多遍, 如果其中有一個拷貝是成功的話, 我們就認為這個新的隨機演算法是成功的. 不難證明, 如果我們重復允許這個演算法, 直到某一次成功才停下來的話 (滿足幾何分布),那麽期望重復次數是 1/p .

我們能在其他模型下做的更好嗎? Gilles Brassard 和 Peter Høyer 在 1997 年證明了 ^[2] , 對於量子演算法, 我們只需要"重復" O(1/\sqrt{p}) 次. 對量子演算法稍有些了解的讀者不難意識到, 著名的 Grover 演算法其實是這一問題的特殊情況 ^[5] , 同樣提供了關於時間復雜度的平方加速. 具體來說, 這一問題可以寫作:

如果取 |\psi_{\rm final}\rangle 為 |\psi_{\rm good}\rangle 的話, 不難發現這個問題有個很漂亮的幾何解釋:

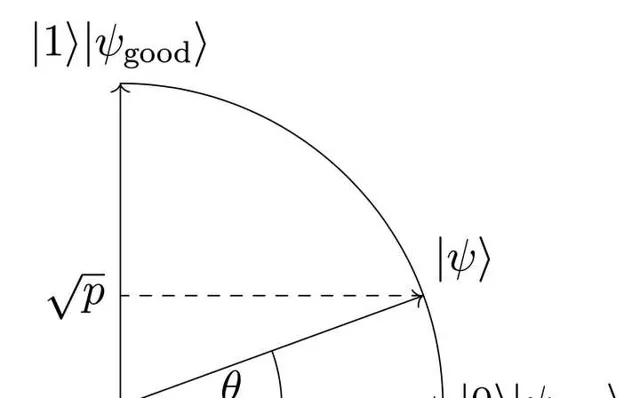
即 |1\rangle|\psi_{\rm good}\rangle 和 |0\rangle|\psi_{\rm bad}\rangle 其實可以張成一個平面上的圓, 它們分別對應於圓上的兩點; 而 |\psi_{\rm init}\rangle 當然也可以投影到這個圓上. 換而言之, 問題變成了, 我們能夠設法使得從圓心指向 |\psi_{\rm init}\rangle 的向量, 能夠繞著圓心旋轉到 |\psi_{\rm final}\rangle ? 這裏的量子演算法 U 其實描述的就是這個旋轉過程 -- 展開來說, 這裏通常包括繞著兩個軸 |0\rangle|\psi_{\rm bad}\rangle 和 U|0\rangle^{\otimes k} 反射, 然後交替這兩個反射過程, 即作用 Grover 算子 G_U=U(2|0\rangle\langle 0|^{\otimes k}-I_k) U^{\dagger}((2|0\rangle\langle0|-I_1)\otimes I_{k-1}) , 就會繞著圓心逆時針旋轉.

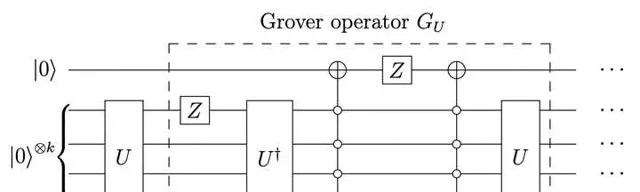
但是上面的旋轉演算法有個問題, 為了計算需要旋轉多少次, 我們需要知道 Grover 算子每次會在這個圓上逆時針旋轉多少度. 但總有些時候我們並不知道旋轉角度, 也就是說, 如果我們 連續地 用 Grover 算子作用在 同一個圓 上 (所謂 fixed-point) 轉的話, 很可能總是會轉過頭的.

於是, 有更好的辦法嗎?

量子奇異值變換和分解定理

上面的振幅放大 (amplitude amplification ) 其實只考慮了二維的希爾伯特空間, 或者說一個量子位元. 令人驚訝的是, 在很多時候其實我們只需要考慮二維空間, 譬如說 Jordan 引理 ^[6] 就告訴我們, 對於兩個投影算子 \Pi_1,\Pi_2 , 他們所作用的希爾伯特空間可以被正交分解成一群一維不變子空間和一群二維不變子空間; 這些不變子空間的維度取決於他們對應的 \Pi_1\Pi_2 的特征值是否為 0 或 1 , 如果都不是的話是二維, 否則是一維.

Jordan 引理可以用來做一些很神奇的事情, 譬如用同一個"證據"態 (witness state) 來做 \mathsf{QMA} 的 error reduction ^[7] , 或者來對量子零知識證明來做 rewinding ^[8] . 是的, 這些套用聽起來很反直覺, 因為把量子路線作用到量子態後, 再做測量通常會把量子態弄得面目全非; 但這裏的分解定理告訴我們, 在一些情況下, 量子態們只會在二維子空間裏跳來跳去. 這也意味著我們可以設法重復利用這些量子態們.

András Gilyén, Guang Hao Low, 宿願和 Nathan Wiebe 在 2018 年的工作 ^[1] 把上述 Jordan 引理推廣到了更一般的情形, 即

有趣的是, 這裏的不變子空間的維度, 跟它們對應的 \Pi_1 U \Pi_2 的奇異值分解中對應的奇異值是否為 0 或 1 有關: 如果都不是的話, 那麽不變子空間的維度是二維.

展開來說, 考慮 \tilde{\Pi} U \Pi 的奇異值分解, 即 \tilde{\Pi} U \Pi = \sum_{i=1}^{d_{\rm min}} \sigma_i |\tilde{\psi}i\rangle\langle \psi_i| , 其中d_{\rm min}=\min\{d,\tilde{d}\} , 並且 d:={\rm rank}(\Pi) 和 \tilde{d}:={\rm rank}(\tilde{\Pi}) . 對於奇異值滿足 0 < \sigma_i < 1 的情形, 分別可以定義 |\psi_i\rangle 的正交向量 |\psi_i^{\perp}\rangle := \frac{(I-\Pi)U^{\dagger}|\tilde{\psi_i}\rangle}{\sqrt{1-\sigma_i^2}} , 以及 |\tilde{\psi}_i\rangle 的正交向量 |\tilde{\psi}_i^{\perp}\rangle:=\frac{(I-\tilde{\Pi})U|\psi_i\rangle}{\sqrt{1-\sigma_i^2}} , 其中奇異值 \sigma_i^2 = \langle \psi_i | U \Pi U^{\dagger} | \tilde{\psi}_i\rangle . 也就是說左奇異向量對應是不變子空間是 \tilde{H}_i:={\rm span}(|\tilde{\psi}_i\rangle,|\tilde{\psi}_i^{\perp}\rangle) , 右奇異矢對應的不變子空間是 H_i:={\rm span}(|\psi_i\rangle,|\psi_i^{\perp}\rangle) ; 而 U 則是從 H_i 跳到 \tilde{H}_i , 同時作用旋轉矩陣 R(\sigma_i):=\begin{pmatrix} \sigma_i & \sqrt{1-\sigma_i^2}\\ \sqrt{1-\sigma_i^2} & -\sigma_i \end{pmatrix} .

於是我們可以重新審視上一節中的 Grover 算子 G_U=U(2|0\rangle\langle 0|^{\otimes k}-I_k) U^{\dagger}((2|0\rangle\langle0|-I_1)\otimes I_{k-1}) . 其實它可以被推廣為下述形式: e^{i \phi_1(2\tilde{\Pi}-I)} U \Pi_{j=1}^{(n-1)/2} \left( e^{i \phi_{2j} (2\Pi-I)} U^{\dagger} e^{i\phi_{2j+1}(2\tilde{\Pi}-I)} U \right) , 其中 e^{i\phi_k(2\Pi-I)} 等於先作用 \mathrm{C_{\Pi}NOT} , 然後在控制量子位元上作用 e^{-i\phi_k\sigma_z} , 然後再作用 \rm C_{\Pi}NOT . 註意到 \phi_k=\pi 的時候, 我們有 e^{i \pi \sigma_z}=2|0\rangle\langle 0|-I ; 即旋轉角度 \{\phi_i\}_{i=1}^n 都取 \pi 的時候, 就是振幅放大 (amplitude amplificatio) 演算法. 這意味著我們有一些額外的自由度, 來控制這樣的量子演算法的表現.

現在, 讓我們聚焦到量子奇異值變換中的分解定理匯出的那些二維不變子空間們. 註意到左奇異值向量及其正交向量可以張成一個平面 (右奇異值向量及其正交向量相同), 在這兩個平面上我們同樣可以考慮他們類似振幅放大演算法中的圓; 但是這裏我們可以在在這兩個不同的平面上繞著圓心旋轉 (即作用 2\tilde{\Pi}-I 或 2\Pi-I ), 並且可以透過作用 U 和 U^{\dagger} 來交替切換平面. 那麽有沒有辦法來控制不同的平面的旋轉角度呢? 或者說, 給定一組旋轉角度, 我們能有辦法知道這一系列操作最終做了什麽嗎?

Isaac Chuang 和 Guang Hao Low 更早的工作 ^[3] 給出了二維不變子空間中的答案. 事實上上述操作序列可以看成 量子訊號處理 (quantum signal processing); 換而言之, n 次不同平面上的交替旋轉操作, 相當於對奇異值 \sigma_l 作用了某個 n -次多項式 P , 即 \prod_{j=1}^n e^{i\phi_j \sigma_z} R(\sigma_l) = \begin{pmatrix} P(\sigma_l) & \cdot\\ \cdot & \cdot\ \end{pmatrix} . 更進一步, 借助量子奇異值變換給出的分解定理, 我們可以對所有不變子空間都做類似的操作, 即 f^{(SV)}(\tilde{\Pi} U \Pi)=\sum_{i=1}^{d_{\rm min}} f(\sigma_i) |\tilde{\psi}_i\rangle\langle\psi_i| .

下面我們將給出量子奇異值變換的一個具體套用, 即怎麽解決不動點振幅放大 (fixed-point amplitude amplification) 問題.

以球面旋轉來提高成功機率

回憶一下, 第一節提到的可逆量子演算法 U 的形式是 U:|0\rangle^{\otimes k} \mapsto \sqrt{p}|1\rangle|\psi_{\rm good}\rangle+\sqrt{1-p}|0\rangle|\psi_{\rm bad}\rangle . 換而言之, U 的奇異值分解一定會得到對應於左奇異向量 |\psi_G\rangle:=|1\rangle|\psi_{\rm good}\rangle 和右奇異向量 |\psi_0\rangle:=|0\rangle^{\otimes k} 的奇異值. 此時這一可逆量子演算法的成功機率 p 滿足 \tilde{\Pi} U|\psi_0\rangle=p|\psi_G\rangle , 其中 \tilde{\Pi}:=|1\rangle\langle 1|\otimes I . 也就是說, 為了放大這一可逆量子演算法的成功機率, 我們需要下述奇異向量變換:

對於任務 2, 我們需要某個函式, 使得所有奇異值都能被替換為 1 . 又註意到奇異值變換中的奇異值都是非負的 (因為 A 的奇異值變換是用 A^{\dagger} A 定義的), 看起來 sign 函式正好能滿足我們的需求:

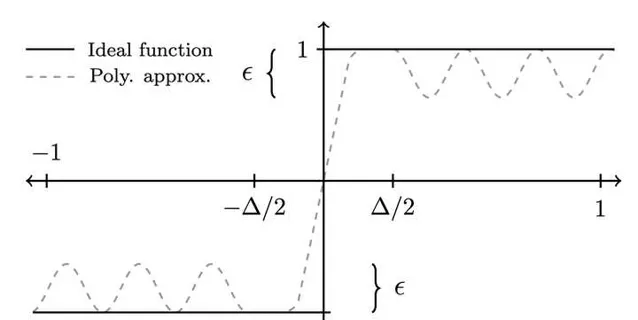
Sign 函式即對於所有大於零的輸入輸出 1, 對於所有小於零的輸入輸出 -1. 而在上一節的討論中, 我們知道每個奇異值變換的一系列旋轉操作最終對應於某個多項式函式. 也就是說, 我們需要做的是找到某個多項式函式, 使得其能夠很好地近似 sign 函式.

幸運的是, 選取合適參數的高斯誤差函式 {\rm erf}(kx):=\frac{2}{\sqrt{\pi}} \int_0^{kx} e^{-t^2} {\rm dt} 就能很好地近似 sign 函式, 而高斯誤差函式亦能很好地用多項式函式近似. 即我們可以找到能在 [-1,1]\setminus (-\delta,\delta) 區間內以 \epsilon 誤差近似 sign 函式的次數為 O(\log(1/\epsilon)/\delta) 的多項式. 這意味著我們可以透過這一具體的多項式, 選擇量子奇異值變換中所需要的一系列旋轉角度. 再註意到 \tilde{\Pi} U \Pi = p|\psi_G\rangle\langle\psi_{\rm init}| , 其中 \Pi=|\psi_{\rm init}\rangle\langle \psi_{\rm init}| , 從而我們給出了任務 2 所需要的構造. 即我們找到了某種基於量子演算法的神奇"重復方式", 使得我們最終得到的結果向量總是很接近目標向量, 不管我們到底重復了多少次.

這樣的做法有什麽幾何解釋嗎? 從上一節中我們知道, 量子奇異值變換可以看成現在某個平面上 (對應於某法向量) 以選定角度旋轉; 再跳轉到另一個平面 (對應於另一個法向量) 上, 以另一個選定角度旋轉; 以此類推. 有趣的是, 在 Isaac Chuang 等人的綜述 ^[9] 中指出下述幾何解釋:

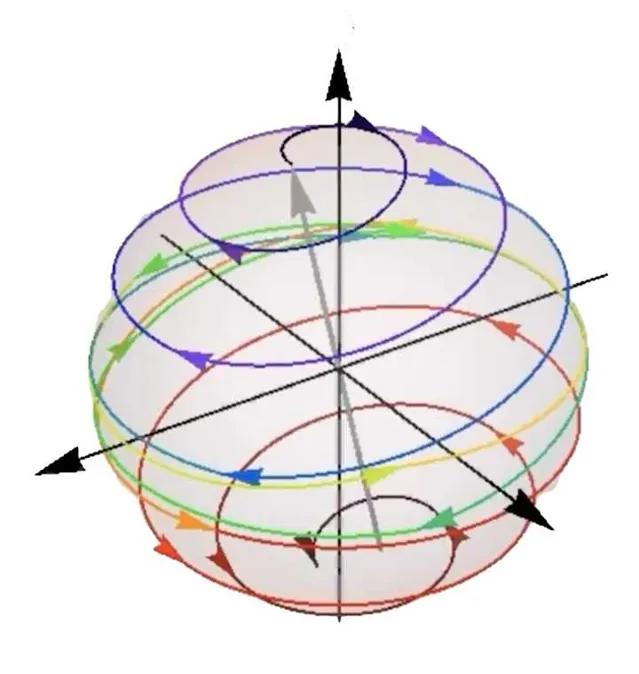
換而言之, 這裏的構造相當於考慮兩頂點分別為 |\psi_B\rangle 和 |\psi_{G}\rangle 的 Bloch 球面, 從頂點 |\psi_{B}\rangle 附近的球面上的點 |\psi_{\rm init}\rangle 出發, 在球面上環繞接近 |\psi_G\rangle , 並最終停留在 |\psi_{G}\rangle 附近. 這也就是為什麽基於量子奇異值變換的構造能避免轉過頭 (即 overshooting) 的直觀原因.

參考

1. ^ ^{a b} Gilyén, András, Yuan Su, Guang Hao Low, and Nathan Wiebe. "Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics." In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, pp. 193-204. 2019.
2. ^ ^{a b} Brassard, Gilles, and Peter Hoyer. "An exact quantum polynomial-time algorithm for Simon's problem." In Proceedings of the Fifth Israeli Symposium on Theory of Computing and Systems, pp. 12-23. IEEE, 1997.
3. ^ ^{a b} Low, Guang Hao, and Isaac L. Chuang. "Optimal Hamiltonian simulation by quantum signal processing." Physical review letters 118, no. 1 (2017): 010501.
4. ^ Yoder, Theodore J., Guang Hao Low, and Isaac L. Chuang. "Fixed-point quantum search with an optimal number of queries." Physical review letters 113, no. 21 (2014): 210501.
5. ^ 準確地說, Grover 演算法給出了 OR 函式的查詢復雜度上界, 而 Brassard 和 Hoyer 的工作則是為了在一些情形下給出精確振幅放大 (exact amplitude amplification).
6. ^ Regev 的講義中有很清晰地表述: Regev, O. "Witness-preserving QMA amplification." Quantum Computation Lecture notes, Spring (2006).
7. ^ Marriott, Chris, and John Watrous. "Quantum arthur–merlin games." computational complexity 14, no. 2 (2005): 122-152.
8. ^ Watrous, John. "Zero-knowledge against quantum attacks." SIAM Journal on Computing 39, no. 1 (2009): 25-58.
9. ^ Martyn, John M., Zane M. Rossi, Andrew K. Tan, and Isaac L. Chuang. "A grand unification of quantum algorithms." arXiv preprint arXiv:2105.02859 (2021).