有一個看似顯而易見,然而兩千年努力發現證明不了的東西: 平行公設
平行公設:若平面內一條直線和另外兩條直線相交,若在直線同側的兩個內角之和小於兩直角,則這兩條直線經無限延長後在這一側一定相交。
按理說公設是無法證明的東西。但和前4個公設相比, 平行公設看起來似乎更像一條定理而不是公設, 人們懷疑它的獨立性,兩千年間,許多數學家投身到證明平行公設的難題之中。
1 歐式幾何五大公設
公設1:任意一點到另外任意一點可以畫直線 公設2:一條有限線段可以繼續延長公設3:以任意點為心及任意的距離可以畫圓公設4:凡直角都彼此相等公設5:同平面內一條直線和另外兩條直線相交,若在某一側的兩個內角和小於二直角的和,則這二直線經無限延長後在這一側相交。經過證明人們知道了, 平行公設等價於三角形內角和等於180度
如果公設1,2,3,4能夠證明公設5,那麽我們就可以在 只使用1,2,3,4的情況下,得到三角形內角和等於180度 。
2 薩開裏試證
2.1 薩開裏四邊形
這是薩開裏定義的一個四邊形,其中 \angle A 和 \angle B 是直角,AC=BD,滿足這些條件的四邊形稱為 薩開裏四邊形
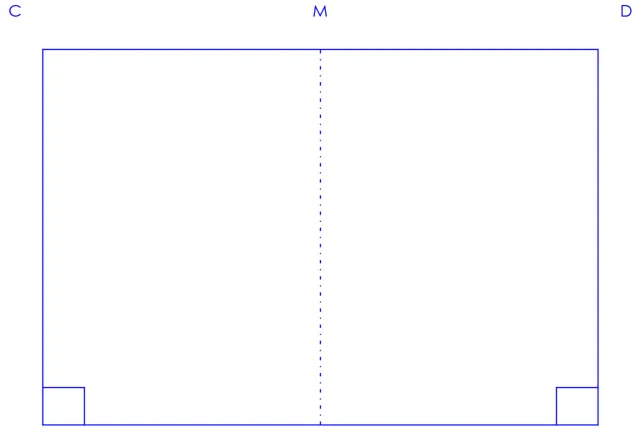
在薩開裏四邊形中,我們可以證明到兩頂角相等( \angle C = \angle D ),兩底邊(AB,CD)的中點連線(MN)是兩底邊的中垂線。
2.2 三種假設
\angle C = \angle D ,薩開裏提出了三種假設:
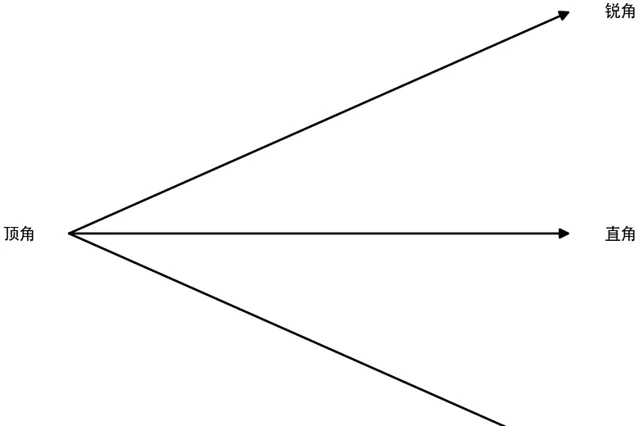
薩開裏證明了在 頂角為直角時,三角形內角和等於180度
只需要再證明出 頂角為鈍角和銳角時會產生矛盾 ,就可以得到結論。
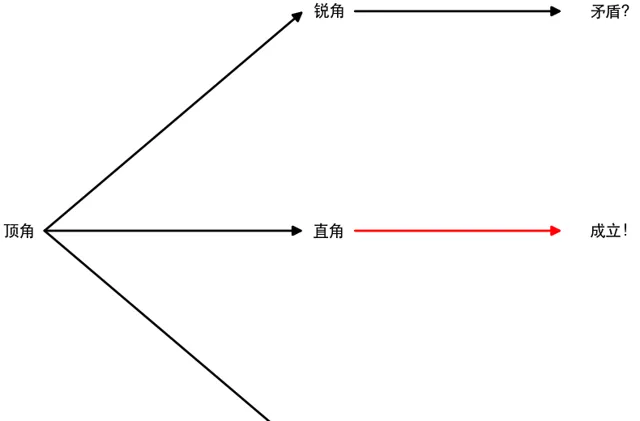
我們先來看看鈍角假設: \angle C 、 \angle D 為鈍角
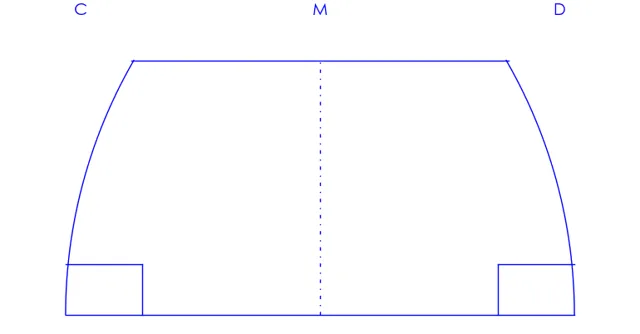
薩開裏證明了它不成立,因為它違反了公設2: 一條有限線段可以繼續延長 。
延長BD
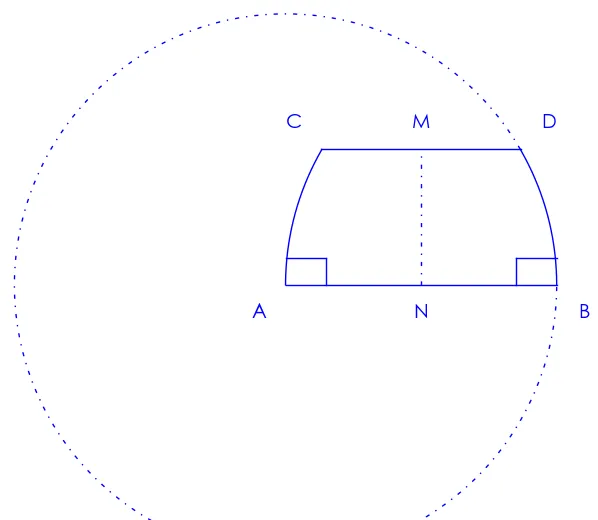
從圖中我們可以看出,延長BD後,BD最終會變成一個封閉的圖形,不能繼續延長。所以它不成立。

銳角假設
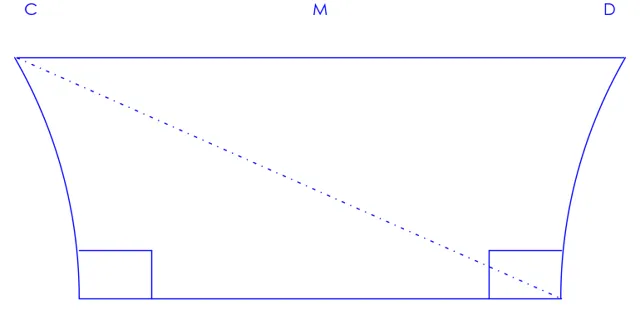
可以得出三角形ABC內角和小於180度(先證明 \angle DBC > \angle ACB 即可)
在銳角假設下,薩開裏在 沒有邏輯矛盾的情況下 ,匯出了很多結論:如三角形內角和小於180度、過直線外一點可以作無數條平行線。但它認為這種現象 違反常理 ,因此認為匯出了矛盾,他認為銳角假設不成立。
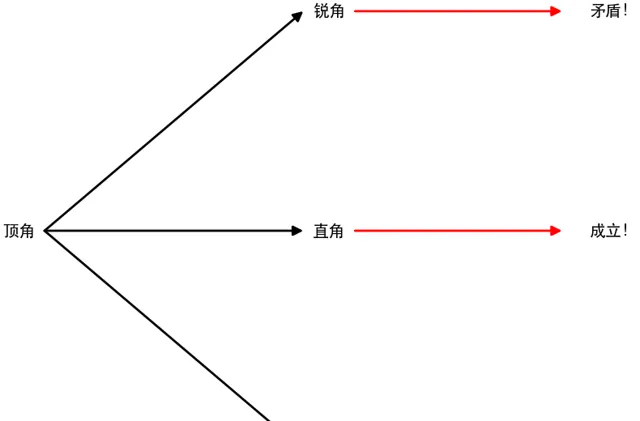
薩開裏推出銳角的情況不成立,直角的情況成立,鈍角的情況不成立,所以他認為他證明了平行公設。
實際上,薩開裏銳角假設下的現象只是和人們的日常觀念相矛盾,並沒有邏輯矛盾,因此薩開裏並沒有證明第五公設。
很可惜,如果薩開裏將銳角假設的研究深入下去,說不定非歐幾何能早誕生100年。
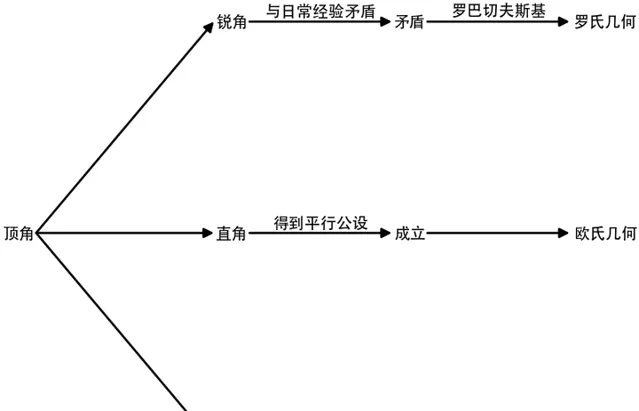
在歐式幾何中,三角形內角和等於180度,在非歐幾何中三角形是怎樣的呢?
3 非歐幾何中的三角形
內角和大於180度的三角形 。
將地球表面看作一個平面,那麽直線是什麽樣子的呢?

可以知道 經線與赤道都是直線
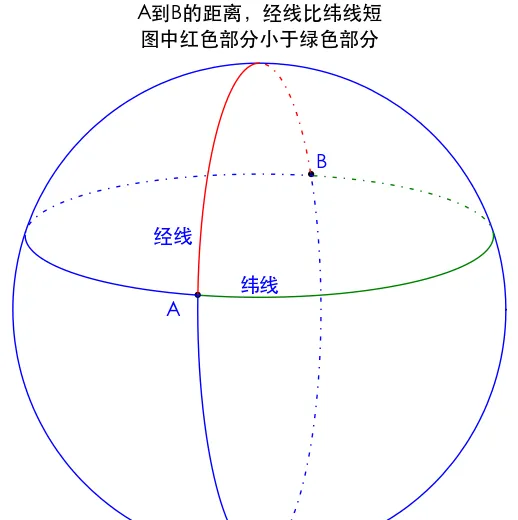
可以看到,這樣的直線也滿足: 兩點距離最短,兩點確定一條直線
以地球的赤道與兩條經線作為邊所形成的三角形,內角和大於180度

黑色的三角形,內角和大於180度
赤道和經線 不能無限延長 。也驗證了薩開裏所說的,鈍角情況下不滿足第二公設。
內角和小於180度的三角形
如果是在一個凹進去的球上,三角形是這樣的
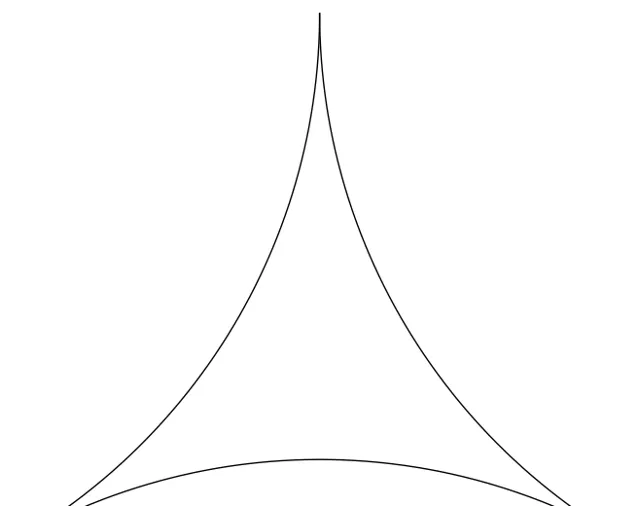
三角形邊越長,內角的和就越小,並且三角形的面積不大於一個定值。
4 非歐幾何中的平行線
4.1 黎曼說:直線沒有平行線
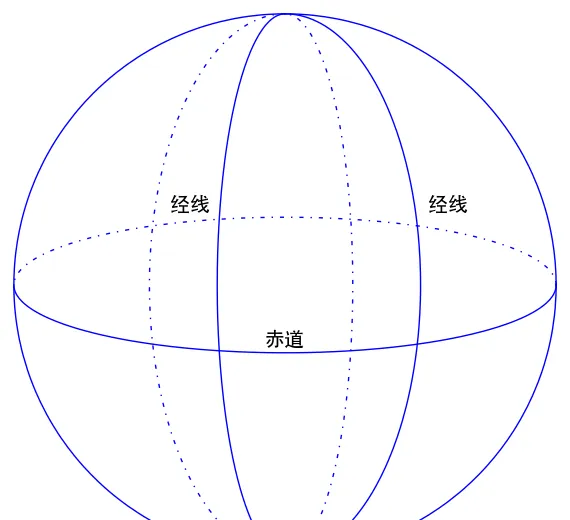
前面提到什麽是球面上的直線,可以知道球面上 所有的直線都相交 。
4.2 羅巴切夫斯基說:直線至少有一條平行線。
龐加萊非歐模型
在平面上作一條直線u,直線將平面分為兩部份,直線上半平面(不包含直線u上的點)為我們所要的非歐平面,記作L。
我們將 圓心在u上的半圓或者垂直於u的射線稱為L直線 。(垂直於u的射線也可看作是圓心在u上,半徑無限大的圓周。)
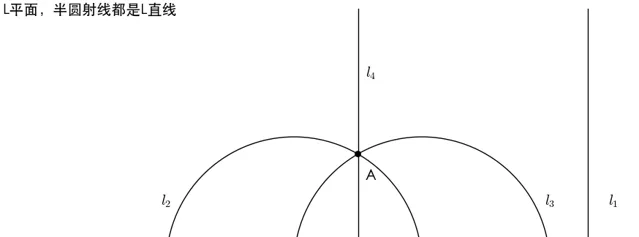
直線 l_2 、 l_3 、 l_4 都平行與 l_1
過A點可以作1條以上直線與 l_1 平行
5 平行公設不能被證明
平行公設,一個生活中似乎隨處可見的真理(三角形內角和180度等),竟然被 證明了它不能夠被證明 ,因為歐式幾何和非歐幾何都沒有邏輯矛盾。
我們來看看羅氏幾何和歐式幾何的公設的區別
歐式幾何:
公設五:同一平面內一條直線和另外兩條直線相交,若在某一側的兩個內角的和小於兩直角,則這兩直線經無限延長後在這一側相交。(等價命題:過直線外一點,有且僅有一條直線與已知直線平行。)羅氏幾何:
公設五:過直線外一點,至少可以做一條直線與已知直線平行羅氏幾何的存在就說明了平行公設不能被證明
6 並不是越簡單的命題越容易證明
並不是簡單的東西,就一定能夠被輕松的證明。甚至可以說正相反,因為條件越是簡單,可以使用的工具就越是難找,更需要證明者對數學知識有全方位的掌握。數學的三個猜想: 費馬大定理,四色定理,歌德巴哈猜想 就是很好的例子。這些有名的問題,題目看上去都很簡單,卻是世界上公認的難題。
跟著馬同學,看圖學數學,歡迎加入 馬同學圖解數學











