這篇文章想和大家分享一下Apollo 6.0中的參考線平滑演算法。參考線平滑模組在Apollo的框架中占據著非常重要的位置,我之前很長一段時間也都沒有給予其足夠的重視,在實際偵錯Apollo的這套演算法時,才發現其重要性,因此這次想深入解析下該模組。
一、參考線平滑的整體框架
在Apollo的路徑規劃中,其采用的是基於Frenet座標系下的規劃演算法,因此非常依賴於道路中心線的平滑性。而實際工程中,高精地圖給出的道路中心線的平滑性往往都不能滿足規劃模組的需求,因此規劃中是不能拿來直接用的,需要對其進行平滑操作。參考線平滑在Apollo計畫下的/apollo/modules/planning/reference_line路徑中,裏麵包含了多種參考線平滑演算法,整體框架結構如下所示。
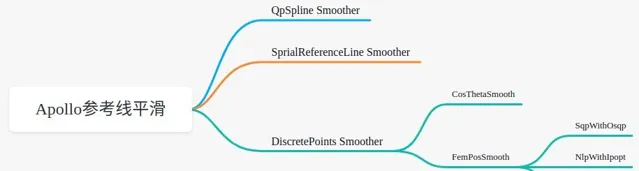
目前Apollo中共有三種參考線平滑演算法,分別為:
- QpSpline Smoother
- SpiralReferenceLine Smoother
- DiscretePoints Smoother
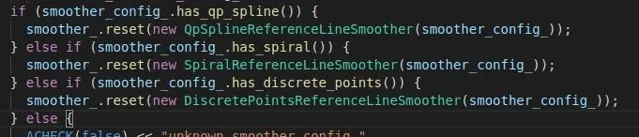
透過配置參數可以選擇需要采用的參考線平滑演算法,目前Apollo中預設配置為最後一種,基於離散點的平滑,這篇文章也就針對該演算法進行講解。
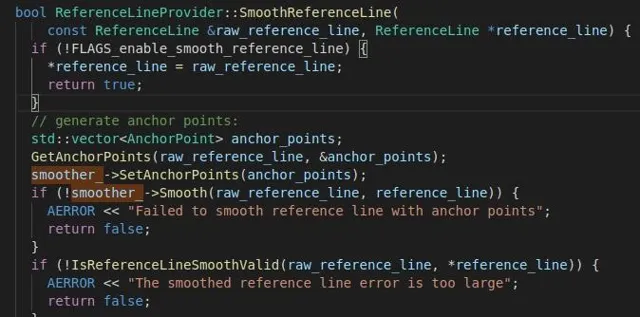
參考線的平滑函式如下圖所示,可以看出該函式的輸入為原始raw_reference_line,輸出為平滑後的smoothed_reference_line,整體的輸入輸出很簡潔。
二、設定中間點anchor points
首先第一步就是根據原始的reference_line來選取中間點,其實這一步就是根據reference_line的s值進行采樣,采樣的間隔為0.25m。采樣完畢後,就能得到一系列的ref_points,而每個anchor_point就包含了一個ref_point以及橫縱向的裕度。
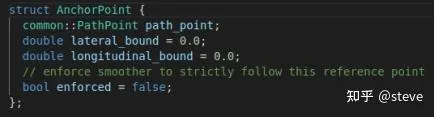
橫縱向裕度的預設參數為:
longitudinal_boundary_bound : 2.0
max_lateral_boundary_bound : 0.5
min_lateral_boundary_bound : 0.1
然後再根據自車寬度,車道邊界型別(是否為curb)等再對橫向裕度進行收縮。AnchorPoint結構中的enforced變量表示該點是否為強約束,在參考線平滑中只有首尾兩點為強約束。
計算完anchor points後,將其賦值到smoother物件中。
三、smooth函式
接下來就是參考線平滑中的主體部份,即smoother類下的smooth函式,這裏我只介紹Apollo 6.0中目前配置參數裏正在使用的discrete_points_reference_line_smoother下的smooth函式。 該方法透過對原始參考線上的離散點的有限偏移對原始參考線進行平滑。 可以看到的是,在這個類中還有兩種不同的平滑演算法,分別是:
- CosThetaSmooth
- FemPosSmooth
實際使用的演算法在配置參數裏設定,目前Apollo中用的為FemPosSmooth該演算法,後面介紹代價函式時我會展開來講下這兩種方法的區別。
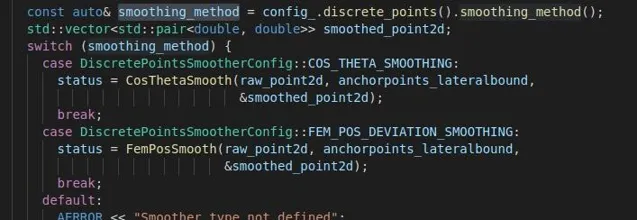
從該函式的入參可以看出,輸入為anchor_points的x,y值以及橫向裕度,輸出為平滑後的point2d。可以看出這個函式裏也沒做什麽重要的事,只是一個介面,先是將橫向的裕度進行了收縮,然後就直接呼叫了Solve函式進行問題求解。
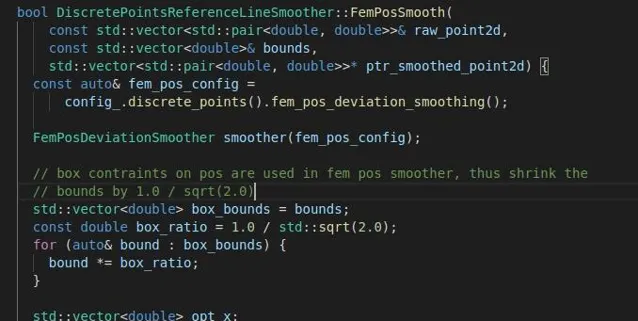
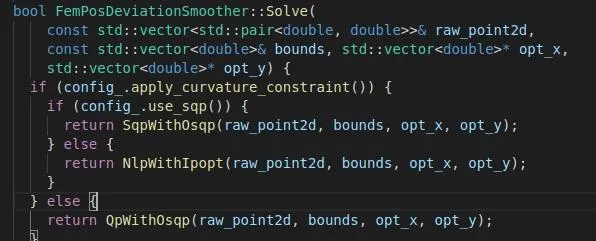
進入到Solve函式後,我們可以看到這裏又有三種求解方式(從中可以看出參考線平滑模組還是非常龐大的,也說明了其重要性),這分別是利用不同求解器實作了這個方法。如果考慮參考線的曲率約束,其最佳化問題是非線性的,可以使用ipopt非線性求解器求解(內點法),也可以將曲率約束線性化後使用osqp求解器來用SQP方法求解;如果不考慮曲率約束,則直接用osqp求解二次規劃問題。目前Apollo 6.0中預設的參數為不考慮曲率約束,這點我有點奇怪,可能是為了演算法效率方面的考慮,也可能是加入曲率約束會使得問題很難求解。後面這三種求解方式我都會介紹一下。
四、最佳化問題的構造及求解
首先講解Apollo中預設采用的平滑演算法,這裏將參考線平滑構造成了一個二次最佳化問題,並使用osqp求解器進行求解。二次最佳化問題的整體框架我想大家應該都比較熟悉了,這裏直接來看它的代價函式及約束條件。
- 最佳化變量
離散點座標(x_k, y_k)
2. 代價函式
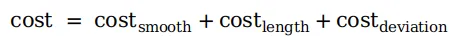
數學運算式如下所示:

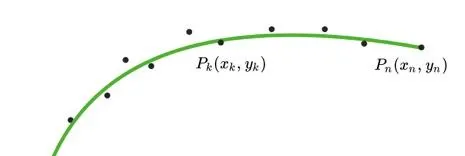
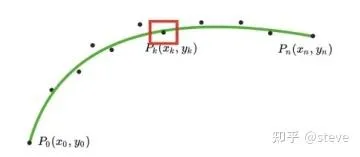
cost_smooth的物理意義可以理解為前後兩點連線向量的模平方,如下圖中的紅色向量P1P3的模平方。如果這三點在一條直線上,則這個值最小,相對應的參考線也越平滑。
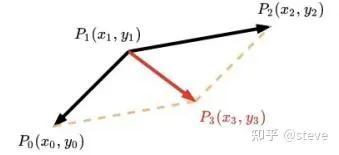
關於這項平滑度的代價,還存在其他的表示形式,例如下圖所示的相鄰向量之間的夾角theta。

假設我們擁有連續3點P0,P1,P2,其中向量P0P1和向量P1P2之間的夾角就可以表示為:
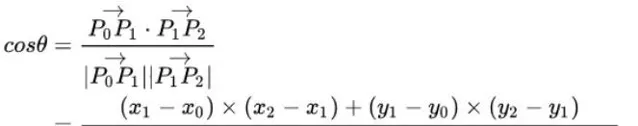
cos(theta)的值越大,theta越小,P0,P1,P2也就越接近直線,參考線也就越平滑。因此cost_smooth也可以表示為:
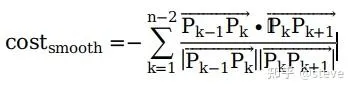
這兩種代價函式的表達形式也分別代表了上面提到的參考線平滑中的FemPosSmooth方法和CosThetaSmooth方法。可以看出後一種的cost設定為非二次型函式,因此如果采用這種方法則需要使用非線性最佳化。
cost_length 代表了離散點之間的距離平方之和
cost_deviation 代表了平滑後的離散點相對原始參考點的偏移距離平方之和
在Apollo的程式碼註釋中,用了6個點作為例子來展示P矩陣的具體形式,大家可以試著按照上面的公式來列出6點的代價函式來看看,就是其註釋中的這種形式。
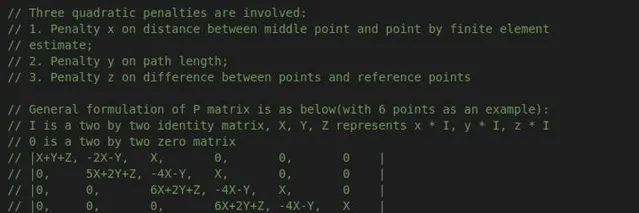
這邊還需要提到的是,如果采用的非線性最佳化來求解該問題,Apollo還增加了一個關於松弛變量的cost,松弛變量的作用在後面的曲率約束中可以看到。
3. 約束條件
第一個約束,我們希望平滑後的參考線距離原始參考線的偏移量不能太大,雖然在代價函式中,已經有了關於偏移量的懲罰項,但這只是一個軟約束,不能保證其偏離的具體數值能限制在某個範圍內。因此這裏我們添加關於偏移量的硬約束,而這裏的偏離範圍就是之前設定的橫縱向裕度構成的box內。
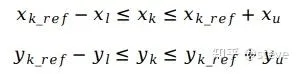
在非線性最佳化演算法中,Apollo還加入了曲率的約束。關於曲率的計算,Apollo的主要思想是三點構成一個圓來求解半徑,並且中間也設定了幾個假設:
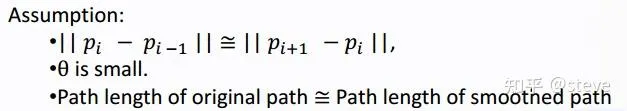
最終約束條件的構成計算為:
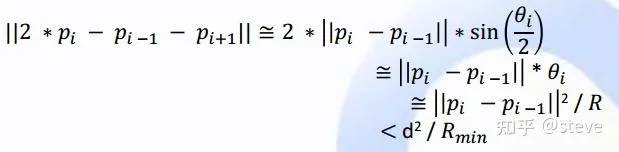
第一個近似是假設了前後兩段的長度近似相等,也就是第一個假設;
第二個近似是假設了theta值很小時,sin(theta)約等於theta;
第三個近似表示兩點間的弧長,約等於兩點間的距離,也就對應了第三個假設。
這裏的數學推導不是很復雜,大家可以畫圖出來看看就明白了。最終這個約束的上限為設定的最大曲率,即最小轉彎半徑。d表示離散點之間的平均長度,Rmin表示最大曲率約束。
為了保證有解以及求解更快的收斂,Apollo中還添加了大於0的松弛變量,因此最終的曲率約束可以表示為:
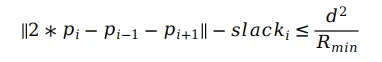
對於松弛變量,只需要保證其大於等於0即可:
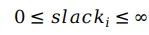
4. 曲率約束的線性化
到此最佳化問題的基本形式已經完全建立了,我們可以發現代價函式為標準的二次型,而約束條件裏唯有曲率約束是非線性的,也就意味著不能當成二次最佳化問題來求解。我們當然可以把其當做一個非線性最佳化問題來使用Ipopt進行求解,也是Apollo裏采用的一種做法。或者我們可以單獨將這項曲率約束線性化,這樣也就將這個問題轉變為了二次最佳化問題,即可使用osqp進行求解,而這在Apollo裏對應著SqpWithOsqp演算法。
曲率約束的線性化也比較簡單,直接在參考點處進行泰勒展開即可。
假設我們的約束方程式為:
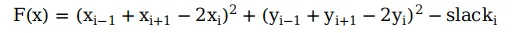
在原始參考點X_ref處對其進行泰勒展開後得:
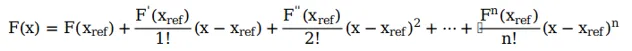
線性化只保留第一項得:
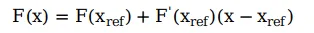
F在原始參考點X_ref處的值為:

在F(x)原始參考點x_ref的導數為:
其中:
帶入曲率約束方程式並化簡後得:
五、總結
至此,Apollo中基於離散點演算法的參考線平滑模組就全部介紹完了。整個模組涉及到的規劃演算法還是比較經典的,其主要思想都是建立在最佳化問題上,需要一定的規劃演算法和最佳化基礎來充分理解其核心。當然Apollo的演算法也不是完美的,在我們實際工程中,還需得根據實際場景來調整它的代價函式和約束條件,以達到更好的效果。歡迎各位讀者在評論區留下你們的問題及思考,大家互相交流,共同進步~ 也非常歡迎各位關註我,留言討論~
參考資料:
- 開發者說丨離散點曲線平滑原理
- steve:Apollo 6.0 規劃模組演算法解析2
- apollo 參考線平滑
- 百度Apollo程式碼閱讀:參考線平滑FemPosDeviationSmoother_荔江北的部落格-CSDN部落格_apollo 參考線平滑











