民科好多啊…… 可惜專搞 GR(廣義相對論)的幾個大牛都沒出現,只好讓我這個半民科頂上去了。
John Wheeler (費曼的老板,「黑洞」概念的提出者)有句話,請記住它:「品質告訴時空如何彎曲,時空告訴品質如何運動。」
再記住這句話:質點在彎曲時空中運動時,軌跡會受到時空彎曲的影響,就跟受到一個力一樣;人們為了方便,管這個表現叫「重力」。
夠了,剩下的就是數學了。當然,要是有人願意用民科式的腦補來填充,咱也沒轍啊。
說出「黑洞附近因為巨大的重力產生了空間扭曲」的人,放學別走。寫給外行看,也得保證措辭盡量嚴謹啊。科普也要按照基本法,識得唔識得噶?
最後,澄清兩個概念。
首先,彎曲的東西,是時空,而不僅僅是空間。在老愛之前許多年,黎曼本人就試圖用空間彎曲解釋重力:因為,自伽利略指出「重力品質 == 慣性品質」(你可以通俗地將這個等號理解為「從披薩斜塔上往下扔一大一小倆球結果這倆同時落地」,雖然伽利略其實並沒有做過這事兒)以來,人們發現,這一事實在牛頓力學的框架下實在是太不自然了(兩個不相關的物理量竟然完全相等),幾乎唯一的「看上去自然」的解釋就是「重力是幾何效應」(這使得這兩個物理量事實上成了一個東西)。可惜因為當時完全不可能對「時空」有什麽認識,黎曼沒有把時間維度放進去,所以碰了一鼻子灰(對 GR 微擾有經驗的人應該能立即想到,在弱場下,跟牛頓重力勢長得差不多的那個東西,正是出現在與時間有關的分量上)。
其次,在一般情形下,我們一般不會使用「扭曲」這個字眼。「扭曲」在 GR 裏有著特殊的內涵:不為零的撓率,也就是適應度規的聯絡張量 \Gamma^{a}_{\ b c} 的兩個下指標 b 和 c 不能交換。而通常說的「時空彎曲」,指的是時空的黎曼曲率張量不為零。有撓率的 GR 被研究得不多,部份地因為老愛在最早版本的 GR 中就假定了撓率為零而被大家因襲,也部份地因為有撓的 GR 在很多方面與觀測不符(比如,最簡單地,撓率的源是什麽?你覺得粒子自旋好使麽?)。現在有人試圖用宇宙尺度上的撓率替代暗物質,也把那張 Hubble diagram 擬合上了(當然,關於 Hubble diagram 的許多擬合都有 overfitting 之嫌,這項工作也不例外);不過,提出這個模型的人自己都說「姑妄言之姑聽之」了,大家便也沒有太認真地對待。
通俗地說,「彎曲」指的是這樣的情形:把一個向量從 Q 平移到 P,有「上路」和「下路」兩種走法(看下圖中的那個「平行四邊形」),而透過兩種走法平移過去的向量 [ 下圖中的 v_a(P) 和 \tau_a(P) ] 是不能重合的——這意味著,你好端端地試圖朝前走,時空的彎曲卻偏要來搡你一把,這「搡你一把」就是重力。

(圖片來自
http:// arxiv.org/abs/0804.3742,這是我見過的廢圖和廢話最多的物理學博士論文之一)
而若時空是「扭曲」的,則上圖中的那個「平行四邊形」根本不能存在,得缺個口兒:
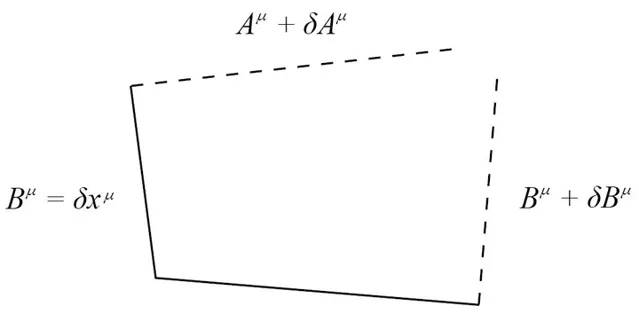
(圖片來自:
http:// arxiv.org/abs/0903.2565)











