這次談Spatical Computing(長文)
也算是【從GPU談異構(14)】吧
(♧◑ω◑)☞♡☜(◐ω◐♧) 隨性隨性
Spatial轉譯成中文,妥妥滴高大上
空間計算,當然以此對應是時間計算。
中二的你是不是立刻想打一個響指。
其實也沒錯了,你想到了他。

還有他……

沒錯,他是卷福、是福爾摩斯、是奇異博士、是圖靈
這只是他在不同時空中不同的分身
ԅ(¯ㅂ¯ԅ)ԅ(¯ㅂ¯ԅ)ԅ(¯ㅂ¯ԅ)
抖機靈結束,這是因為所有話題都脫不開下面這個起點,圖靈機和圖靈可計算。
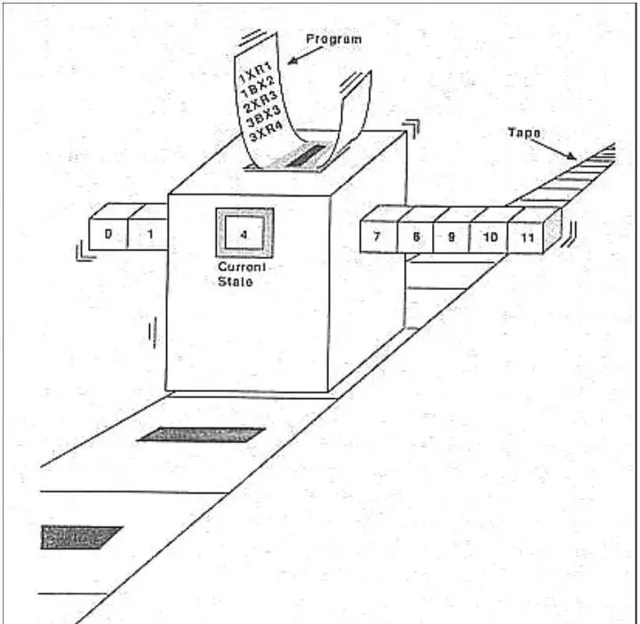
奇異博士手上的是時間寶石,能夠掌控時間。
但必須要澄清的是,在另一個電影裏,圖靈手上的其實是空間寶石。
包括很多EE甚至CS的同學都沒有明白圖靈和丘奇到底做了什麽。
他們的核心力量其實是在虛無中標定了一個空間,那是 無盡問題空間 中的 數學問題空間 中的 可判定問題空間 中的 有答案問題空間 中的 可計算空間!
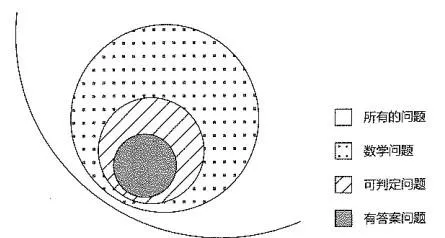
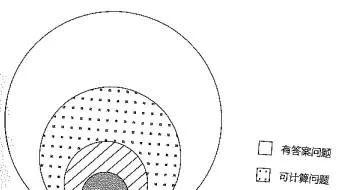
那就像是在無盡的宇宙中尋找到了地球,一個適宜CS+EE 工程師快樂成長、努力奮鬥、脫發明誌的天堂。
圖靈可計算的原理不在本文範疇,這裏想澄清的是,圖靈之後,人類有了一個判定基準,即先衡量一個問題是否屬於圖靈可計算,如果是,就可以從褲襠裏掏出圖靈機,盤它。
舉個反例,ising問題就是來自有答案空間但非圖靈可計算空間的邪惡的古爾丹。
不過,圖靈可計算只是化開了天地,肉體凡胎的程式猿又如何能上天入地呢?
這個劇本裏,真正手握時間寶石的是馮諾依曼。他長的沒我帥就不放圖了。
馮諾依曼創造了馮諾依曼架構,而在該架構執行的圖靈可計算,我們可以把它稱為temporal computing,即時間計算。
與此對應,我們通常把圖靈可計算中的非馮諾依曼架構上執行的圖靈可計算稱作spatial computing,即空間計算。
可能很多同學對這個馮和非馮的時空定義很不解,教科書不是這麽說的對吧。
我舉一個栗子方便理解,再下面就好說了。
我們可以把一個圖靈可計算問題類比為我從宇宙中心五道口出發,要到達天安門廣場看升旗的問題。
很多同學會說,咯,你開啟地圖,從這裏到這裏不就好了?
話是這麽說沒錯啦,這就是圖靈和丘奇都是數學家,而馮諾依曼是工程師的差別。你得用工程師的思維來考慮這事。
你先到哪兒? 再到哪兒? 用什麽交通工具? 要不要吃個飯? 有沒有遇到熟人? 會不會迷路?
一個真正的工程師,會考慮到所有可能的變化並給出完備的應對,最終達成mission completed。
馮諾依曼給出的答案就是折疊時間,它創立了記憶體和堆疊的概念,在發生任何事情的時候馮諾依曼架構都能夠將當前 時間狀態凍(保)結(存) ,以上面的題目為例,就像地圖折疊起來,一段一段路,都變成了獨立的行為片段(固定存檔)。
如果無事發生,那就逐段進行即可,但如果發生任何事件,都能夠時間回(讀)退讀(檔),重新出發。你可以重溫一下奇異博士的劇情,就是他打敗多瑪姆的劇情,是的,這就是馮諾依曼架構(你可以試圖把主角的面孔換成馮諾依曼)。在馮諾依曼架構下,你也可以的,甚至更進一步,來一個多執行緒的任務(多時空),你一邊在從五道口去天安門,一邊又在從陸家嘴出發去松江加班,你都可以基於時間片化身無數,單人刷完全部副本。
這就是時間計算!
這也是一個數學家和一個工程師最大的區別
數學家的直腸子想的是如何快速解決一個問題
而工程師考慮的是如何建立可以一個長期穩定的解決問題的方法,因此才誕生了馮諾依曼架構並且成為解決圖靈可計算問題最主流的硬體框架。
那麽,從工程師認可的長期穩定的解題路徑- 時間計算(馮) ,到讓工程師覺得還不那麽靠譜的 空間計算(非馮) 變得靠譜。中間需要解決什麽問題,才能獲得一個可用或者至少專用的空間計算(非馮)機器? 肯定不是簡單地把整個計算圖平鋪開啟,讓每一個人都快樂且高效地到達終點那麽簡單,要這麽簡單,馮諾依曼就是個瞎子啊。
在我的認知中,spatial computing要跨過三重大山,每重山上要過三座崖,才能算得上可用,否則永遠都只能在數學家的夢裏。
第一重山是最難的,那是:變化(divergence)spatial computing需要首先解決各種計算的變化問題。要過這重山得過三座崖,一座更比一座艱難,那分別是: 分支、遞迴、異常。
分支, 其實是最容易解決的,不就是做多選題嘛,大不了我把所有分支條件都模擬出來,也就是我把整個北京地圖全展開,你從五道口去天安門不是? 就算你去大興機場繞一圈,我也給你把計算圖布上了,而且就算你不去大興,別人總會去嘛,資源也沒白費。
註:AI的MoE就是典型的分支執行,大家訓練的時候其實就全部署上了(也有人叫他稀疏)。
遞迴, 是相對麻煩的事情,我看我家兒子就是這樣,好好走著走著,突然看到個啥,就湊過去死迴圈了……這裏的不確定性很大,沒有特別好的辦法。要解決,首先需要保持圖靈完備,這也是RISC-V在空間計算中用作PE的主要原因,其次,記憶體管理要下沈,不能在編譯器做,得到PE做,再次,祈禱唄,祈禱演算法相對沒那麽惡心,當然要真實在不行,那就偶爾來個萬爺等一孫也就忍忍算了,畢竟回憶一下,多人出遊的時候,總有一個二逼遲到不是。
註:AI的動態tensor就是典型的遞迴 但是AI的演算法都是成熟的調參俠寫的,相對沒那麽深,大多數情況都在控制範圍內。
異常 ,才是所以這個山最難跨越的關卡。難在什麽地方呢? 難在科學家不理解……
工程師和科學家經常的吵架就是:「這裏的RAS很難處理的」,「RAS對解決問題沒有收益」,「系統這麽大,出錯的機率是累進的」,「我們先解決問題,再來考慮RAS」…………
這個世界的工具,從來就沒有絕對可靠可言,都是機率,要算的。我曾經有一個貼文,有些潛在的問題,已經在逐漸變得明顯了。已經到了數學家你不能不考慮程度了。
異常是什麽呢? 還是以從五道口去天安門為例,你開車出門,想著順道去鼓樓大街看看新出的遊戲,小小分個支,沒毛病。買了新遊戲一開心你想著順便在鑼鼓巷吃點小吃,遞迴了不是,也沒多大個事。關鍵是你順手喝了兩杯酒,上車一啟動碰上查酒駕的,哦豁,異常了,進局子了。
進局子了,這事在空間計算(非馮)架構裏,沒法處理,因為整個計算狀態走到哪兒算哪兒,沒存檔,得整個重來。要僅僅是五道口到天安門還好,怕的是這其實是整個人生中的一天,那完犢子了,可能整個人生就灰暗了啊,你玩的是一命到底的地獄模式。
演算法的下一步演進,必須要逐漸考慮到對硬體的容錯性,數學家必須要能夠理解現實的殘酷,把RAS融入圖靈可計算空間的本身(縮小空間)。
註:我樂觀地期待AI的演算法能夠最快地找到這個答案,例如多路徑(MoE多專家啟用)
題外話:馮諾依曼怎麽處理前面的進局子問題呢? 存檔啊,狀態寫入記憶體唄,幹幹凈凈進局子就當在另一個世界穿越體驗一下生活唄,玩完了你讀個檔啊,狀態回到你進鑼鼓巷的時候,該吃吃該喝喝還能重新享受一下,因為你讀過書,你知道同樣的招數對聖鬥士是沒用的,你再上車,一啟動,又碰到警察! 又進局子了,原來警察也讀檔了…………終於你在局子裏進進出出幾次之後,你明白了,馮諾依曼不是聖鬥士,你得在讀檔之前搞定警察才能最終到達天安門…………
 第二重山是我跨不過的,那叫做圖編譯
第二重山是我跨不過的,那叫做圖編譯
spatial computing需要能夠對套用進行圖編譯,即編譯成圖而不是簡單的指令流。我確實沒學過編譯器,大致上只能用芯片設計的綜合工具來類比其語言轉譯和最佳化的流程
如何才能把一個圖靈可計算問題分解為計算,請教過很多人,有人跟我講很簡單,都能做,也有人說特別難,綜合各種資訊大致推理:編譯器本身學的人不多,而編譯器本身卻囊括了非常巨大的知識空間,其內部有非常多的技術分支,圖編譯及布局更屬於其中的偏門,即使菊廠號稱全中國編譯器能力第一,也並沒有囊括圖編譯及布局方面的人才。而從業界的情況來看,空間計算在美國也能有好幾家startup在做(cerebras、tenstorrent、tesla等等),但看中國大陸一家類似的startup公司都沒有,大致上,編譯器的人力配比也是如此這般吧。
這事我不是行家,也希望業界有人能指點一下。
第三重山,是互聯和通訊spatial computing相比馮機需要更加強大的片上片間的互聯通訊能力。
空間計算(非馮)和時間計算(馮)最大的不同,就在於數據流方向。
馮諾依曼架構的核心是增加了記憶體,所以資訊互動、狀態保存,都是基於記憶體為中心進行的,也就是所有的PE存取記憶體就罷了,而記憶體具有無依萊特征,也就是除非瘋狂玩鎖,PE之間的依賴關系都可以透過記憶體消除。
但非馮架構完全不一樣了,他沒有全域的shared memory,數據在PE直接傳遞,所以數據流的核心是解決PE之間的互動和依賴。嗯很多人簡單理解空間計算就是控制好PE之間互相讀寫就好,實際上,PE之間的依賴解除,防止wormhole死結才是關鍵(編譯器全預分配記憶體也能解死結,但我覺得那樣編譯器負擔和約束太大)。
我還沒有完整地跑過一顆大號的空間計算芯片,所以這重山我並不能說邁過了。但我是做互聯技術出身的,在業界玩互聯怎麽說也算是第一陣營,這山再高,熱熱身向上沖就是了。
我們也可以看看業界怎麽解決這個問題的
(๑> <๑)
graphcore是個很有趣的例子,它使用了BSP編程模型,這裏不深度解釋BSP的原理,簡單來講就是它把計算和通訊分割成獨立phase,這樣依賴關系就被完全打破了,寫演算法也變得簡單,順著節拍,來,藥藥藥,切克鬧……
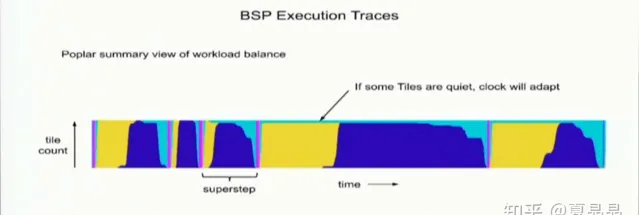
BSP計算模型的創始人Bill McColl也就在菊花廠任職,聊過,數學家,對這個演算法很自豪。但是作為一個工程師,我對他是無語凝噎。
這種計算模式,數學家是舒服了,工程師都在吐血。
這種全域同步啟動和停止的方式,這負載變化引發的巨大的電流變化最終一定會觸發電壓無法穩定,這對系統的電源完整性是極大的挑戰! 大家都知道關燈一小時活動吧? 極其反智,幸好跟著玩的人還不多,等什麽時候歐洲的白左們都信了,把工業電也跟著一起玩,我就坐看歐洲發電、變電站放煙花了。
graphcore也是如此,這顆芯片我估計其啟停之間的高頻電源雜訊得有100mV,除非客製電源模組(響應時間小於5us?),並且編譯器控制好啟停的mininal period,並且在exchange phase有意拉高Vdd以備PE啟動的IR drop,否則根本玩不轉,而即使玩轉了,能耗表現也是有破綻的。
相反tenstorrent則采用了另一個劍走偏鋒的技術路徑。我曾經形容,groq的芯片是把整SOC大芯片做成了一個單核CPU,而tenstorrent則是把他的SOC大芯片做成了內含120個小SOC的松散聯盟(wormhole為例),它的每個核,其實都是cpu+mem+NIC的完整體,編程上,采用了actor模型,我覺得這是一條正確的道路。按照自媒體的風格,喊出:jim keller一級棒,就好了。

要做一個可用的spatial computing,我講了有這麽多困難,這麽多重山要跨越,那麽問題來了。
為什麽我們要做spatial computing呢?
價值是什麽? 繼續用馮諾依曼架構它不香嗎?
OK,讓我們還是回到patterson教授講述DSA時候的底片,想一想他神秘的微笑。
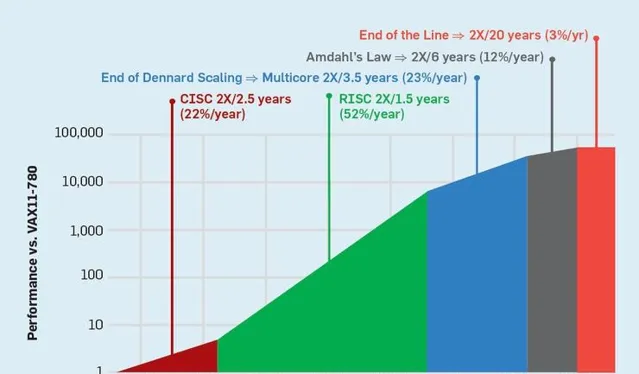

一、spatial computing是一種DSA,因為它沒法像馮諾依曼架構那樣的普適性,它大機率也只能解決一部份的問題,但效率會更高。
二、AI即神經網路的形態,更接近於計算圖的形態,只要數學家們真正認識到硬體容錯性的重要性,在演算法中支持了容錯,MoE、動態shape反而都是能夠客服的問題。
三、也是最重要的一點,馮諾依曼架構效能提升的黑色地帶Amdal's Law還有肉眼可見將來的memory wall。spatial computing是可見的能夠突破Amdal's Law和memory wall,持續擴充套件算力的唯一路徑。在空間計算的範疇下,問題的復雜度也不再依賴於莫耳定律,僅僅依賴於系統規模是否與問題規模匹配,也就是這只是一個充錢的問題

極端腦洞下,你甚至可以制造一個spatial computing的戴森球電腦。
有同學對我的觀點有些誤解,總結一下。
我是支持並希望去挑戰spatial computing的,雖然我前面講了那麽多困難,異常、圖編譯器,都是電腦體系結構中世界級的難題。但不能因為他們難就退縮啊,因為這些題目難,還沒有難到無解,而amdal law和memory wall那是讓人絕望的困難。
只要你跨越前面提到的這重重山,你所能得到的,那是無盡的寶藏。











