@看風景的蝸牛君 的回答從幾何方面來論證了不太可能看到昨天的影像。我下面就從能量的角度來進行論證,說明從能量的角度來看也是不太可能的。
當光垂直照射到物質上時,幾乎不可能是百分百反射的。因為光會不可避免地與物質發生交互作用。比如物質中的電子會被光激發到較高的能階,隨後可能以熱放射線的形式回到基態,從而導致損失等等。
金屬鏡子的反射率可以用 Hagen–Rubens 關系來大致描述 [1] :(沒有本征吸收的情況下)
R\approx1-2\sqrt{\frac{2\epsilon_0\omega}{\sigma}}=1-4\sqrt{\frac{\pi\epsilon_0\nu}{\sigma}}
其中 R 是反射率, \omega 是入射光圓頻率, \nu 是入射光頻率, \epsilon_0 是真空電容率為 8.85\times10^{-12}\ \rm F⋅m^{-1} , \sigma 是金屬的電導率
已知導電率最好的金屬是銀 [2]
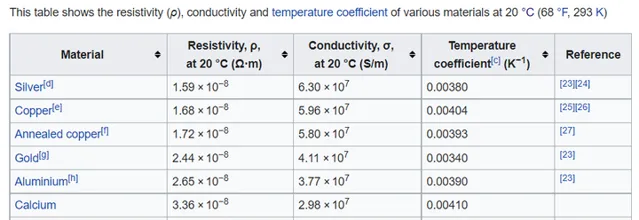
那麽我們可以計算出780 nm時(可見光範圍內頻率最小,為 3.85\times10^{14}\ \rm Hz )銀的理想反射率大約為 95%
實際的銀鏡反射率比計算值略好,可以達到99%。比如下圖是來自於Thorlabs的數據。
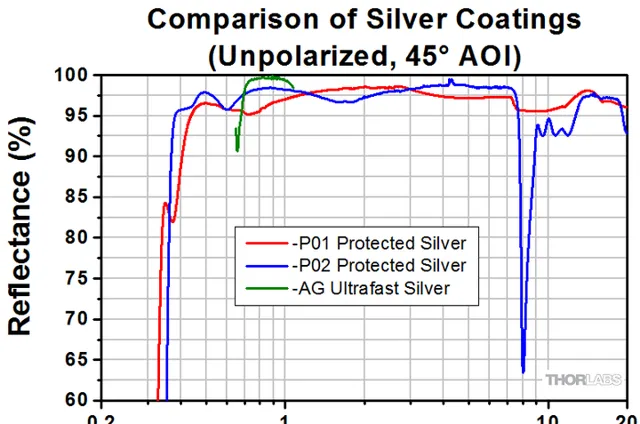
而一些特殊的dielectric mirror,其反射率甚至最高可以達到99.999%! [3] 下面我將會論述,哪怕反射率突破目前的極限達到了6個9,也會因為能量損失而無法提供能看到昨天的能量的。
假如兩個鏡子之間的距離是10公尺(距離增加將會不利於幾何關系,距離減小將會不利於能量關系,在此取10公尺)
那麽24小時前的光已經反射了 \frac{c*t}{d}=\frac{3\times10^8\times3600\times24}{10}=2.6\times10^{12} 次
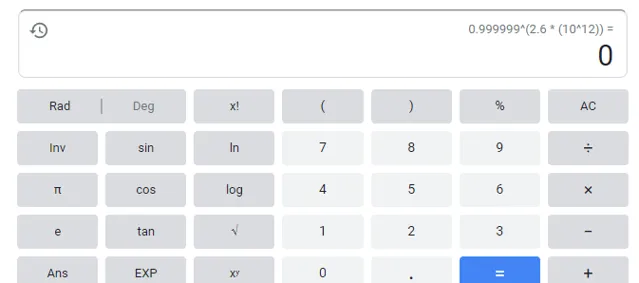
假設反射率高達99.9999%,那麽經過 2.6\times10^{12} 次反射後,剩下的能量為…… 額,谷歌小算盤精度不夠算不出來。。。(可以有人教我這裏如何估算麽?我只知道因此次數過高,沒法簡單用泰勒展開計算。)
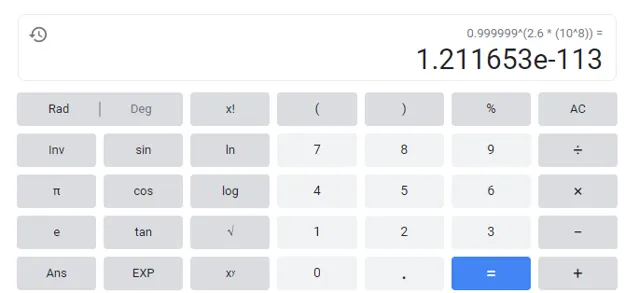
實際上,當僅經過了 2.6\times10^{8} 次反射後,也就是8.6秒後,能量就降低到只有最初的 10^{-113} 了。這是什麽概念呢?全宇宙的總能量約為 4\times10^{70}\ \rm J [4] ,全轉化為780 nm的光子( 2.55\times10^{-19} \ \rm J ),就是 1.57\times10^{89} 個光子。哪怕全宇宙的能量都照射過去,哪怕反射率已經達到了驚人的6個9,經過不到8秒後就甚至連一個光子都不剩了,更別提昨日重現了。
那麽假設對於一般的99%的銀鏡,經過100次反射( 3\ \rm \mu s )後,能量就衰減至只有37%了;經過 30\ \rm \mu s 後就只剩下0.004%了。由此可見,企圖使用鏡子實作昨日重現,從能量的角度看,是完全不現實的了。這也是為何無法使用兩個平行的鏡子來儲存光。
參考
- ^https://en.wikipedia.org/wiki/Hagen–Rubens_relation
- ^https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity
- ^https://en.wikipedia.org/wiki/Perfect_mirror
- ^https://zh.wikipedia.org/wiki/数量级_(能量)#大于1027











