惡老師秘制數學小漢堡,富含維生素abcdefg,大體難度不超過★★★☆☆,非常適合智力中等及以上人類食用。

強行摻入微量 初等數論 ,用以提鮮,劑量極小絕不致死……


儀式完畢,正文馬上開始!^_^
弱弱鬥膽說一句:本答案應該是目前所有回答裏最全最細致最明白的,寫作中途我也遇到了困難整整想了3天才解決。
說實話這個問題看似極其簡單,深挖起來簡直深不見底。
本文從計算1/49迴圈節這樣小學生都會的難度,一直層層遞進,帶你穿過歐拉定理,直至觸碰到世界未解數論難題,這其中的冒險實在是非常刺激,一路上我已經為大家披荊斬棘,難度壓到最低,歡迎來我的數學胎教樂園玩耍!^_^(強行誘捕上車)
全文手碼為愛發電!!望點贊!!有任何bug歡迎指出,因為我寫字真的特別粗心,復制黏貼都會弄錯的那種,感謝!!!
(文末有彩蛋福利,請大家堅持看完!)
!!重要更新!!
關於正整數倒數迴圈節長度問題,我已經有了更為一般性的解答!!歡迎取閱!!
趣味詳解版:
無情精簡版:
如果你的數學基礎比較差,建議先閱讀本文哦~~~
〇、你的小算盤不對勁,你更不對勁(難度:★☆☆☆☆)
首先我真的要吐槽題主,你那個小算盤螢幕太小了,連1/49的迴圈節都顯示不完整,你看看我的大屏小算盤效果多好:
而且題主的描述也很不對勁:

所以你以為回答就到這裏結束了嗎?
天真!!!
惡老師的數學胎教~才剛剛開始!!!寶貝們快快上車!
一、1/49,沒在怕的!(難度:☆☆☆☆☆)
有一件事情是肯定的:能寫成分數的必是迴圈小數(不迴圈小數可以看作迴圈節為0),並且迴圈節出現是因為余數有限(余數的數量必然小於除數)。
所以看到1/49,真沒在怕的,它余數的數量不可能超過49,迴圈節位數也不可能超過49。
盡管你的小算盤不行,但是你的手行啊!
筆算一下1/49的小數部份,很容……很難嗎?!
二、嘻嘻,1/49其實是一個2位有限小數(難度:★☆☆☆☆)
這個很有意思,並且我看了下,好幾個回答已經提到了,但奇怪的是,點贊不多,估計是很多人腦子沒轉過來。
所以我再講解下,在7進制的胎位下,你懷的崽子只有7根手指,他的世界裏就是逢七進一,十進制的6還是6,十進制的7卻成了10,49正好是7的平方,所以十進制的49就是七進制的100,化成分數1/100=0.01。
明白了吧?
不過正經人誰用7進制啊,你考試敢用7進制答題嗎?
不敢吧!
所以我們還是得老老實實地回答這個問題:
為什麽在10進制下,1/49寫成小數,迴圈節那麽長呢?有什麽辦法能夠分分鐘算出迴圈節長度嗎?
這,才是一個好問題。
三、配一把萬能鑰匙(難度:★☆☆☆☆)
對我來說,如果要確定迴圈節的長度,就必須先搞明白,任何一個迴圈小數寫成分數應該是什麽樣子——這就是我要配的鑰匙了。
為了方便,這邊只考慮 純迴圈小數 ,就是從小數點後第一位就開始迴圈。
顯然,在10進制下,純迴圈小數分母的因數不能包含2或5,舉幾個例子:
1/7的分母既不包含2也不包含5,所以它是純迴圈小數0.142857 142857 142857...;
1/27的分母也是既不包含2也不包含5,所以它也是純迴圈小數0.0370 0370 0370...;
1/15的分母包含5,所以它是混迴圈小數0.066666...,它可以看作純迴圈小數2/3=0.666666...的十分之一;
1/6的分母包含2,所以它也是混迴圈小數0.166666...,它可以看作是上面的1/15再加上0.1。
因為在本問題中,主要目標是確定迴圈節位數,所以就把混迴圈小數踢到一邊,只需管好純迴圈小數就夠了。
現在,我們設這個純迴圈小數的 迴圈部份 為 k_{1}k_{2}k_{3}...k_{m} 。
迴圈小數,感覺沒完沒了,怎麽樣和幹凈利索的分數產生關系呢?
當然是得想辦法 消掉迴圈小數的迴圈部份 呀!
這個辦法就是錯位相減法。
比如5/11的迴圈部份是45,就給5/11乘上100讓它小數點移2位,然後和5/11相減,迴圈部份就沒啦!效果立竿見影:
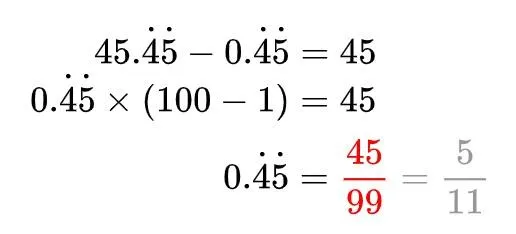
觀察一下上式規律,我們就可以打造出「純迴圈小數化分數」的萬能鑰匙了:
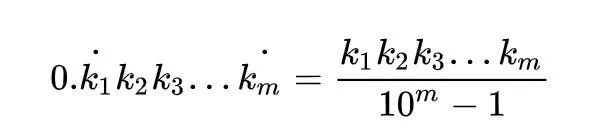
好了,現在就用這把鑰匙,把1/49變成迴圈小數的形式:
1/49的分母49的因數,既沒有2,也沒有5,判斷1/49一定是純迴圈小數,所以可以套用這把萬能鑰匙,把1/49寫成這樣的分數形式:\frac{1}{49}=\frac{k_{1}k_{2}k_{3}...k_{m}}{10^{m}-1}
四、歐拉~o了?!(難度:★★☆☆☆)
剛剛我們已經得到了: \frac{1}{49}=\frac{k_{1}k_{2}k_{3}...k_{m}}{10^{m}-1} 。
為了讓式子更簡潔,我們來把這個式子變個樣:
10^{m}=49\times{k_{1}k_{2}k_{3}...k_{m}}+1
這時候,就可以發現,這個式子是在說: 10^m除以49余數為1 ,即: 10^{m} mod49=1
我當時就胎動了一下,感受到了歐拉定理的召喚,趕緊把式子寫成:
10^{m}\equiv1(mod 49) ,即10^m與1對模49同余
很快啊!我趕緊和歐拉定理對接,歐拉定理長這樣:
a^{\varphi(n)}\equiv1(modn) ,即 a^{\varphi(n)}\ 與1對模n同余
你看看!前面那式子是不是和歐拉定理親生的一樣!
眼看就順產成功了,還楞著幹啥呀,趕緊把n=49代到歐拉函式\varphi(n)=n(1-\frac{1}{p_{1}})(1-\frac{1}{p_{2}})(1-\frac{1}{p_{3}})...(1-\frac{1}{p_{k}}) 裏!
\varphi(49)=49(1-\frac{1}{7})=42
我當時一看到42就以為哦了完事了,畢竟前面我的大屏小算盤算出了m也的確是42沒錯。
然後我想當然地以為m= \varphi(n) ,準備文章收尾的時候,突然感到不對勁:
如果迴圈節長度 m=\varphi(n) ,根據歐拉函式特性當n為質數時 \varphi(n)=n-1 ,但尼瑪1/3的迴圈小數位顯然是1不是2啊!!!!!
我這時候慌了,趕緊翻了下這個問題下的其它回答,看到有幾個提到結論是m是 \varphi(n) 的因數,再一算,n為質數43的時候, \varphi(n)=43-1=42=\varphi(49) ,也就是說1/49和1/43的歐拉函式都是42,但1/43的迴圈節長度不是42,而是21!我當時就楞了,哪裏錯了?
嗯……我老實交代,上面那個問題居然讓我想了2天,因為我誤以為是前面萬能鑰匙那一步m設得有問題,驗算了n遍,我以為我是傻,後來我才突然發現,我是瞎……
我竟然看著 10^{m}\equiv1(mod 49) 和 a^{\varphi(n)}\equiv1(modn) 想當然地以為 a^{42}=10^{m} ,但事實是 a^{42}\equiv10^{m}\equiv1 (mod49)
這兩個式子意思天差地別!前者 a^{42}=10^{m} 意味著m只有唯一解42,後者 a^{42}\equiv10^{m}\equiv1 (mod49) 意味著m的解不止一個,即m可能為42因數中的任何一個,m為1、2、3、6、7、14、21、42的其中一個!
所以光用歐拉定理還是不能完全確定m的值啊!!
偏偏這個42的因數還特別多,煩死了!!!(TAT),怎麽辦啊!!!列舉法我是拒絕的!!!更可惡的是這個問題看起來貌似極其簡單……
五、冒險越來越深入了……(難度:★★★☆☆)
高能預警:這段的難度主要在於術語理解,邏輯是很簡單,難度相當於中國人看美國八卦報紙,你英語好看起來很容易,都是家長裏短的破事,你英語菜看起來不知所雲以為是什麽高大上的東西。
溫馨提示:這段對沒有數學基礎會有難度,可以直接跳到六,六是真刺激。
最終我又花了1天時間現啃了一堆資料,就硬啃,最終終於明白事情如此簡單:
我要求的m,被稱為「10模49的階」。
抽象吧?不準下車,車門已經焊死了,你就陪陪我走到底吧!我這3天簡直就像在黑暗裏獨自前行,永遠不知道下一個坑在哪裏!
嗯,回到剛剛那句話,「10模49的階」,你就當閱讀理解做,這其實不是一個數學題,而是一個語意瘋狂套娃的腦筋急轉彎!
「模「沒什麽好說的,就是取余數,至於這個」階「是什麽,真得好好解釋下:
對於歐拉定理 a^{\varphi(n)}\equiv1(modn) ,當a和n互質(這句條件等價於1/n為純迴圈小數),此時滿足 a^{x}\equiv1(modn) 的x存在最小正整數解,這個x稱作a模n的階,並且這個階要麽等於 \varphi(n) ,要麽是 \varphi(n) 的因數。
別慌,這句話的關鍵詞就兩個字「因數」。這足以一半解答了我們的疑惑。前面我們發現,1/49和1/43的歐拉函式同為42,但1/43的迴圈節長度為21,本質是因為迴圈節長度並不等於歐拉函式的值,而是這個值的因數,也就是說,目前的全部推理,只能確定它倆的迴圈節長度為1、2、3、6、7、14、21、42的其中一個,只不過1/49的迴圈節長度正好落在了最大值。
那麽問題來了,這「階」怎麽求呢?哎,這時候又必須要談「原根」:
若a模m的階等於φ(m),則稱a為模m的一個原根。
這句話對於大多數人來說應該還是天書,但其實數學證明很多時候就是顛來倒去說同一件事。
可以肯定的是,10是模49的一個原根,且它的階正好就是 \varphi(49)=42 ,所以1/49的迴圈節長度是42。
那麽問題來了,有什麽 \varphi(n)=42 ,階卻不是42的n呢?
因為 10 不是 43 的原根,所以 10模43的階不是42,是21。
至於原因,我已經在開頭給出的連結中非常詳細解答了,歡迎大家閱讀!!
六、後記
因為我是業余學習的數學,數論也是因為覺得這個 1/49 的問題有趣,臨時學的
所以一開始我幾乎沒有任何知識儲備,甚至天真地以為對於任意正整數 x ,人類應該已經有一個確定的什麽函式 f(x) 可以無需列舉就能得出 1/x 的迴圈節長度,但到處都搜不到答案,
於是我就開始「閉門造車」,研究了很久,一直發現沒有結果,這個過程非常煎熬
最終透過自己持續不斷的思考,終於發現這個問題最終指向了一個終極難題:大數分解,本質上觸及了黎曼猜想(關於這一點,我在開頭給出的連結也詳細解答了)
——嘻嘻,那我解不出也是理所應當的嘛!
這樣的經歷給我帶來非常神奇的體驗,以下是當時的心情記錄:
……我就想辦法自己找這個函式,因為我感覺這個問題看起來極其簡單,詭異的是我研究了一整天都沒找到辦法……我仔細翻看了這個問題下的所有答案,竟然沒有人能解答我的問題。
難道……是我的問題太簡單了嗎?
我呆呆地寫了十頁紙,反反復復驗算,希望不斷被點亮、熄滅、點亮、熄滅,我逐漸感嘆自己是不是智商不配碰數學,這麽簡單的問題,算不出來一定是因為我太笨了……
我很明顯感覺到自己在一個怪圈裏打轉死都出不去。這種感覺非常恐怖,就好像在一片漆黑的森林裏尋找回家的路,走了很久發現自己還在原地,感覺永遠沒有出頭之日,然而心底卻又有一個聲音不停和我說,你再撐一下就到家了!
最終,我還是放棄了,我承認自己不行,於是拿手機刷了很久亂七八糟的東西放松,然而我滿腦子都是那個問題,根本揮之不去,於是我開啟電腦不停換關鍵詞搜,我先是在一篇小論文看到了一個叫做Artin猜想的東西,我突然意識到了什麽,讓我喜出望外,但那也不是我要的的東西,我繼續不停檢索,終於突然搜到了「最小正原根上界問題」,我感覺希望之光又被點燃,趕緊看下去:
華羅庚於1942年套用狄利克雷特征函式的概念及三角和的估值方法,在估計最小正原根的上界方面,得到了很好的結果,他證明了:g(p)<2^r*p^(1/2),其中r是φ(p)=p-1的不同質因數的個數。
1959年,王元證明了g(p)=O(p^(1/4+ε))。
(可能我沒有找到最前沿的資料,但這個問題似乎真沒有完美解決,求大佬給我一個痛快)
我瞬間站了起來,我和我老婆說我竟然自己發現了世界級的數論難題!
我老婆正在忙她的畫,似乎一下子沒明白我在說什麽。
我就和她說:「可能你不知道我在說什麽,但我依舊想和你傳達我的喜悅。」
我老婆就像往常一樣誇我:「老婆太強了!」
盡管我此時可以為我的小聰明歡呼,但事情卻細思恐極……
我,追隨著一只1/49的美麗蝴蝶,等我撲到它,又出現一只蝴蝶1/43,這時我發現剛剛抓到的1/49蝴蝶又逃跑了,我就一路追過去,越來越累,卻還是不停跑,等我反應過來才發現,四周早已漆黑一片,我努力尋找人的蹤跡,找了好久好久,才看到有人立了一塊牌子:「恭喜你到達邊界,我們都沒有走出去,你想再挑戰一次嗎?」
我的直覺告訴我趕快跑,不要在這個地獄一樣的邊界逗留!我一邊跑,周圍的風景一邊回溯,一群質數的蝴蝶開始飛舞,一會兒組成最小原根上界猜想,一會兒組成Artin猜想……一會兒又是大數分解難題,一會兒又是黎曼猜想……
這玩意不是胎教,這玩意有毒啊啊啊!!!!
小惡、收刀入鞘、全身而退吧!!
突然間,我放下執著,一切都恢復了往日的平靜。最近缺乏睡眠的我,只感覺渾渾噩噩,一想起這三天的經歷,宛如做了一個荒唐的夢。
……恐怖如斯,不可名狀!起點如此簡單,只不過是自然數而已,並且我的每一跨步都不大,卻只消五步就踏到了學術的邊界……這種空間的失控感,簡直詭異至極!
ho!原來數論就是數學的五步蛇!!!23333
~~ ★壓壓驚:傳統美德之 文末福利 ★ ~~
以下是我寫這篇文章的內心戲:



總之,這次神奇的經歷,讓我與數學結下不解之緣
我決定投入更多的時間學習數學
目前在蝸牛般自學數學分析和抽象代數,我對這兩個分支非常感興趣
在學習過程中的任何見解,我都會無條件地分享給大家,共同進步~~










