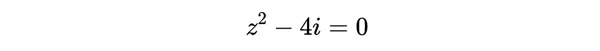天才高斯——19世紀最偉大的數學家,近代數學的奠基者
2022-01-04知識

卡爾·佛烈德利赫·高斯(1777~1855)是一個神童。19歲差一個月的他作出了一項非凡的發現。2000多年以來,人們知道如何用直尺和康伯斯作等邊三角形和正五邊形(還有其他的正多邊形,其邊數是2、3、5的倍數),但不知道如何作出邊數為質數的正多邊形。高斯證明,正七邊形也能用直尺和康伯斯作出。
高斯透過寫日記來紀念他的發現,在接下來的18年裏,他在這本日記中記下了他的很多發現。他還是一個學生的時候就獲得了很多成功。其中有一些是對歐拉、拉格朗日及其他18世紀數學家們已經證明的定理的重新發現;有很多是新發現。在他學生時代的更重要的發現中,我們可以挑出
最小平方法
、
數論中二次互反律的證明
,以及他對
代數基本定理
的研究。他獲得了博士學位,學位論文的標題是【關於所有含一個變量的有理代數整函式都能分解為一次或二次實因子的定理的新證明】。這是他一生中所發表的代數基本定理的4個證明當中的第一個,在這篇論文中,高斯強調了在證明這個定理的過程中證實至少有一個根的重要性。下面的說明可以顯示他的思路。
我們可用圖示的方法解方程式
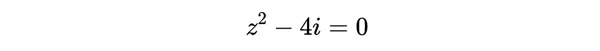
證明存在一個復數值z=a+bi滿足這個方程式。用a+bi取代z,並分開方程式中的實數部份和虛數部份,我們就得到a^2-b^2=0和ab-2=0。把a和b解釋為變量,並在同一座標系中畫出這些函式,一個座標軸代表實數部份a,另一個座標軸代表虛數部份b,我們就有了兩條曲線;一條由直線a+b=0和a-b=0構成,另一條由等軸雙曲線ab=+2構成。
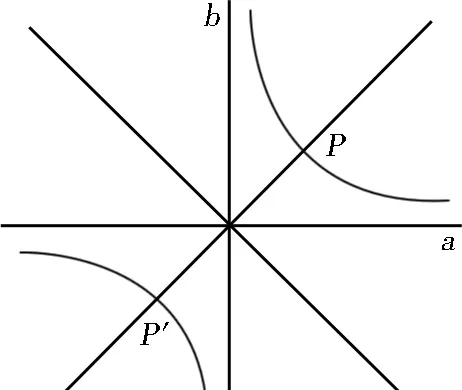
很顯然,這兩條曲線有一個交點P在第一象限。我們應該特別註意,第一條曲線的一條分支沿著θ=1π/4和θ=3π/4的方向離開原點;第二條曲線的一條分支漸近地向著θ=0π/4和θ=2π/4的方向移動;交點在最後兩個方向θ=0和θ=π/2之間。這個交點的a和b的座標是方程式z^2-4i=0的一個解的實數部份和虛數部份。假如我們最初的多項式方程式是三次而不
< style data-emotion-css="1cspyqe">
.css-1cspyqe{position:absolute;width:100%;bottom:0;background-image:linear-gradient(to bottom,transparent,#ffffff 48px);}
< style data-emotion-css="fxar0w">
.css-fxar0w{box-sizing:border-box;margin:0;min-width:0;height:110px;-webkit-box-pack:center;-webkit-justify-content:center;-ms-flex-pack:center;justify-content:center;-webkit-align-items:flex-end;-webkit-box-align:flex-end;-ms-flex-align:flex-end;align-items:flex-end;display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;position:absolute;width:100%;bottom:0;background-image:linear-gradient(to bottom,transparent,#ffffff 48px);}
< style data-emotion-css="1blqfh0">
.css-1blqfh0{font-size:16px;color:#09408e;margin-bottom:26px;-webkit-letter-spacing:0.4px;-moz-letter-spacing:0.4px;-ms-letter-spacing:0.4px;letter-spacing:0.4px;}
< style data-emotion-css="8kn4zf">
.css-8kn4zf{margin-top:0;}
釋出於 2022-01-04 05:48
< style data-emotion-css="ch8ocw">
.css-ch8ocw{position:relative;display:inline-block;height:30px;padding:0 12px;font-size:14px;line-height:30px;color:#1772F6;vertical-align:top;border-radius:100px;background:rgba(23,114,246,0.1);}.css-ch8ocw:hover{background-color:rgba(23,114,246,0.15);}
< style data-emotion-css="1xlfegr">
.css-1xlfegr{background:transparent;box-shadow:none;}
< style data-emotion-css="1gomreu">
.css-1gomreu{position:relative;display:inline-block;}
數學