不要總是糾結於小數的無限迴圈還是不迴圈。
小數只是數的一種表現形式而已,並不是數的本質。比如你題目中用來舉例的1/17。你別看它寫成小數是亂七八糟一大堆,那不過因為我們所用的小數是十進制數的緣故。如果換成是17進制的小數,不就寫成0.1了嘛!同理,65/17也就寫成了 3.E(用A-G表示10-16)!是不是一點都不亂?你想想,歸根結底是由於人類碰巧長了10跟手指頭,所以我們才用了10進制。若換成是另外一個星球上的智慧生命,長了三只手、21根手指的,人家可能就用21進制數呢。Get it?
所謂有理數,就是能寫成 \frac{m}{n}(m\in Z, n \in Z, n\neq 0) 的數。我們遇到一個數,不能這麽表示的,那它就不是有理數。
好比我們可以證明 \sqrt{2} 不是有理數。
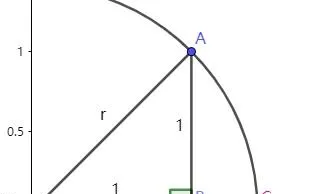
如上圖,根據畢達哥拉斯定理,
\begin{align} r^2 =& 1^2 + 1^2 \\ r =& \sqrt{1+1} = \sqrt{2} \end{align}
我們假定r是有理數,那麽它就應該可以寫成整數比上非零整數的形式。又因為所有的分數都可以化簡為互質數的比。我們就可以把 r 寫成分子分母互質的最簡分數 m/n。
\begin{align} & r = \frac{m}{n} \\ & r^2 = \frac{m^2}{n^2} = 2\\ & m^2 = 2n^2 \\ & \because 2n^2 為某整數的二倍,因而必為偶數\\ & \because 奇數的平方為奇數,偶數的平方為偶數\\ & \therefore m 為偶數\\ & 令 m = 2k , 則 k 必為整數\\ & 2n^2 = (2k)^2 = 2^2k^2 = 2\cdot 2k^2\\ & n^2 = 2k^2\\ & \therefore n 也是偶數\\ &\therefore m 與 n 不是互質關系\\ & \therefore r 不是有理數 \end{align}
\sqrt{2} 不是有理數,然而如上圖所示,它又能透過尺規作圖法被畫在數軸上(C點)。也就是說,他在數軸上的位置是 明確 的。
你之所以糾結於沒完沒了的小數點後的數位,是因為沒有認識清楚,小數本質上是就是一種變了形的分數。
a.bcdef... = a + \frac{b}{10}+ \frac{c}{100}+ \frac{d}{1,000}+ \frac{e}{10,000}+ \frac{f}{100,000}...
有理數的和還是有理數。
所以根本上,小數就不能(或者不能確切地)表示無理數。我們硬要把無理數,比如\sqrt{2} ,寫成小數的形式,寫出來的就只能是近似值。
既然一個無理數在數軸上的位置是明確的,我們就能找到略大或略小於它的有理數。有理數是可以寫成小數的,借助逼近它的小數,我們就能夠直觀地感知到它的值大約是多大。
你看,分數31/71 和 137/311 究竟誰大於誰, \sqrt{731} 和27又是誰大誰小,是不是很難判斷?換成小數,\frac{31}{71}\approx0.437,\frac{137}{311}\approx0.440,\sqrt{731}\approx27.037 , 是不是就一目了然了!
我們社會的各個領域中都普遍使用小數,就是因為它直觀。但是,正如我一開始所說的那樣,不要把形式跟本質搞顛倒了。31/71 只是約等於 0.437,它的本質是71份裏取31份; \sqrt{2} 只是約等於1.414,它的本質是面積為2的正方形的邊長。











