相對論數學原理（一），為什麽首先要解決數學問題

這個世界最不可理解的事情是，它竟然是可以理解的。

在二十世紀的頭幾年裏，艾伯特·愛因史坦 徹底改變了我們對物理世界的理解。1905年，他提出了狹義相對論，這一理論徹底地破壞了長期存在的關於空間和時間本質的科學和常識假設。例如， 同時性 ： 新理論意味著對一個觀察者來說發生在同一時間的兩件事很可能會在另一個觀察者的不同時間發生。從此以後，空間和時間不能再被看作是獨立的絕對的量。相反，它們合並了成為一個新的單一實體，稱為 時空 。此外，物質和能量也被結合在一起，形成了物理學中最著名的方程式之一：

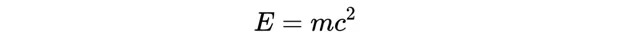
這是激進的理論，但更多的東西還在後面。狹義相對論研究的是在沒有重力的情況下物體和光的運動。兩百多年來，牛頓的萬有重力理論已被證明具有驚人的準確性。它可以精確計算下落的杯子或繞軌域執行的行星的運動。但是，盡管有巨大的實際套用，牛頓的理論與狹義相對論並不相容（牛頓的重力是瞬時的，而狹義相對論強加了一個自然的速度極限 ——光速）。

愛因史坦又花了十年時間來調和重力和狹義相對論，得出了他的廣義相對論（於1916年發表）。廣義相對論將重力解釋為大品質物體附近時空彎曲的效應。它精確地描述了很多現象，如行星軌域的非牛頓偏差、重力時間膨脹、光的重力彎曲和紅移 。它還被用來預測黑洞的存在和性質，是現代宇宙學的核心——研究宇宙的歷史和結構。在適當的條件下，廣義相對論可以簡化為狹義相對論和牛頓理論。

狹義相對論和廣義相對論可以概括如下：

或者，更簡潔地說，物理學家約翰·阿奇博德·惠勒 的名言是：

物質告訴空間如何彎曲，空間告訴物質如何運動。

天體物理學家金·格裏斯特說：

大多數物理學家都不研究廣義相對論，因為它只與牛頓的重力理論不同，與狹義相對論 也只是在少數情況下有所不同。但GR（廣義相對論）是自然的選擇——每當GR不同於牛頓時，GR就被證明是正確的。這就是大自然的運作方式，需要對物理現實進行徹底的反思。

簡而言之，相對論是人類理性的勝利，因此值得去了解和掌握。然而，要真正理解這個理論的基礎，我們必須解決一些相當有挑戰性的數學問題，這就是這個系列將要嘗試做的。下面是這個系列將要討論的關於相對論的數學原理 ：

1. 介紹必要的基礎數學，從基礎開始函式的定義，透過微積分和簡單的向量，得到第一個度規張量。

2. 如果不理解相對論所取代的一些物理學，我不知道如何理解相對論。對牛頓力學進行了簡短的討論，並將更多的時間花在了牛頓的萬有重力理論上，我相信這是值得的，其中還包括了如何畫出一顆假想行星圍繞太陽執行的軌域。

3. 討論狹義相對論和閔考斯基時空 的奇異世界，包括反直覺的時間膨脹和長度收縮現象。在利用時空圖的幾何輔助來發展我們的時空知覺之後，我們使用勞侖茲變換 來發展一種更代數的方法。最後，我們來看看狹義相對論是如何重新表述力學定律的。

4. 簡要介紹流形和所有重要的度規張量 g_μν的概念。接下是向量和張量，以便讓我們更容易理解曲率的數學，包括連線系數、向量的平行傳輸、測地線和黎曼曲率張量 。

5. 將這些不同的線索結合在一起，得到 愛因史坦場方程式 。在這個過程中，我們遇到了等效原理 （愛因史坦最高興的想法）、時空測地線和能量動量張量 。

6. 在適當的非相對論條件下，廣義相對論方程式 是如何近似於牛頓力學的公式的。

7. 場方程式的 史瓦西解 ，這是愛因史坦場方程式 的第一個也是最重要的精確解。這個解對緩慢旋轉的物體提供了一個很好的近似，如太陽和地球的重力場。我們推導史瓦西解並利用它來討論廣義相對論的四個經典檢驗。史瓦西解 可以用來預測和描述最簡單型別的黑洞。

8. 對相對論宇宙學的簡要介紹。我們從觀察到的宇宙的四個關鍵內容開始，包括宇宙學原理 ——假設在非常大的尺度上宇宙看起來是一樣的。

羅伯森-沃克度規和弗瑞德曼方程式 共同建立了理論框架，使我們能夠討論幾個簡單的宇宙模型，並對我們自己的宇宙的歷史和演化有了深入的了解。請註意，在相對論中，定義速度c等於1通常會使表達變得更簡單。例如勞侖茲因子 是：

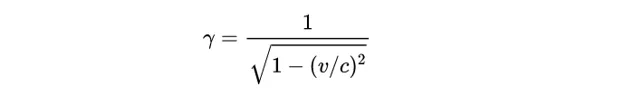
假設c = 1，會變成：

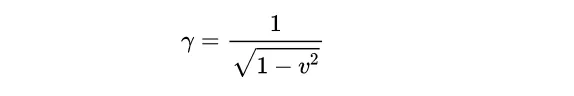
對於學習者來說，這兩個方程式並不明顯意味著相同的東西（它們確實是）。這裏可能會有混淆的地方，因此我盡量在運算式中使用c，而不是1。還要註意，當我們提到「光」時，我們當然不僅僅指肉眼可見的電磁波譜 的狹窄範圍，而是指所有的電磁放射線，如Gamma射線 、x射線、可見光、無線電波等。