力學實驗4:驗證牛頓第二定律實驗的兩大誤差分析
小夥伴們,今天突然想明白了一個道理,或者說想明白了一些事情,人呢,還是要甘於平凡的,但也不用渾渾噩噩,可以不喜歡工作,但要有愛好,像我這樣年紀也不小了,依然愛好寫一些好玩有趣的物理題目分享給小夥伴們,我快樂,你們也快樂,這就夠了,這就是生活了,況且我已經有將近1萬的粉絲了,所以更要繼續努力了。
生活中有些人就很奇怪,比如領導,領導其實也很膚淺的,比如以寫公文為例吧,先不說我寫得好不好,領導的評價永遠是那麽單一,「站位不高」或者「高度不夠」,你看,領導都說不出第二種評價標準,哪怕說一句「狗屁不通」也行呀!每次聽到「不高」我就「煩躁」,說明這就是官話,就是場面話,就是「無話找話」,從而顯得自己「很高」,這樣的評價卻還要讓我來修改,你說氣人不,我怎麽高,「拔苗助長」嗎!
算了,不說了,繼續我的分享吧,至少還有小夥伴喜歡看,哈哈!
關於牛頓第二定理這個實驗,我在「袁野:力學實驗2:探究加速度和力的關系」中有過介紹,今天打算更加詳細的說一說並且有所拓展。
關於這個實驗原理,這裏不再贅述了,重點有二,
1.摩擦誤差:平衡摩擦過度或不夠。
2.受力誤差:就是小車受到的外力並不等於重物的重力,只有當小車品質遠遠大於重物品質時,才可以認為小車受到的拉力等於重物的重力,所以我們應該記住「大車」。
下面,我們仔細分析這兩個誤差,可能產生的結果。
一、研究加速度和受力的關系(小車品質不變)
理想情況,小車受到的拉力為 F=mg ,
則, mg=Ma ( M 不變),
即, a=\frac{mg}{M} (理想情況)
當然,上面顯然屬於理想情況,
下面,我們分析實際情況,
對於摩擦誤差,我們以平衡過度考慮,
對於小車受力,也不再是重物重力,而是按照實際情況分析,
從而得到小車的加速度為,
a=\frac{mg+Mg\sinθ-μMg\cosθ}{M+m} (實際情況)
上面的實際加速度公式中同時包含了受力誤差和摩擦誤差兩個方面。
於是,我們把上式區分成兩個式子,
(1)當摩擦力平衡時, Mg\sinθ-μMg\cosθ=0 ,則,
a=\frac{mg}{M+m} (只考慮受力誤差)
(2)當 M>>m 時,則,
a=\frac{\frac{m}{M}g+g\sinθ-μg\cosθ}{1+\frac{m}{M}}=\frac{m}{M}g+g\sinθ-μg\cosθ (只考慮摩擦(過度)誤差)
做出 a-F(mg) 影像如下,
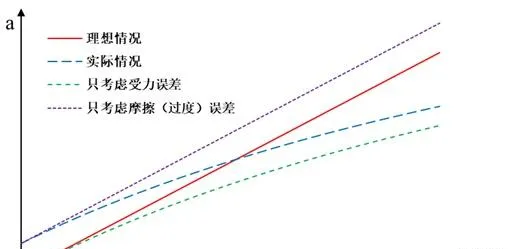
於是,我們發現,對比理想情況,
摩擦(過度)誤差主要體現在與縱座標的截距上,誤差為常數,
受力誤差主要體現在後半段上,因為在後半段 F(mg) 較大,不滿足 M>>m 了,
而反過來說,在前半段則滿足 M>>m ,所以只有摩擦誤差影響。
二、研究加速度和小車品質的關系(小車受力不變)
這時候,mg 保持不變,我們有兩種畫圖的方法,分別是 a-\frac{1}{M} 影像和 \frac{1}{a}-M 影像。
先說a-\frac{1}{M} 影像,
老樣子,寫出理想情況,
a =mg·\frac{1}{M} (理想情況)
下面再寫出實際情況,
a=\frac{mg+Mg\sinθ-μMg\cosθ}{M+m} (實際情況)
實際情況和之前的式子是相同的,只是換了自變量而已。
我們繼續分開考慮,同上面並沒有太大區別,
(1)當摩擦力平衡時, Mg\sinθ-μMg\cosθ=0 ,則,
a=\frac{mg}{M+m} (只考慮受力誤差)
(2)當 M>>m 時,則,
a=\frac{\frac{m}{M}g+g\sinθ-μg\cosθ}{1+\frac{m}{M}}=\frac{m}{M}g+g\sinθ-μg\cosθ (只考慮摩擦(過度)誤差)
作出a-\frac{1}{M} 影像,
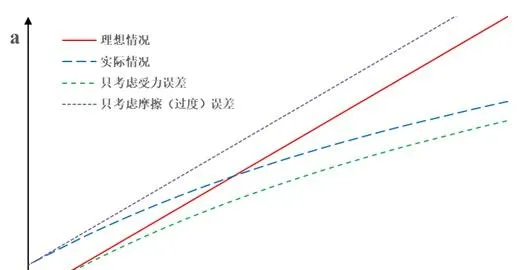
同樣,我們發現,對比理想情況,
摩擦(過度)誤差主要體現在與縱座標的截距上,誤差為常數,
受力誤差主要體現在後半段上,因為在後半段 1/M 較大,即 M 較小,不滿足 M>>m 了,
而反過來說,在前半段,則滿足 M>>m ,所以只有摩擦誤差影響。
然後分析\frac{1}{a}-M 影像時,難度就變大了,或者說有點不一樣了。
我們直接給出式子,
\frac{1}{a}=\frac{1}{mg}·M (理想情況)
\frac{1}{a}=\frac{M+m}{mg+Mg\sinθ-μMg\cosθ} (實際情況)
\frac{1}{a}=\frac{M+m} {mg} (只考慮受力誤差)
\frac{1}{a}=\frac{M}{mg+Mg\sinθ-μMg\cosθ} (只考慮摩擦(過度)誤差)
作出\frac{1}{a}-M 影像,
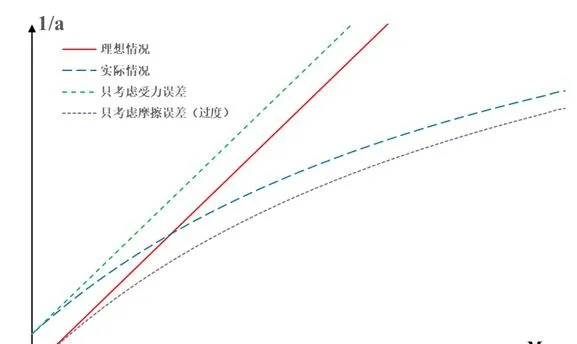
小夥伴們,仔細看上面那個影像,和前面分析的兩種情況是有很大區別的,甚至有點相反的,
對比理想情況,
受力誤差體現在縱軸截距上,無論是否滿足 M>>m ,誤差都是常數,
而摩擦誤差卻體現在了後半段,因為後半段 M>>m ,所以,受力誤差影響較小。
小夥伴們,試著嘗試自己深入思考一下,要有「高度」喲!
我就講這麽多了,「高度」不夠了,哈哈!
最後,送上小禮包一份,祝學業進步,金榜題名!連結:https:// pan.baidu.com/s/1R-YoSi QDz-NaoozVG6jF9Q 提取碼:JN95
對了,近期福利大放送,付費咨詢只需要1元喲!但是不要問太復雜的題目啦,畢竟時間還是很有限的呀!
好了,小夥伴們,咱們下期再見啦!











