推薦一個小工具,可以很方便地計算石墨烯的電導率、介電常數、折射率。
下載連結:https:// opt-simul.com/archives/ 705
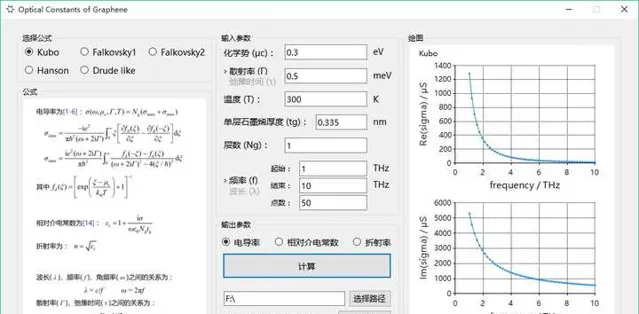
以下是正文:
石墨烯 的電導率、介電常數、折射率等電磁參數主要與頻率 \omega 、化學勢 \mu_{\rm c} 、散射率 \Gamma 、溫度 T 、層數 N_{\rm g} 、單層石墨烯厚度 t_{\rm g} 等因素有關。其電導率可以用 Kubo公式 來計算,然後可以根據電導率進一步計算 介電常數 和 折射率 。
1、Kubo公式
描述石墨烯電導率的Kubo公式由 帶內電導率 \sigma_{\rm intra} 和 帶間電導率 \sigma_{\rm inter} 兩部份組成,總電導率是兩者的和。當石墨烯層數 N_{\rm g} 不大時,總電導率可以寫為 [1] [2] [3] [4] [5] [6] :
\sigma(\omega,\mu_{\rm c},\Gamma,T)=N_{\rm g}(\sigma_{\rm intra}+\sigma_{\rm inter}) (1a)
其中
\sigma_{\rm intra}=\frac{-{\rm i}e^2}{\pi\hbar^2(\omega+2{\rm i} \Gamma)}\int_{0}^{\infty}\xi\left[ \frac{\partial f_d(\xi)}{\partial \xi}-\frac{\partial f_d(-\xi)}{\partial \xi} \right]{\rm d}\xi (1b)
\sigma_{\rm inter}=\frac{{\rm i}e^2(\omega+2{\rm i}\Gamma)}{\pi\hbar^2}\int_{0}^{\infty}\frac{f_d(-\xi)-f_d(\xi)}{(\omega+2{\rm i}\Gamma)^2-4(\xi/\hbar)^2}{\rm d}\xi (1c)
f_{\rm d}(\xi)=\left[ {\rm exp}\left( \frac{\xi-\mu_{\rm c}}{k_{\rm B}T} \right)+1 \right]^{-1} 是 費米狄拉克分布 (1d)
在計算需要註意單位統一:如果角頻率 \omega 的單位取[rad/s],那麽 \Gamma 的單位也必須是[rad/s];如果光子能量 \hbar\omega 的單位取[eV],那麽 \hbar\Gamma 的單位也必須是[eV];在 費米狄拉克分布 中,如果 \mu_{\rm c} 的單位取[eV],那麽 \xi 和 k_{\rm B}T 的單位也必須是[eV]。為了計算方便,建議所有能量單位都取為[eV]。另外還需註意,石墨烯是二維材料,上面Eq.(1)算出來的電導率是 表面電導率 ,單位是[S],而不是[S/m]。
在得到電導率後,利用公式 [7]
\epsilon_{//}=1+\frac{{\rm i}\sigma}{\omega\epsilon_0 N_{\rm g} t_{\rm g}} 和 n_{//}=\sqrt{\epsilon_{//}} (2a)
分別得到石墨烯的 切向相對介電常數 和 切向折射率 ,而石墨烯的 法向相對介電常數 和 法向折射率 都是1,即:
\epsilon_{\bot}=1 和 n_{\bot}=1 (2b)
Kubo公式 對紫外到太赫茲波段都適用,但是我們可以看到 Eq.(1) 還是比較復雜的,要正確計算這些式子並不容易。因此後來人們推匯出一些近似公式來簡化Kubo公式,例如:
2、L. A. Falkovsky近似的第一種公式 [4] [5]
\sigma(\omega,\mu_{\rm c},\Gamma,T)=N_{\rm g}(\sigma_{\rm intra}+\sigma_{\rm inter}) (3a)
其中
\sigma_{\rm intra}=\frac{2{\rm i}e^2 k_{\rm B} T}{\pi \hbar^2 (\omega+2{\rm i}\Gamma)} {\rm ln}\left[ 2 {\rm cosh} \left( \frac{mu_{\rm c}}{2k_{\rm B} T} \right) \right] (3b)
\sigma_{\rm inter}=\frac{e^2}{4\hbar}\left[ G\left( \frac{\hbar\omega}{2} \right)-\frac{\rm i}{2\pi}{\rm ln}\frac{(\hbar\omega+2\mu_{\rm c})^2}{(\hbar\omega-2\mu_{\rm c})^2+(2k_{\rm B}T)^2} \right] (3c)
G(\xi)=\frac{{\rm sinh}[\xi/(k_{\rm B}T)]}{{\rm cosh}[\mu_{\rm c}/(k_{\rm B}T)]+{\rm cosh}[\xi/(k_{\rm B}T)]} (3d)
3、L. A. Falkovsky近似的第二種公式 [5] [8]
也就是將L. A. Falkovsky第一種公式中的 G\left( \hbar\omega/2 \right) 進一步簡化成
G\left( \frac{\hbar\omega}{2} \right)=\frac{1}{2}+\frac{1}{\pi}{\rm arctan}\left( \frac{\hbar\omega-2\mu_{\rm c}}{2k_{\rm B} T} \right) (4)
4、G. W. Hanson近似的公式 [9]
\sigma(\omega,\mu_{\rm c},\Gamma,T)=N_{\rm g}(\sigma_{\rm intra}+\sigma_{\rm inter}) (5a)
其中
\sigma_{\rm intra}=\frac{{\rm i}e^2 k_{\rm B} T}{\pi \hbar^2 (\omega+2{\rm i}\Gamma)} \left[ \frac{mu_{\rm c}}{k_{\rm B}T}+2{\rm ln}\left( 1+{\rm e}^{-\frac{mu_{\rm c}}{k_{\rm B}T}} \right) \right] (5b)
\sigma_{\rm inter}=\frac{{\rm i}e^2}{4\pi\hbar}{\rm ln}\left[ \frac{2|\mu_{\rm c}|-(\omega+2{\rm i}\Gamma)\hbar}{2|\mu_{\rm c}|+(\omega+2{\rm i}\Gamma)\hbar} \right] (5c)
5、Drude-like近似 [10] [11]
\sigma(\omega,\mu_{\rm c},\Gamma,T)=N_{\rm g}\frac{e^2\mu_{\rm c}}{\pi\hbar^2}\frac{\rm i}{\omega+2{\rm i}\Gamma} (6)
這是我算出來的結果與文獻 [12] 中的圖進行對比,兩者符合得非常好:
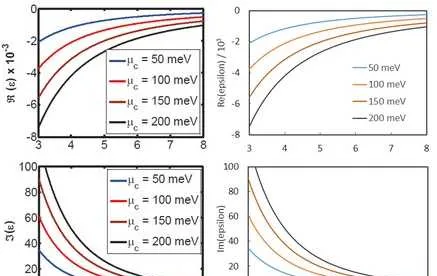
上面5種公式的Matlab計算程式碼 [13] :https:// opt-simul.com/archives/ 691
有需要的朋友還可以從我的主頁下載光學仿真案例(包括COMSOL案例和Lumerical FDTD案例),這些案例都是我原創的,大部份是SCI論文復現:
參考
- ^ V. P. Gusynin, S. G. Sharapov and J. P. Carbotte, J. Phys.: Condens. Matter 19, 026222 (2007). https://doi.org/10.1088/0953-8984/19/2/026222
- ^ V. P. Gusynin, S. G. Sharapov and J. P. Carbotte, Phys. Rev. B 75, 165407 (2007). https://doi.org/10.1103/PhysRevB.75.165407
- ^ L. A. Falkovsky and A. A. Varlamov, Eur. Phys. J. B 56, 281 (2007). https://doi.org/10.1140/epjb/e2007-00142-3
- ^ a b L. A. Falkovsky and S. S. Pershoguba, Phys. Rev. B 76, 153410 (2007). https://doi.org/10.1103/PhysRevB.76.153410
- ^ a b c L. A. Falkovsky, Journal of Physics: Conference Series 129, 012004 (2008). https://doi.org/10.1088/1742-6596/129/1/012004
- ^ G. W. Hanson, J. Appl. Phys. 103, 064302 (2008). https://doi.org/10.1063/1.2891452
- ^ Supporting online material for A. Vakil, N. Engheta, Science 332, 1291 (2011). https://doi.org/10.1126/science.1202691
- ^ Y. Yao, M. A. Kats, P. Genevet, et. al., Nano Lett. 13, 1257 (2013). https://doi.org/10.1021/nl3047943
- ^ G. W. Hanson, J. Appl. Phys. 103, 064302 (2008). https://doi.org/10.1063/1.2891452
- ^ N. M. R. Peres, J. M. B. Lopes dos Santos, and T. Stauber, Phys. Rev. B 76, 073412 (2007). https://doi.org/10.1103/PhysRevB.76.073412
- ^ P. A. D Gonçalves, N. M. R Peres, An introduction to graphene plasmonics (World Scientific Publishing 2016). https://doi.org/10.1142/9948
- ^ R. Alaee, M. Farhat, C. Rockstuhl, et. al., Opt. Express 20, 28017 (2012). https://doi.org/10.1364/OE.20.028017
- ^ 石墨烯光學參數Matlab程式碼 https://www.90pan.com/b2103414











