編輯:編輯部 JHY
【新智元導讀】小模型也能擊敗o1?微軟全華人團隊提出rStar-Math演算法,三大革命性技術突破,不僅讓SLM在數學推理能力上重新整理SOTA,更是擠進了全美20%頂尖高中生榜單。
一夜之間,微軟用小模型(SLM),在數學推理上擊敗o1,沖爆了AI社群熱搜。
不僅如此,SLM在美國數學奧林匹克(AIME)上,拿下了53.3%的亮眼成績,直逼全美20%頂尖高中生!
瞬間,大波Reddit網友線上發出靈魂拷問,「我們將在25年年終前就會有AGI了,不是嗎」?

HugginFace CEO發文,rStar-Math成為HF熱門論文
這篇論文究竟做出了怎樣的技術創新,能讓o1甘拜下風?
論文中,來自微軟亞研院的全華人團隊,提出了全新演算法rStar-Math,證明了SLM無需從高級模型蒸餾,就能在數學推理上,媲美甚至一舉超越o1。

論文連結:https://arxiv.org/pdf/2501.04519
rStar-Math核心在於,讓小模型具備「深度思考」的能力。
團隊借鑒了AlphaGo中蒙地卡羅樹搜尋(MCTS)技術,設計了一個由2個協同工作的SLM組成的系統:
一個數學策略小語言模型(SLM)
一個過程獎勵模型(PRM)
此外,rStar-Math具體設計中,引入了三項技術創新:全新程式碼增強CoT數據合成;全新PRM訓練方法;自我前進演化方案。
透過4輪自我前進演化,並結合數百萬個為747k數學問題合成的解答,rStar-Math讓SLM數學推理能力重新整理SOTA。
在MATH基準測試中,它將Qwen2.5-Math-7B的成績從58.8%提升至90.0%,將Phi3-mini-3.8B的成績從41.4%提升至86.4%,比o1-preview分別高+4.5%和+0.9%。
在美國數學奧林匹克(AIME)上,rStar-Math解決了平均53.3%(8/15)的題目,排名位於高中數學優等生前20%。具體結果如下所示。

Keras之父預言道,2025年將會不斷湧現這樣的研究,透過結合程式搜尋、CoT搜尋,在LLM指導下提升推理基準(包括ARC和數學基準)的表現。
MCTS、遺傳搜尋,你能想到的方法,都會被嘗試。

數學推理難在哪兒?
在測試時計算scaling新範式中,關鍵是訓練一個強大的策略模型來生成有前景的解答步驟,以及一個可靠的獎勵模型來準確評估這些步驟,這兩者都依賴於高品質的訓練數據。
眾所周知,在數學推理中,正確的最終答案並不能確保整個推理過程的正確性。錯誤的中間步驟會顯著降低數據的品質。
然而,策略模型很難區分出來推理步驟到底正確還是錯誤的,從而很難去剔除低品質數據。
與此同時,能夠對中間步驟提供細粒度反饋的獎勵模型,訓練數據更加稀缺:準確的逐步反饋需要大量的人力標註,難以大規模擴充套件,而自動標註由於獎勵分數的雜訊,取得的效果有限。
由於上述問題,現有的訓練策略模型使用基於蒸餾的合成數據,如擴充套件GPT-4蒸餾的CoT數據,但報酬越來越少,無法超越其教師模型的能力;同時,至今為止,訓練可靠的PRM來進行數學推理仍然是一個開放問題。
rStar-Math,三大創新
與依賴更強大的LLM合成數據不同,rStar-Math利用小語言模型(SLM)結合蒙地卡羅樹搜尋(MCTS)建立了自我前進演化過程,叠代生成更高品質的訓練數據。
為了實作自我前進演化,rStar-Math引入了三項關鍵創新。

新CoT數據合成方法
首先,全新程式碼增強型CoT數據合成方法, 將數學問題求解被分解為MCTS中的多步驟生成。在每一步中,作為策略模型的SLM會對候選節點采樣,每個節點生成一個單步的CoT推理和相應的Python程式碼。
為了驗證生成品質,只有那些成功執行Python程式碼的節點會被保留,從而減少中間步驟中的錯誤。
此外,多步MCTS回合會根據每個步驟的貢獻自動分配Q值:那些貢獻更多推理軌跡並導向正確答案的步驟會獲得更高的Q值,並被認為是更高品質的。這確保了SLM生成的推理軌跡由正確且高品質的中間步驟組成。
過程偏好模型
第二,引入了一種新穎的方法,訓練一個作為PPM的SLM,旨在實作所需的PRM,該模型能夠可靠地預測每個數學推理步驟的獎勵標簽。
PPM利用了這樣一個事實:盡管使用廣泛的MCTS回合,Q值仍然不足以精確評分每個推理步驟,但Q值可以可靠地區分正向(正確)步驟和負向(無關/錯誤)步驟。
因此,訓練方法基於Q值為每個步驟構建偏好對,並使用成對排名損失來最佳化PPM對每個推理步驟的評分預測,從而實作可靠的標註。
這種方法避免了傳統方法直接使用Q值作為獎勵標簽,因為這些方法在逐步獎勵分配中固有地存在雜訊和不精確。
自我前進演化
最後,四輪自我前進演化的方案逐步從0構建前沿策略模型和PPM。
研究人員從公開可用的來源中,策劃了一個包含747,000個數學題的數據集。
在每一輪中,使用最新的策略模型和PPM執行MCTS,利用上述兩種方法生成越來越高品質的訓練數據,以訓練更強的策略模型和PPM用於下一輪。
每一輪都實作了逐步的改進:(1)更強的策略SLM,(2)更可靠的PPM,(3)透過PPM增強的MCTS生成更好的推理軌跡,以及(4)改進訓練數據覆蓋範圍,解決更多高難度的甚至是競賽級別的數學問題。
四輪自我前進演化
由於SLM的能力較弱,要進行四輪MCTS深度思考,可以逐步生成更高品質的數據,並透過更多高難度的數學問題來擴充套件訓練集。
每輪都要用MCTS生成逐步驗證的推理軌跡,然後用這些軌跡訓練新的策略SLM和PPM。新模型隨後套用於下一輪,以生成更高品質的訓練數據。
第一輪:啟動初始強策略SLM-r1
為了使SLM能夠自我生成合理的訓練數據,要執行一輪引導訓練,微調初始的強策略模型,記作SLM-r1。
如表2所示,使用DeepSeek-Coder-V2-Instruct(236B)執行MCTS,收集SFT數據。
在這一輪中,由於沒有可用的獎勵模型,因此使用終端引導註釋來標註Q值,並將MCTS的回合數限制為8,以提高效率。對於正確的解答,選擇Q值平均值最高的前兩條軌跡作為SFT數據。

第二輪:訓練可靠的PPM-r2
在這一輪中,使用更新後的7B策略模型SLM-r1,進行大量的MCTS回合以獲取更可靠的Q值標註,並訓練了第一個可靠的獎勵模型PPM-r2。其中,為每個問題執行16輪MCTS回合。生成的逐步驗證推理軌跡在品質和Q值精確度上都有顯著提升。
如表3所示,策略SLM-r2如預期般得到改進;類似的,如表4所示,PPM-r2也比引導輪中的表現更為有效。
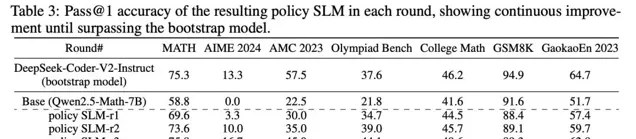

第三輪:使用PPM增強的MCTS顯著提高數據品質
在這一輪中,借助可靠的PPM-r2,要執行PPM增強的MCTS以生成數據,從而生成了明顯更高品質的推理軌跡,這些軌跡覆蓋了訓練集中更多的數學和奧林匹克級問題(表2)。
生成的推理軌跡和自註釋的Q值隨後被用於訓練新的策略SLM-r3和PPM-r3,二者均表現出顯著改進。
第四輪:解決高難度的數學問題
在第三輪之後,盡管基礎學科和MATH問題已達到較高的成功率,但只有62.16%的奧林匹克級問題被納入訓練集。
為了提高覆蓋率,采用了一種簡單的策略:對於16輪MCTS回合後仍未解決的問題,增加執行64輪回合,必要時增至128輪。並對不同隨機種子進行多次MCTS擴充套件。成功將奧林匹克級問題的成功率提高至80.58%。
在經過四輪自我前進演化後,747k數學問題中有90.25%成功被納入訓練集,如表2所示。在剩余的未解決問題中,絕大部份是合成問題。
作者隨機檢查了20個問題樣本,發現其中19個被錯誤標註為錯誤答案。因此,得出結論,剩余未解決的問題品質較低,因此在第4輪結束時終止了自我前進演化過程。
小模型擊敗o1,攻克奧賽級難題
表5展示了rStar-Math與最先進推理模型的比較結果。有三點需要強調:
(1)rStar-Math顯著提升了SLM數學推理能力,達到了與OpenAI o1相當或更佳的效能,同時模型規模大大縮小(1.5B-7B)。
(2)盡管使用了更小的策略模型(1.5B-7B)和獎勵模型(7B),rStar-Math仍顯著超越了最先進的系統2基準模型。rStar-Math持續提升了所有基礎模型的推理準確性,達到最先進的水平。
(3)除了像MATH、GSM8K和AIME這樣的知名基準,rStar-Math還在其他高難度的數學基準測試上表現出了強大的泛化能力,包括奧林匹克數學基準、大學數學和國內的高考數學試題。

擴充套件測試時計算
rStar-Math使用MCTS來增強策略模型,依據PPM引導搜尋解決方案。透過增加測試時的計算量,可以探索更多的軌跡,從而間接地提高效能。
在圖3中,透過比較在四個高難度的數學基準上,不同數量的采樣軌跡下,官方Qwen Best-of-N的準確率,展示了測試時計算擴充套件的影響。
僅采樣一條軌跡時,對應策略LLM的Pass@1準確率,表明模型回退到系統1的推理方式。
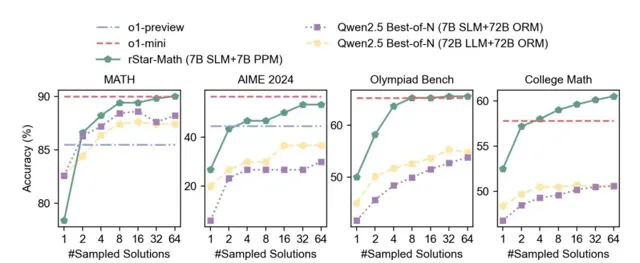
(1)僅使用4個軌跡,rStar-Math顯著優於Best-of-N基準,超過了o1-preview並接近o1-mini。
(2)擴充套件測試時計算在所有基準上均提高了推理準確率,但提升趨勢有所不同。在Math、AIME和Olympiad Bench上,rStar-Math在64個軌跡時表現出趨於飽和或提升緩慢,而在College Math上,效能持續穩步提升。
關鍵發現
內在自我反思能力的出現
OpenAI o1的一個關鍵突破是其內在的自我反思能力。當模型出錯時,它能夠辨識錯誤並透過正確的答案進行自我修正。然而,在開源的大語言模型中,這一能力通常表現得相當不好。
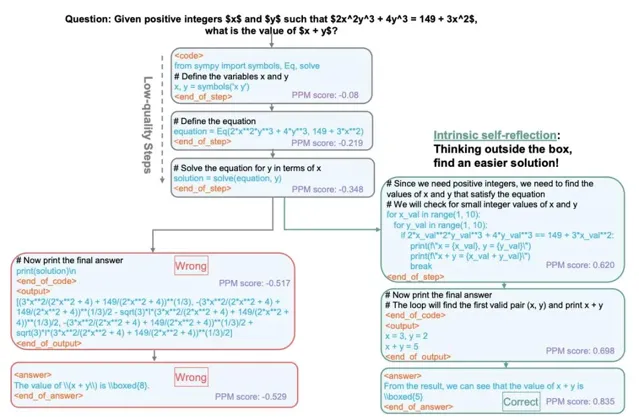
這次意外地觀察到,MCTS驅動深度思考在問題求解過程中表現出自我反思。如圖4所示,模型最初使用SymPy在前三步中形成一個方程式,但會導致錯誤的答案(左分支)。
有趣的是,在第四步(右分支),策略模型意識到其早期步驟的品質較差,並避免繼續沿著最初的問題求解路徑走下去。相反,它回溯並使用一種新的、更簡單的方法解決問題,最終得出正確答案。值得註意的是,並未包含任何自我反思訓練數據或提示,這表明先進的系統2推理能夠促進內在的自我反思。
PPM決定了系統2的推理上限
實驗表明,一旦策略模型的能力達到相對較強水平,決定效能上限的關鍵因素就是過程偏好模型(PPM)。圖5總結了不同規模策略模型的準確性以及獎勵模型帶來的提升。
盡管由於訓練策略、數據集和模型規模的差異,Pass@1準確性存在變化,但足以證明獎勵模型是系統2推理中的主導因素。
PPM辨識定理套用的步驟
在新的實驗中,發現在rStar-Math的問題求解過程中,PPM能夠有效地辨識過程中關鍵的中間步驟。這些步驟透過高獎勵分數進行預測,引導策略模型生成正確的解決方案。

泛化
rStar-Math提供了一種通用的方法,能提升LLM推理能力,適用於各種領域。
首先,rStar-Math可以推廣到難度更高的數學任務,如定理證明。rStar-Math已展示了證明數學命題的潛力。
其次,rStar-Math還能夠推廣到其他領域,如程式碼推理和常識推理。特別是,生成逐步驗證的訓練軌跡需要一個機制來提供反饋,判斷給定的軌跡是否在MCTS回合結束時達到了預期的輸出。
論文也討論了模型消融並在附錄中給出了更多的實驗細節或結果。











