[文末提供原文PDF免費下載(期刊論文版式)]
摘要 :運動規劃是自動駕駛系統中承上啟下的一環,本文綜合分析運動約束型別,並將運動約束轉化為懲罰函式,求解最佳速度的解析解,采用數值仿真手段,生成與最佳路徑耦合的最佳速度曲線,並分析速度曲線的跟隨特性。
01
引言
在前文【 設計搭建汽車機器人 】中詳細闡述了MCR的硬體系統,其中感知系統依賴的傳感器是ZED雙目相機和雷射雷達,獲取機器人周圍環境資訊。
從自動駕駛系統層面分析,環境感知子系統的作用是將機載傳感器獲取的自然環境資訊生成地圖模型,具體可參考【 機器人環境感知研究現狀簡述 】。

圖 1.1 汽車機器人MCR模型
參考【 機器人環境感知研究現狀簡述 】提出的演算法,深入分析道路場景的特點及套用需求,基於MCR平台設計了感知系統,並在【 基於雷射-視覺的環境感知建模方案與套用 】一文中展開了詳細闡述,最後基於該建模方案,生成了簡潔、高效的幾何特征地圖。
【 基於雷射-視覺的環境感知建模方案與套用 】得到的規劃地圖模型包含了道路、障礙物及機器人的資訊,是機器人運動規劃的依據。本系列運動規劃文章將采用路徑-速度解耦規劃框架,綜合分析環境約束、機器人運動約束,從安全適用、即時可靠的角度出發,設計綜合效能強的完整運動規劃模型,如圖 1.2所示,共包含初始路徑規劃及路徑最佳化、速度最佳化和運動控制求解四個子模型,將基於規劃地圖模型直接驅動機器人沿規劃結果軌跡運動。
前文詳細闡述了【 路徑最佳化模型設計 】,本文將在路徑最佳化模型之上主要介紹速度規劃模型設計及建模方法,後續系列文章會綜合闡述運動規劃模型。
(點選或閱讀PDF原文檢視大圖)
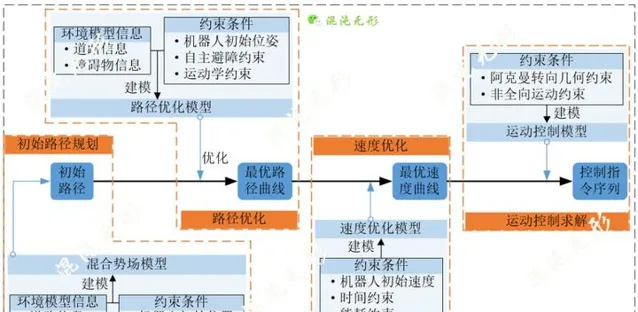
圖 1.2 運動規劃模型流程
軌跡曲線是路徑曲線和相耦合的速度曲線組成的,僅有最佳路徑曲線並不能完整描述機器人運動狀態。故,綜合考慮能耗、目標跟隨等約束,設計速度曲線最佳化模型,基於最佳路徑曲線,生成最佳速度曲線。
02
速度最佳化變量
如圖 2.1(a)所示,機器人從狀態 S rk 變化到 S rk +1,需要滿足非全向約束(僅能做直線或圓弧運動),結合路徑曲線序列(參考【 路徑最佳化演算法設計 】)的曲率,可表示為
式中,[
vsk
,
wsk
]與 [
v
sk
+1,
w
sk
+1]分別表示狀態
S
rk
和
S
rk
+1的線速度、角速度,轉彎曲率
ρ
=1/
r
。
已知初始速度[ v s 1, w s 1],由式(1)知,線速度和角速度求其一即可,因此速度最佳化問題轉化為求解 S rk 變化到 S rk +1的線速度變化量Δ v k,k +1,即Δ v k,k +1是最佳化變量。
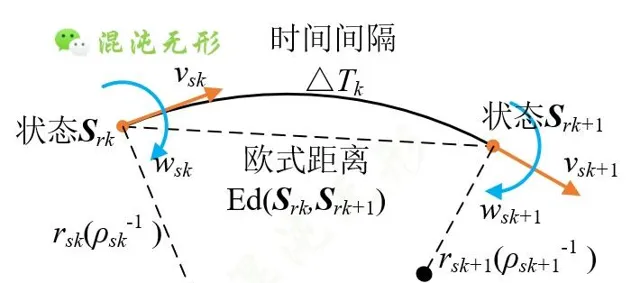
(a)狀態變換圖
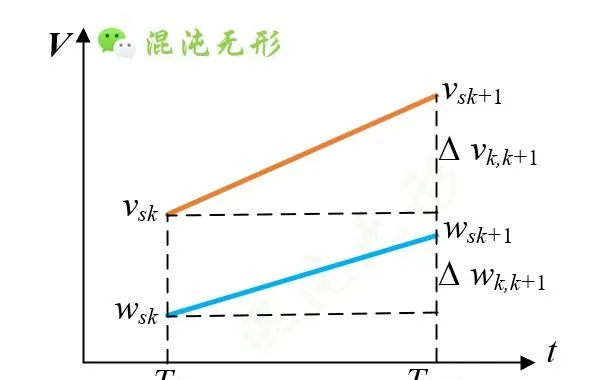
(b)速度變化圖
圖 2.1 運動約束示意圖
03
約束條件
參考圖 3.1,除路徑約束外, State 還需要滿足速度約束。機器人運動需在極限速度範圍[ vmin , vmax ]和加速度範圍[ amin, amax ]內,表示為
式中, vk ( S rk )與 ak ( S rk )分別表示機器人在 S rk 狀態時的運動速度和加速度。
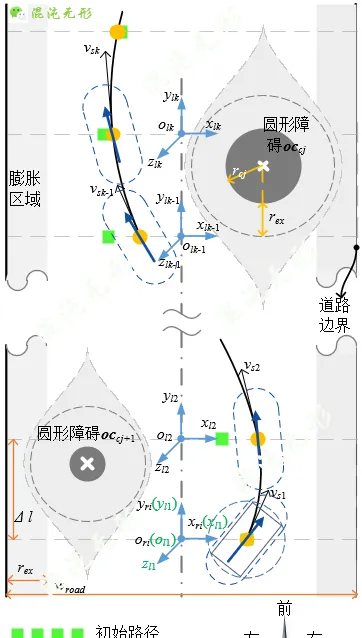
圖 3.1 軌跡規劃及最佳化模型示意圖
除式(2)中的極限約束之外,還需要滿足機器人運動能耗、時耗及目標速度跟隨等要求,具體如下:
3.1
能耗約束
機器人運動可視為平面剛體運動,由動能定理 Ek =( mv )^2/2+( Iw )^2/2,可知速度波動(變化量)越大,則能耗越大,且會降低機器人運動平穩性。因此,機器人能耗可表示為
式中, km 表示速度變化量系數, kI 表示角速度變化量系數,Δ w k,k +1表示狀態 S rk 到 S rk +1的角速度變化量。
結合式(1),得到角速度變化量與速度變化量之間的關系
3.2
時間約束
如圖 2.1,時間間隔Δ Tk 與速度、路程有關,由於相鄰狀態間距小、機器人轉彎半徑大,因此,「以直代曲」估算相鄰狀態的距離,並假設機器人在Δ Tk 內為勻變速運動,因此時間間隔約為
式中, Ed ( S rk , S rk +1)表示相鄰狀態之間的歐式距離。
3.3
目標速度跟隨約束
機器人運動速度是可根據操控者或決策模組調控的,因此,速度曲線需要跟隨目標速度 v tg 的變化,采用速度差值Δ v tg 來衡量跟隨的效果,表示為
04
最佳化目標
4.1
目標函式
速度最佳化屬於多目標最佳化問題,與路徑最佳化的處理方式相似,將速度約束轉化為無約束的綜合懲罰函式,表示為
式中, Jk 表示 S rk 到 S rk +1的速度成本函式,[ λw λv λT λtg ]分別表示各項懲罰項的權重系數;(Δ w k,k +1)^2+(Δ v k,k +1)^2為能耗懲罰項,懲罰速度變化量過大的情況;Δ T k -1為時間懲罰項,懲罰為跟隨速度過快而導致的運動時間變短的情況;(Δ vtg )^2為目標速度跟隨懲罰項,讓機器人運動速度保持在目標速度附近。
最終,最佳化目標轉化為求解綜合成本最低的無約束最佳化模型
式中,Δ v k,k +1*表示相鄰狀態下最佳速度變化量。
4.2
最佳化求解
將公式(3-7)帶入(8)中並化簡, J k 是關於Δ v k,k +1的二次函式,對 J k 求導,得到最小值
根據式(9), v sk +1 =Δ v k,k +1* + vsk ,同時 vsk +1需要滿足約束(2)。本文僅考慮機器人前向運動,因此速度區間為
式中,set( vsk +1)表示狀態 S rk +1的速度可行域, ν ( a )表示加速度限制下的速度大小,表示為
判斷 vsk +1是否在可行速度區間set( vsk +1)中,求解實際最優速度 vsk +1*,具體如下
綜合式(2-12),得到 S rk +1處的實際最優速度 vsk +1*,以及Δ T k 。已知路徑曲線序列(參考【 路徑最佳化演算法設計 】)和 v s 1,可生成最佳速度曲線序列 V:
式中, V sk = [ vsk , wsk ]。最終,結合路徑曲線序列(參考【 路徑最佳化演算法設計 】)和最佳速度曲線序列得到 State ,包含時序的機器人運動狀態序列可表示為
05
最佳化結果分析
圖 5.1(b)中速度曲線及基於圖 5.1(a)中的最優路徑曲線生成的,透過調節目標速度,可調節機器人速度,當目標速度變化的時候,速度曲線立即響應,速度的平穩性決定於加速度設定範圍。而速度曲線沒有完全達到目標速度的原因是速度最佳化包含多種目標,速度跟蹤權重設定到無窮大,則可完全達到目標速度。
(橫螢幕或閱讀PDF原文檢視大圖)
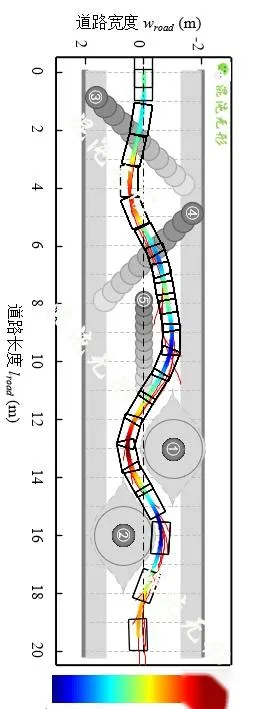
(a)運動規劃狀態圖
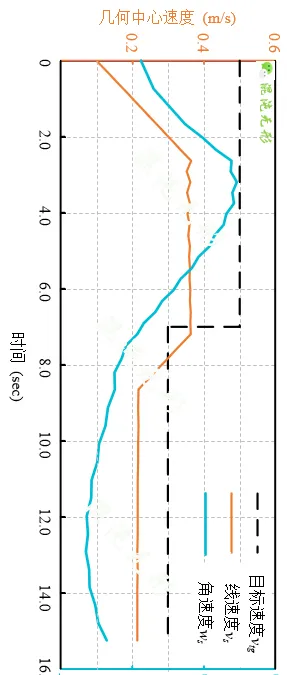
(a)速度最佳化曲線
圖 5.1 直線道路場景運動規劃結果
06
結論與展望
本文綜合分析機器人運動約束,並將運動約束轉化為懲罰函式,求得了最佳速度的解析解,生成了與最佳路徑耦合的最佳速度曲線,分析了速度曲線的跟隨特性,後續會將該速度曲線轉化為機器人運動控制參數,驅動機器人運動,敬請期待。
(文章僅筆者個人分析,有誤請指正,謝謝!)
福利放送
筆者為小夥伴們整理了 期刊論文版式原文PDF ,方便收藏和回味
需 將此文分享到到朋友圈,聯集齊10個贊,截圖發送後台或發送信件:[email protected],稽核透過後,回復下載連結。
註意 :原文PDF效果可參考之前(2022年8月21日)的文章末尾的下載連結,如
Car-like Robot運動模型及套用分析
延伸閱讀
設計搭建汽車機器人(M1)
基於雷射雷達的場景建模演算法分析與套用(M2)
基於視覺的場景建模演算法分析與套用(M3)
基於雷射-視覺的環境感知建模方案與套用(M4)
汽車機器人路徑規劃演算法之混合勢場模型設計(M5)
汽車機器人路徑規劃演算法之初始路徑規劃演算法設計(M6)
汽車機器人路徑規劃演算法之路徑最佳化演算法設計(M7)
機器人運動規劃演算法研究現狀簡述
機器人空間采樣演算法研究現狀簡述
機器人圖規劃演算法研究現狀簡述
機器人環境感知研究現狀簡述
常見移動機器人運動學模型總結
Car-like robot運動參數校準
-----------------------------------------------------------------------------
相關聲明
1.如果轉載本文,文末務必註明:「轉自微信公眾號:混沌無形」
2.若有侵權,請聯系作者


全文完,感謝閱讀!!如果覺得寫的不錯,那就點個贊或者「在看」吧。











