欧拉方程e^(iθ)=cosθ+isinθ是人们公认的优美公式。
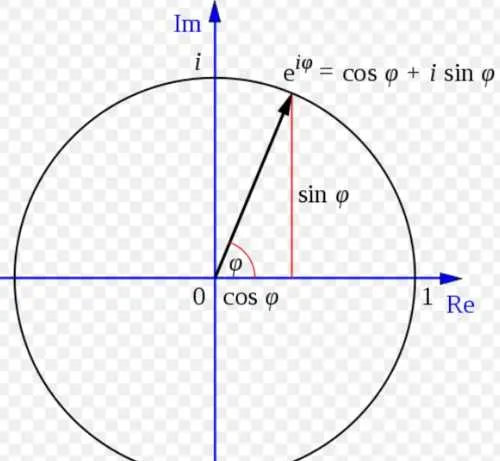
原因是指数函数和三角函数在实数域中几乎没有什么联系,而在复数域中却发现了他们可以相互转化,并被一个非常简单的关系式联系在一起。特别是当θ=π时,欧拉公式便写成了e^(iπ)+1=0,就这个等式将数中最富有特色的五个数0,1,i,e,π,绝妙地联系在一起。

欧拉方程是经济学中的一个重要工具,它描述了个体在面临不确定性的情况下做出经济决策的方式。
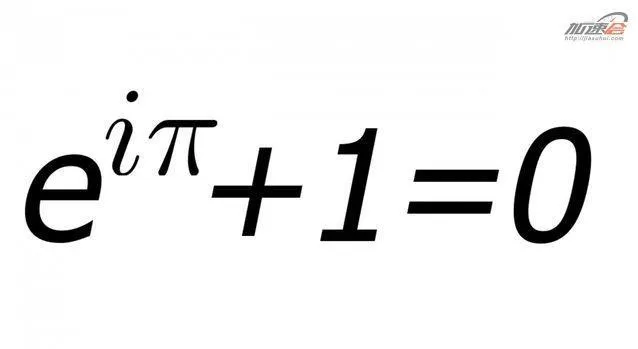
欧拉方程也是经济学中一个非常有用的工具,它可以帮助我们理解个体在面临不确定性的情况下做出经济决策的方式,以及如何使这些决策最优化。
具体的形式为边际收益等于边际成本。这意味着个体会在边际成本等于边际收益的情况下做出最优决策。
欧拉方程可以应用于许多经济学领域,如消费、投资、劳动力等。在消费领域,欧拉方程可以帮助我们理解消费者如何在收入、价格和偏好之间做出最优决策。
在投资领域,欧拉方程可以帮助我们理解投资者如何在不同的风险和回报之间做出最优决策。
在劳动力领域,欧拉方程可以帮助我们理解劳动力供给者如何在工资和休闲之间做出最优决策。
在国际贸易中,欧拉定理可以被应用于解决一些重要的问题。例如,欧拉定理可以帮助经济学家分析国际贸易中的价格歧视问题,即相同的商品在不同的市场上的价格不同。此外,欧拉定理还可以用于解释国际贸易的收益和成本等问题。
在金融学中,欧拉定理可以被用来分析股票市场和证券市场的波动。欧拉定理可以帮助经济学家分析股票价格和证券价格的波动原因,从而得出股票和证券市场的运行规律。此外,欧拉定理还可以被应用于分析股票和证券市场的风险和回报等问题。
欧拉方程还可以与其他经济学工具结合使用,如生产函数、成本函数等。例如,我们可以将欧拉方程与生产函数相结合来解决生产者的生产最优问题。我们也可以将欧拉方程与成本函数相结合来解决企业的投入最优问题。











