不看公式版:
日常的三态变化,就是所谓的一阶相变。其特征就是相态转化过程中呈现出一种不连续性。与此相对应,还有更加复杂的连续相变。一般的热力学描述(如对称性破缺)并不能回答题主的问题。因为这些描述中其实首先预设了气液固三态的存在,然后再用热力学函数来分析三态变化。但是 题主的问题恰恰是我们的预设前提 ,也就是说:
为什么会有气、液、固三种典型状态?而不是
在已知存在气液固三态的前提下,如果解释这三态的区别?首先这里我用平易近人的方式来说一下。
一阶相变的不连续性
其实,气态是一种最容易理解的状态。在气态下,分子距离很远,并且分子运动剧烈。因此分子间的束缚 - 分子间力相对而言就非常弱,可以忽略掉。当我们把分子间力忽略掉的时候,分子就像是一堆相互碰撞的硬球,这就是理想气体。
固态也是一个相对容易理解的状态 - 它是一种有序结构。在这种结构中,每一个分子都找到了与周边分子相互作用势能最低的位置。因而形成了最稳固的状态,这就是晶体。
液态介于其间,相对就复杂得多。简言之,就是因为分子运动足够剧烈,导致总是有些分子不安分地呆在势阱种。分子间的相互束缚总是快速地断开、连接,导致它们相互滑移。但是这些运动又不够剧烈到它们从相互作用之间逃离,变成自由分子。
三态变化中容易理解的是,从气体逐渐降温,它们会渐次经历以上三种状态。但是,不容易解释的是,当我们对气体降温,直至最后结冰,这整个过程中,出现了两次不连续的跳跃。这两次跳跃就把状态分成了三个截然不同的聚集状态。所以关键的问题是:
这种不连续性是如何产生的?在不连续跳跃的时候,为何会有两种不同的聚集状态并存?
我们用水来做例子说明这个情况。我们想象有一个系统,是一箱水蒸气。现在我们开始向外抽取热量。随着热量的向外传递,蒸汽的温度不断降低,体积不断缩小。达到沸点的时候,温度则不再降低,这时候液态水就形成了。此时两种聚集状态同时出现,中间有明显界面。
也就是说,这是一种不连续的变化:水蒸气并不是一直连续降温,体积一直连续缩小的。它会在某个温度(沸点)突然发生了阶跃式的变化:体积突然大幅收缩,热力学性质突然发生跳变。而这种变化就对应着液态水的生成。这种突发的不连续性,就把水的状态分割成气液两态了。
同理,当我们继续降温,就会又出现一个不连续的变化。这个不连续性,就把水的状态分割成液固两态了。
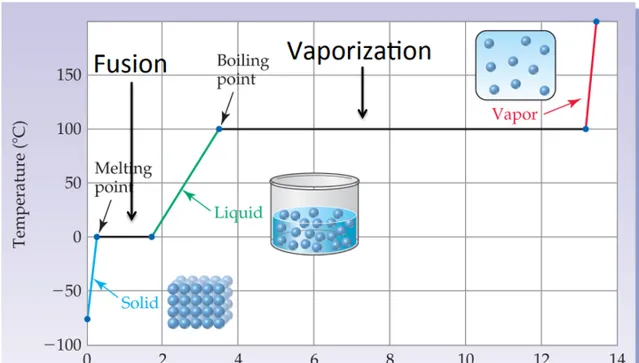
我们不妨来开一下脑洞:我们来假想一下,如果在降温过程中,蒸汽可以连续地变成水,然后连续地变成冰。也就是说,随着降温,蒸汽体积不断缩小,密度不断增加,然后渐渐地变成了水(不存在两相并存的过程)。然后随着持续降温,水渐渐地粘稠,变成果冻状态,然后果冻渐渐变硬,最终变成冰。
在这种假想的情况下,我们会觉得水只有一种相态。他只不过是密度和「硬度」的连续变化而已。
现在,正是因为在过程中出现了两次不连续过渡,才让我们产生了「气液固是截然分立的相态」这种概念。
相的稳定性
那么,为何会有这种不连续变化呢?这是 热力学失稳结果 。也就是说,当蒸汽降温、收缩的过程中,会在特定的时候进入到一种 不稳定的过渡状态 中,这种过渡状态无法稳定存在,会自发崩解为两个稳定的相态。
我们这里先说一下关于热力学稳定性的结论:
一个热力学状态的稳定性条件是,它的比热必须大于零,或者说它的膨胀率必须大于零。
这里稍加说明。为何有这种条件。有兴趣的话,可以看后面严格的热力学推导。
比如说, 如果一个系统的比热小于零。那么会发生什么呢?
如果系统比热小于零,意味着当它向外散失热量时,它的温度上升,反之如果它吸收热量,则温度下降。我们想象一个孤立系统,它无时无刻面临着内部的涨落 - 当然,这些涨落的波动非常小。在一个小局部,突然产生了一个小的波动,使得它的产生了一点向外的净能量流动。那么:
- 由于负比热的存在,导致它的温度上升。而同时,它的周边会接收到传入的热量,因而同样道理导致周边的温度下降。
- 这样一来,就会形成一个温差。
- 这种温差会加速这个局部向外的热量流动。
- 因此,这会进一步导致该局部的温升和周边的温降,进而加大温差。
- 从而加剧热量传递……。
这就形成了一个 正反馈 。导致系统平衡的崩溃。这个局部的温度迅速上升,而周边则温度迅速下降。
同理, 如果一个系统的膨胀率小于零,那么会发生什么呢?
一个负的膨胀率意味着,当系统的压力增加的时候,它的体积将会膨胀;压力减小的时候,体积缩小。那么,当系统中产生一个小波动,那么:
- 局部压力增加,体积膨胀。
- 体积膨胀导致其压缩周边的体积,周边体积缩小,因此压力缩小。
- 这样一来,该局部压力增加,周边压力降低,就形成了压力不平衡。
- 这种压力不平衡导致这个局部继续膨胀,压力继续增加。
- 因而周边体积继续缩小,压力继续降低。
- 因此,压力不平衡加剧。
- ……
这就形成了一个 正反馈 。导致系统平衡的崩溃。这个局部的压力迅速上升,而周边则压力迅速下降。
气液相变
那么,这种稳定性条件又和相态变化有何关系呢?
答案是, 从气态到液态的变化过程中,中间的过渡状态是不稳定的。因此气体会直接跳过这种过渡状态变成液体。
从气体向液体过渡的过程中,理论上的确存在一个连续的过渡状态。但是,这种过渡状态有负热容或负膨胀率。
这个负热容是怎么来的呢?我们可以从分子间力说起。 分子间力是一种短程力 ,它随着距离迅速衰减,只有当分子十分靠近的时候,才会发生作用。
气体状态下分子间力可以忽略,但是当分子间距离足够接近、且运动比较温和的时候(温度较低时),它们之间的吸引力就不可忽略了。而负热容和负膨胀率的性质就是由分子间力引起的。
我们先来看看这里的负膨胀率是如何起作用的。具体讲,在此时,如果系统的局部发生一个波动,导致该处分子间隙变小,会发生什么呢?很显然,
而同时,该局部的周边会发生反向的正反馈:
这就是 负膨胀率 的影响。
我们也可以换一个角度,从 负热容 的角度来说这件事。当系统向外放热的时候,体积缩小。由于分子引力的作用,导致它的势能下降。势能的下降就会使得分子动能上升。因此它的温度反而上升。温度上升导致它放热更快,这也是一个正反馈。我们前面看到,这是一种不稳定的状态。因此,这种过渡状态无法存在,它会迅速崩解为稳定的液态和气态,成为两相并存的状态。这就是 负热容 的影响。
也就是说,当分子间吸引力开始起作用的时候,理想气体的那种自由分子的状态就被打破了,它变得不稳定,要么倒向气态,要么倒向液态,而不可能稳定地存在于气液的过渡态。因此,只有两相并存的状态,而没有两相过渡的状态(特殊情况下会存在,但是极不稳定)。
这个过程和 黑洞的形成 原理其实是类似的。在自引力系统中,一个系统的熵最大状态不是均匀分布的状态。这就是为何星云会聚集变成恒星。分子间力显然和万有引力完全不同,这种不同体现在分子间力是一种短程力。比如说典型的London力是距离的六次方反比的。因而普通的均匀气体是一种稳定的状态 - 当分子间距离足够远,分子间力几乎为零。而自引力系统中,万有引力是距离的平方反比的,所以万有引力是一种长程力,因而星云就会收缩。
只有当气体体积足够小,小到分子间力不再可以忽略时,此时分子间力才成了系统不稳定的源泉。
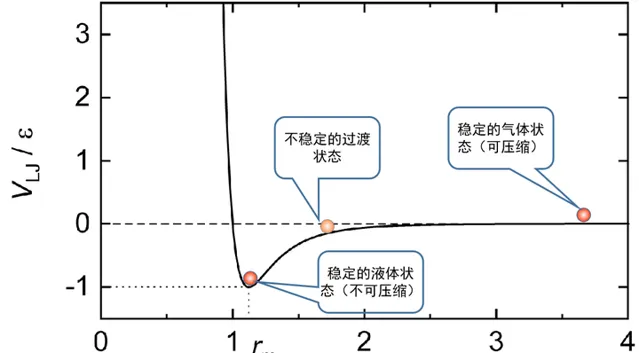
但是,气液两相之间的转换,并不一定会发生这种失稳现象,也就不一定会出现不连续的跃变。在超临界状态下,这种变化就是连续的(这就是下文小刚老师的答案中所说的气液是一相的原因。这个说法不能说错,但是太潦草了,对没有接触过相变理论的人非常容易误导)。 在超临界的情况下,由于温度和压力都很高,分子间的碰撞就会一直占据主导作用,而分子间的吸引力就不再重要,因此绕过临界点从气体过渡到液态是没有不稳定的过渡态出现的,因此也就没有相变过程。
液相的稳定存在
上述不稳定的气液过渡的状态中,由于 分子间吸引力的存在导致分子聚集状态直接决定了势能的变化,导致了负热容/负膨胀率的产生。 那么,势能最低的状态是什么呢?显然,是晶体结构。从气体的自由分子,到分子开始聚集,再到最终晶体的形成之间,就会一直伴随着分子势能的下降。直至最稳定的晶体结构。这就出现了一个问题:
分子的聚集态在气体和液态之间,为何会出现一个稳定的液相(在液相中分子势能不变),而不是从气态直接过渡到固态呢?
一言简化之,就是液态和固态之间的对称性是不同的。但是这个情况会比较复杂。
从液态到固态的变化,其密度不会发生显著变化。也就是说,分子间距的变化很有限。但是一个最大的变化就是,从分子间相对自由的流动变成了 长程的稳固有序排列 。从宏观上说,就是固体的 剪切模量不再是零 。F. A. Lindemann上世纪初的模型中,假定分子的振动幅度达到分子间距的一定比例时,固体的稳定性就失去了,因此它就开始融化。融化所吸收的热量于是就保持了固态中的分子振动不会继续增大。这个模型很简单,也很有用。但是它并没有回答这样一个问题:
液相到底是一种什么样的稳定状态呢?
固态是一个相对容易理解的状态 - 它是一种有序结构,势能最低的状态。在这种状态下,分子间相互作用力最强,分子的位置就被稳固地束缚起来。但是液态是一种分子间力相对较强,但是有不足以使其形成稳固排列的状态,情况就非常复杂。可以说直至现在为止,令人满意的普适理论还没有出现。因为这个过程中太复杂了,这和具体的 分子构型、分子间相互作用的形式、晶形结构、内部缺陷、表面性质 等一系列复杂问题都息息相关。从液态到固态的变化,单纯从单个的分子间的相互作用是不容易解释的,必须要从 大量分子的长程结构 入手 - 因为固体和液体的最大区别就在于长程的有序结构。
气液态的区别情况可以简单地用下图表示 [1]

因此,固相的形成不是单一的分子之间的相互作用,而是大量分子的协同作用,在这个过程中,某个局部的热运动涨落就可以轻易地把周边的有序结构给打破了,而这种局部有序结构的丧失就会像多米诺骨牌一样引发全局的崩溃。这就使得固相的形成难度比液相更高 - 它需要把热运动的影响降低到更低的水准。
还是以水为例,像水这种分子极性高并且相互作用复杂的物质,聚集形态会非常复杂。水中的氢键存在非常普遍,而氢键的形成与分子的形状、位置、取向息息相关。当每个分子都以最多氢键的方式和其他分子结合时,水分子以规则的方式排列,这就是晶体 - 冰。因为氢键的强度远高于一般的分子间力,这种方式的排列,就是势能最低的情况。
但是在温度比较高的时候,这种规则排列无法达成,因为水分子不断振动,打破这些氢键。水分子间的 氢键就一直在不断地打破并且不断地重建过程中 ,这个过程是以飞秒计的。有人说,整体看来在液态水中,大约有12%的氢键处于被打破的状态 [2] 。就是因为这12%的氢键断裂,使得水的整体规整结构被破坏了。 长程的聚集难以持续,但是短程的聚集却是很容易的 。在液体中,分子间的复杂相互起作用,使得分子会三三两两地聚集成团,不断发生「滑移」。由于分子的不断碰撞,这些分子团会呈现出聚集-打散-重新聚集的过程。于是乎形成了流动的状态。 [3]
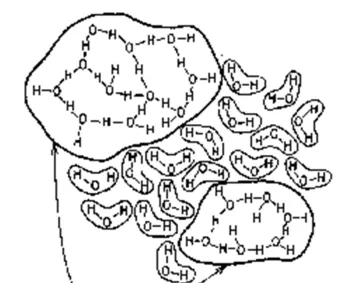
一般说来,液态水中的水分子大约聚集数量在20~200个之间 [4] 。这种局部结构,有规整的,和冰的晶型结构类似,也有不规则的。从某种程度上说,水中的结构在很大程度上和冰没有本质区别,所差的,只是能否形成长程结构
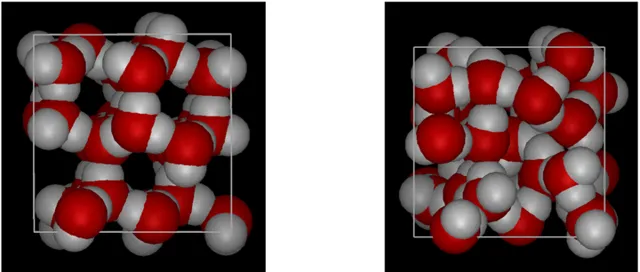
比如说,一种推测的规整分子团的结构是280个水分子的聚集 [5] 。

所以说,人们对固液相变的理解,并不像气液相变那么清楚。这里我仍然定性地用描述一下我的个人理解。
前面提到, 分子间相互作用是一种短程力 。当在液体中,很多分子聚集成团的时候,分子团的尺寸就会比单个分子大得多。相对而言,分子间力就更不容易发生作用。直观讲,较大的分子团接近的时候,其接触点相比于单个分子要小得多。比如说像上面的水分子团的结构,一个 \left( H_2O \right)_{280} 的分子团所能提供的氢键点位要远少于280个单个的水分子。因此,一旦分子聚集成团,那么分子间力的影响就显著下降。
我们前面提到,分子间的相互作用力在气液相变过程中起到了关键作用。它的存在导致气体向液态过渡的过程中出现了状态失稳的现象,从而导致了不连续的变化(相变)。而在达到液态的时候,由于分子间作用力的影响,分子局部聚集,从而导致分子间作用力的影响力下降,就导致了它不再继续聚集,而保持了一段时间的连续变化,这就是稳定的液相的存在。
液固相变
对液态水来说,随着温度的继续降低,分子间作用力的影响又会缓步增加。随着分子间力的影响增加,分子团之间就会越来越出现互相吸引从而更加聚集的情况。此时,类似前述气液相变中的不稳定过渡态就又会出现了。
比如说在某个局部,因为一个扰动,分子的聚集程度突然增加了,那么:
而相反地,这个局部的大规模聚集就必然导致周边分子聚集程度被打破,同时,由于上述的大规模聚集导致的势能下降,必然使得周边分子运动更加剧烈。那么在周边:
我们可以看到,前述的大尺度有序结构的形成伴随着势能的下降。这就类似气液过渡态的那种负热容的情况:当向外传递热量的时候,长程的有序结构形成,从而导致势能显著降低。而势能的降低则会导致动能的增加,使得温度增加。于是这种过渡态就会崩解为稳定的固态和液态。形成两相并存的不连续过程。
请注意这是一个非常定性地、简化地说法。这中间 表面性质 以及 缺陷的性质 起到了极其重要的作用,但是这里就忽略了。
空间熵和动量熵
从热力学第二定律的角度,液态结冰的过程可以这样来看,这是一个是以 空间熵换取动量熵的过程 。
我们可以简单地将熵归结为相空间的体积的对数。也就是说,一个系统的熵,取决于两个方面:它在位置空间中的自由度,以及在动量空间中的自由度。
很显然,液态在位置空间中的自由度要大于固态。因为液态分子虽然受到束缚,还是可以在较大的空间中移动,而不是只在晶格附近振动。所以说液态有着较高的熵。
随着温度的降低,分子的热运动降低,它的动量空间自由度就会随之下降。也就是说,它的运动的速度分布变窄了。
固态有着更低的势能,可以换来更高的动能,进而得到更大的动量自由度。而同时它却有着更低的位置自由的。总的熵就受到这两种相反趋势的支配。当温度较高的时候,系统选择更大的位置自由度,从而达成更高的总熵。而当温度较低的时候,分子已经非常拥挤了, 此时位置自由度的贡献降低,而动量自由度的贡献相对更高 。达到一定的低温后,一部分分子就会自发放弃位置自由度,选择更加规则的空间排布,释放出能量来保持另一部分的温度不再持续下降,从而使得动量自由度维持在较高的水平,换得更高的总熵。从宏观上看,就表现为一部分液体结冰,从而维持系统的温度不再下降。在这个过程中,熵减是由位置自由度的压缩完成的。
假使在降温的时候液体不结冰,那么温度会持续降低,那么系统的动量自由度会持续下降 - 因而它对总熵的贡献持续下降。而此时由于分子相对已经很拥挤了,所以位置自由度也不会很高。宏观上,这就是一种上面脑洞中提到的「果冻」类似的过渡态。这种过渡态比起两相并存(即牺牲位置自由度换来动量自由度)的熵更低,所以它会自发地变为两相并存。
如果你对朗道相变理论很熟悉,这种情况就是相变过程中的鞍点情形。从自由能上看,就是随着系统有序度(coorelation length)的变化,存在 两个稳定态和一个亚稳态 。
这种情况可以用一个日常生活的例子来说明。比如说我们有一个正方形的盒子,里面放置着几根牙签。我们晃动盒子,会发现牙签的排列非常杂乱。这是一种典型的熵增。但是当我们放置一把牙签进去,然后再晃动盒子,我们会发现原来杂乱的牙签会整齐地排列起来。这看起来变得更加有序了。这是自发熵减了吗?不是的,因为牙签的整齐排列,会使得牙签的运动更加自由。所以它的取向虽然更有序了,却换来了运动的更大杂乱。
综上所述,三个典型相态的形成就是这样的:
自由分子(气体)\xRightarrow{稳定性丧失} 束缚分子(液态)\xRightarrow{稳定性丧失} 长程有序束缚分子(固态)
补充公式版:相变的一般热力学描述
从热力学上讲,自由能最低的状态是最稳定的存在状态。从吉布斯方程看:
dG=Vdp-SdT
在等压过程种,由于熵总是正值,所以自由能总是随着温度的增加而减小。并且,由于
S_g>S_l>S_s
所以定性看,气液固的自由能随温度的变化如下:
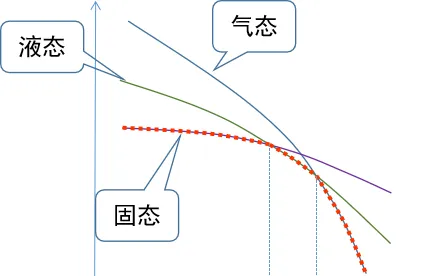
因此随着温度的降低,物态就会从气态变成液态再变成固态。当气液自由能相等的时候,就是沸点,液固自由能相等的时候,就是熔点。
由于
G=H-TS
所以,由于两个相态之间的熵值不连续,则必然会出现相变过程中的不连续,表现为潜热的存在、密度的变化等。
补充公式2:典型的稳定性判据
这里我们推导一下相态的稳定性判据。
对一个孤立系统,在一个平衡态,我们有:
S=S_{eq}
这个平衡态必须有两个特征,第一,它的熵最大,第二,它是稳定的。
熵最大这个很容易理解,因为这是热力学第二定律的直接结论。它是稳定的,意味着对任何扰动,它是负反馈的,也就是说,它会自发地返回到平衡态。
我们假设一个系统。这个系统中一个局部发生了一点点扰动(比如说温度变化了一个 \delta T ),那么这点扰动会引起系统如何变化呢?
我们把这个系统分成两个子系统:发生扰动的那个小局部为子系统1,剩余的为子系统2。那么我们有:
S=S_1+S_2
对于这个扰动,我们可以计算它带来的熵变:
\Delta S=S-S_{eq}=\left( \frac{\partial S_1}{\partial U_1} \right)\delta U_1+\left( \frac{\partial S_2}{\partial U_2} \right)\delta U_2+\left( \frac{\partial^2 S_1}{\partial U_1^2} \right)\frac{\left( \delta U_1 \right)^2}{2}+\left( \frac{\partial^2 S_2}{\partial U_2^2} \right)\frac{\left( \delta U_2 \right)^2}{2}+...
由热力学基本公式我们知道
\left( \frac{\partial S}{\partial U} \right)=\frac{1}{T}
所以:
\Delta S=\left( \frac{1}{T_1}-\frac{1}{T_2} \right)\delta U+\left( \frac{\partial}{\partial U_1}\frac{1}{T_1}+\frac{\partial}{\partial U_2}\frac{1}{T_2} \right)\frac{\delta U^2}{2}
请注意,上式中用到了孤立系统能量守恒的条件,也就是:
\delta U_1=-\delta U_2\equiv\delta U
由于 \delta T 为无穷小量,所以上式中第一项为零。而对于第二项中,我们有:
\frac{\partial}{\partial U}\frac{1}{T}=-\frac{1}{T^2}\frac{\partial T}{\partial U}=-\frac{1}{T^2}\frac{1}{C_V}
所以,第二项就变成了:
\frac{1}{2}\delta^2S=-\frac{C_{V1}}{2T^2}\left( 1+\frac{C_{V1}}{C_{V2}} \right)\left( \delta T \right)^2
由于子系统1远远小于子系统2,所以,
\frac{1}{2}\delta^2S=-\frac{C_{V1}}{2T^2}\left( \delta T \right)^2
由于平衡态中熵处于最大值,所以,任何的扰动都只能使得熵减少。因而,我们有:
\delta^2S=-\frac{C_{V1}}{T^2}\left( \delta T \right)^2<0
因此,我们得到了 相态稳定的条件,就是它的比热必须大于零 。
同理,我们可以假设一个压力的扰动,这样我们会得到另外一个条件:
\delta^2S=-\frac{1}{TV k_T}\left( \delta V \right)^2<0
也就是说, 相态稳定的另一个条件就是,它的压缩率必须大于零。
参考
- ^ doi:10.1063/1.4818747
- ^ Cho et al 1997, Suresh et al 2000
- ^ https://doi.org/10.1039/DF9572400133
- ^ Turi et al. Science 2005
- ^ Martin Chaplin 2000











