Batch Normalization

实现有多简单,标准化+反标准化。
理论有多复杂,到目前为止,都没有很好的理论证明,绝大多数文章还停留在实验阶段。
据我所知,BN的解释经历了这么几个主要阶段:
- 避免Internal Covariate Shift
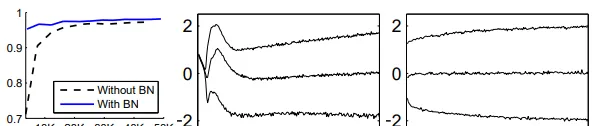
原始的BN论文给出的解释是BN可以解决神经网络训练过程中的ICS(Internal Covariate Shift)问题,所谓ICS问题,指的是由于深度网络由很多隐层构成,在训练过程中由于底层网络参数不断变化,导致上层隐层神经元激活值的分布逐渐发生很大的变化和偏移,而这非常不利于有效稳定地训练神经网络。
2. 平滑loss landscape
BN效果好是因为BN的存在会引入mini-batch内其他样本的信息,就会导致预测一个独立样本时,其他样本信息相当于正则项,使得loss曲面变得更加平滑,更容易找到最优解。相当于一次独立样本预测可以看多个样本,学到的特征泛化性更强,更加general。
这个结论在之前的How Does Batch Normalization Help Optimization?文章中明确提出来过。
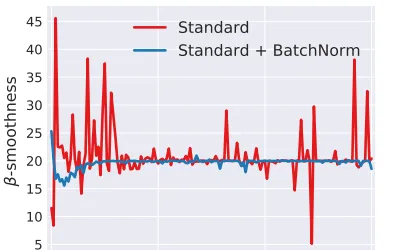
图中展示了用L-Lipschitz函数来衡量采用和不采用BN进行神经网络训练时两者的区别,可以看出未采用BN的训练过程中,L值波动幅度很大,而采用了BN后的训练过程L值相对比较稳定且值也比较小,尤其是在训练的初期,这个差别更明显。这证明了BN通过参数重整确实起到了平滑损失曲面及梯度的作用。
3. 导致Information Leakage
在最近很火的对比学习中,如果在mini-batch内计算BN统计量,就会导致预测一个独立样本时,会引入其他mini-batch样本的信息,造成信息泄露,骗过模型。
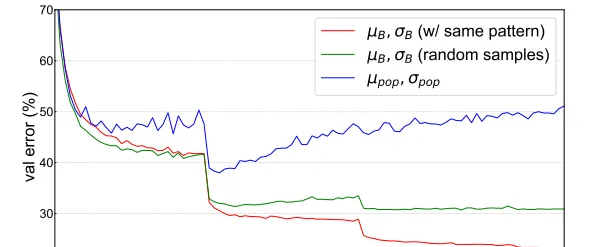
如图所示,当使用random采样的mini-batch统计量时,验证误差会增加,当使用population统计量时,验证误差会随着epoch的增加逐渐增大,导致明显的过拟合,验证了BN信息泄露问题的存在。
即便是在理论如此匮乏的情况下,BN也孕育出了许许多多的变体,比如GN、LN、IN等等。
batch normalization可以说是深度学习时代的black art,或者说是necessary evil。
Reference
[1] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
[2] How Does Batch Normalization Help Optimization?
[3] Rethinking "Batch" in BatchNorm











