题主提到了矩形,估计是想问积分的时候的矩形高度取值、以及误差为什么会消失。
先两句话回答题主的问题:
第一问:
问:矩形的高选取多少?一句话回答:矩形的高度可以在它所在的区间内 \small y 的最大值和最小值之间任意选择,因为随着区间划分越来越细,最终误差总是会消掉。
于是第二个问题就来了:我们怎么知道误差一定会消掉?
第二问:
为什么不怕无限多个误差之和为大误差?一句话回答:简单地说,这正是因为积分可以看作 求面积 ,所以用「细矩形」进行逼近时,产生的误差也就是 面积的误差 ,由于面积包含了 平方 运算,因此这个误差对应的是区间长度的 二阶 无穷小,对每个二阶无穷小进行 一阶 的无穷多次求和后,得到的仍然是一阶无穷小,再取极限就归为零了。
接下来具体说说一句话扯不清楚的细节。
为安全起见,我们只考虑正常积分,即积分区间为有限区间,且区间内没有奇怪的发散点,并且满足黎曼可积条件( 根据巨佬RD的回答补充此条…… )。
假设积分区间长度为 \small L ,将这个区间分为 \small n 等分,则每个小区间的宽度为:
\small \Delta L=\frac{L}{n}
对于第 \small i 个小区间、即 \small \left(x_{i-1},x_{i}\right) 上的矩形,我们先假设其高度为 \small y_{\min,i} ,如下图:
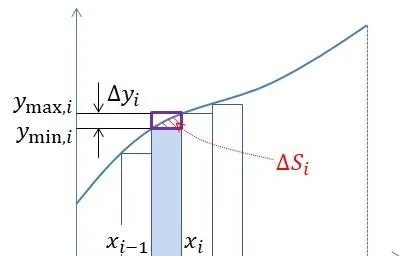
可以看出,图中红色阴影部分面积面积 \small \Delta S_i 就是小区间上的真实积分值与矩形面积之间的误差。我们还可以看出,这个误差是 小于图中紫色边框的小矩形面积的 。
另外,不难想象,只要矩形高度在 \small y_{\max,i} 和 \small \small y_{\min,i} 之间取值,那么表示误差的面积 \small \Delta S_i 总是小于紫色边框的那个小矩形 。
而紫色小矩形的面积为 \small \Delta L\Delta y_i ( 也就是 \small \Delta L\left( y_{\max,i}- y_{\min,i}\right) )
于是第 \small i 个小区间上的误差为:
\small \Delta S_i\leq\Delta L\Delta y_i=k_{i}\Delta L^2
其中 \small k_i=\frac{\Delta y_i}{\Delta L}=\frac{y_{\max,i}- y_{\min,i}}{\Delta L} 为紫色矩形对角线的斜率
( 上面图中画的是函数在小区间内单调递增的情形,但即使函数在小区间内不是单调的,上述关系也成立,题主可以自己画图看一看 )
于是整个积分区间上的总误差为:
\small \Delta S=\sum_{i=1}^n\Delta S_i\leq\Delta L^2\sum_{i=1}^n k_i
我们假设所有的斜率 \small \left\{k_i\right\} 中最大的为 \small K ,则:
\small \sum_{i=1}^n k_i\leq nK
于是:
\small \begin{align} \Delta S&\leq\Delta L^2\sum_{i=1}^n k_i\\ &\leq\Delta L^2nK\\ &=\frac{L^2}{n^2}nK\\ &=\frac{L^2K}{n} \end{align}
对于积分区间有限、且没有发散点的正常积分, \small L,K 都是有限值,那么随着 \small n\rightarrow \infty , \small \Delta S 自然就趋于0了
所以最后误差一定会被消掉。











