@看风景的蜗牛君 的回答从几何方面来论证了不太可能看到昨天的影像。我下面就从能量的角度来进行论证,说明从能量的角度来看也是不太可能的。
当光垂直照射到物质上时,几乎不可能是百分百反射的。因为光会不可避免地与物质发生相互作用。比如物质中的电子会被光激发到较高的能级,随后可能以热辐射的形式回到基态,从而导致损失等等。
金属镜子的反射率可以用 Hagen–Rubens 关系来大致描述 [1] :(没有本征吸收的情况下)
R\approx1-2\sqrt{\frac{2\epsilon_0\omega}{\sigma}}=1-4\sqrt{\frac{\pi\epsilon_0\nu}{\sigma}}
其中 R 是反射率, \omega 是入射光圆频率, \nu 是入射光频率, \epsilon_0 是真空电容率为 8.85\times10^{-12}\ \rm F⋅m^{-1} , \sigma 是金属的电导率
已知导电率最好的金属是银 [2]
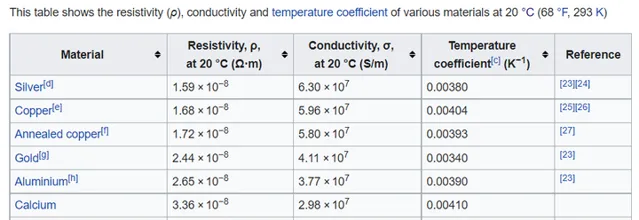
那么我们可以计算出780 nm时(可见光范围内频率最小,为 3.85\times10^{14}\ \rm Hz )银的理想反射率大约为 95%
实际的银镜反射率比计算值略好,可以达到99%。比如下图是来自于Thorlabs的数据。
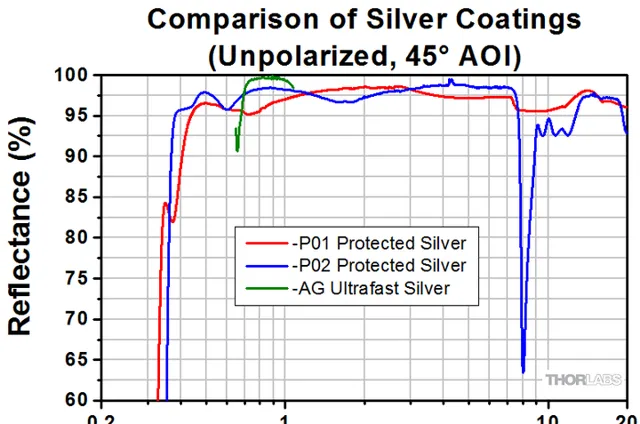
而一些特殊的dielectric mirror,其反射率甚至最高可以达到99.999%! [3] 下面我将会论述,哪怕反射率突破目前的极限达到了6个9,也会因为能量损失而无法提供能看到昨天的能量的。
假如两个镜子之间的距离是10米(距离增加将会不利于几何关系,距离减小将会不利于能量关系,在此取10米)
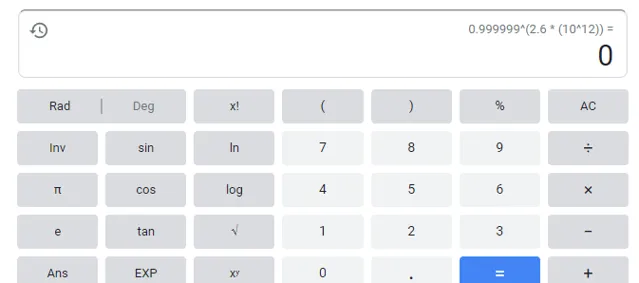
那么24小时前的光已经反射了 \frac{c*t}{d}=\frac{3\times10^8\times3600\times24}{10}=2.6\times10^{12} 次
假设反射率高达99.9999%,那么经过 2.6\times10^{12} 次反射后,剩下的能量为…… 额,谷歌计算器精度不够算不出来。。。(可以有人教我这里如何估算么?我只知道因此次数过高,没法简单用泰勒展开计算。)
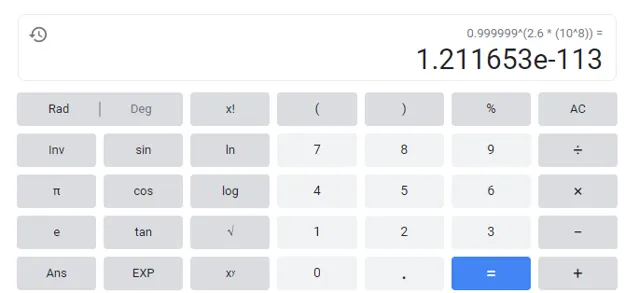
实际上,当仅经过了 2.6\times10^{8} 次反射后,也就是8.6秒后,能量就降低到只有最初的 10^{-113} 了。这是什么概念呢?全宇宙的总能量约为 4\times10^{70}\ \rm J [4] ,全转化为780 nm的光子( 2.55\times10^{-19} \ \rm J ),就是 1.57\times10^{89} 个光子。哪怕全宇宙的能量都照射过去,哪怕反射率已经达到了惊人的6个9,经过不到8秒后就甚至连一个光子都不剩了,更别提昨日重现了。
那么假设对于一般的99%的银镜,经过100次反射( 3\ \rm \mu s )后,能量就衰减至只有37%了;经过 30\ \rm \mu s 后就只剩下0.004%了。由此可见,企图使用镜子实现昨日重现,从能量的角度看,是完全不现实的了。这也是为何无法使用两个平行的镜子来储存光。
参考
- ^https://en.wikipedia.org/wiki/Hagen–Rubens_relation
- ^https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity
- ^https://en.wikipedia.org/wiki/Perfect_mirror
- ^https://zh.wikipedia.org/wiki/数量级_(能量)#大于1027











