特定情形下,三体问题是可解的,甚至某些特解非常简单。但是一般而言,三体问题不存在解析通解,即,我们无法用代数表达式写出任意构型下三体问题的通解。
二体问题的约化
要了解三体问题,首先可以从二体问题开始。
二体问题,顾名思义,研究的是两个物体在彼此相互作用下的运动,例如只考虑地球和月亮在彼此万有引力下的运动,就可以抽象为一个二体问题。将两个天体看作质点,设其质量分别为 m_1 和 m_2 ,初始位置分别为 \vec r_1 和 \vec r_2 ,初始速度分别为 \vec v_1 和 \vec v_2 ,根据牛顿运动定律,可以得到:
\vec F_{12}=m_1 r_1''
\vec F_{21}=m_2 r_2''
到此,我们写出了二体问题遵循的运动方程,剩下的问题便是解这组方程了。
使用高中物理中常用的质心的概念,可以将二体问题分解为质心的运动和两个天体相对于质心的运动。
质心的位置为: r_心=(m_1\vec r_1+m_2\vec r_2)/(m_1+m_2)
质心的运动是一个单体问题,而在质心坐标系下,两个天体对于质心的运动可以用两个天体之间的相对位移来描述,即
r_{相对}=\vec r_1-\vec r_2
r''_{相对}=(1/m_1+1/m_2)F_{12}
此处又变成了一个单体问题。所以,二体问题本质上可以理解为两个独立的单体问题的结合,分别求解这两个单体问题即可得到二体问题的解。
由于求解单体问题是比较容易的,因此二体问题作为可解问题,远远不如「表哥」三体问题名气大了。
三体问题溯源
时间回到1885年,学数学出身的瑞典国王奥斯卡二世赞助了一场有奖数学竞赛,竞赛的题目是4个数学难题,其中之一便是多体问题——求解太阳系的运动问题。
这一难题从牛顿时代提出直到竞赛发布之时,在学术界始终无人能攻克。众多数学物理大师先后折戟沉沙铩羽而归,甚至牛顿力学的奠基人牛顿本人,也只能写出其运动方程,然后在求解的过程中失去信心,认为这是「人类智力不可胜任的任务」。

面对被牛顿认为达到了人类不可解这种级别的难题,刚刚而立之年的庞加莱并没有退缩,他把问题进行了一些简化,只考虑三个星体,归纳为著名的「三体问题」。此后庞加莱奋笔疾书,在比赛提交的论文里发明了一种方法,可以求解任意精度的三体运动轨迹。
不久,赛事方接收了庞加莱的论文,审阅之后认可了他的解答,并给他发了比赛奖金,之后着手把这篇「旷世奇文」刊登在学术期刊上。就在这时,庞加莱发现,自己的解答错了。这下子事情就比较尴尬了。

庞加莱不得不支付了召回杂志等一系列补救措施的费用,虽然奖金并没有被收回,但是最后算下来,庞加莱还是亏了不少小钱钱的。

虽然参加比赛赢了奖金却亏了更多钱,但庞加莱还是在这个过程中收获了很多东西,比如,他提出了相图理论,并最终开创了混沌这一数学分支。庞加莱发现,一般性的三体问题往往是混沌的,即,如果两个三体系统的初始条件即使仅有一点点微小的不同,在后续的演化过程中,两个系统的动力学状态会产生巨大的不同。
混沌系统是确定的,例如三体系统的运动方程是可以用牛顿力学精确写出来的,三体问题在动力学上是确定的,没有随机性。但是混沌系统是不可预测的,因为初始条件的一点微小差别,会导致其之后运动状态的巨大不同,演化时间的增加会放大初值的微小扰动,导致我们无法判断其长期的轨迹。
这一切仿佛上帝开的一个天大的玩笑:我们可以写出它的方程,给定一个初始条件,我们甚至知道它的轨迹是确定的,但我们还是无法预测。
就像一座山,山就在那里,但触不可及,撩拨着探索者的心弦。
代数不可解与数值不稳定
三体问题的「不可解」体现在几个方面:
1、对于一般性的三体问题,无法写出一个解析通解。
我们没办法找到一个类似单体问题通解那样的数学表达式来描述三体问题。可能有小伙伴会问,是不是随着数学的发展,人们就能找到这样的代数表达式呢?
其实也是不可以的。在二体问题的分析中,我们已经知道,在三维空间有x,y,z 3个自由度,因此每一个天体可以写出3个二阶微分方程,如果改写成一阶微分方程,那就是6个。对于三体问题,就会得到18个一阶微分方程。求解三体问题,等价于解这个18个一阶微分方程构成的复杂的方程组。1941年,西格尔从数学上证明了,不可能找全这18个代数积分。所以,代数角度求积分来解三体问题的道路,已经被证明完全不通了。

2、对三体问题的数值解,会面临混沌的初值敏感问题。
既然直接代数积分找解析解行不通,那么为什么不用强大的超级计算机来求数值解呢?在很多领域,只要数值解精度足够,是可以胜任解析解的任务的。
虽然人们通过计算机来试图「开挂」,但是三体问题更狡猾,它是混沌的!
混沌系统的一大特点便是对初值敏感,如果给计算机的初始条件有一点小小的误差,例如我们想研究B612星球、赛博坦星球和奥特之星构成的三体问题,如果在输入程序的初始条件时,迪迦的战斗光线影响了天文望远镜对奥特之星速度的观测,导致了一个小小的误差,之后在经过一段时间的计算机模拟演化后,很可能算出一个和现实偏差巨大的结果,俗话说便是,「失之毫厘,谬以千里」。

于是一些小伙伴有疑惑了,如果我换用更精确的数值积分方法是不是就可以了呢?欧拉方法只取一阶不够精确,我换三阶龙格库塔法,甚至四阶龙格库塔法,不行再用更高级的积分方法......
很遗憾,并不是这样的。三体问题在数值上是「病态的」,即问题对初值敏感,就像「蝴蝶效应」一样,蝴蝶扇动翅膀的微扰都有可能造成一场龙卷风级别的计算偏差。病态问题是其数学上内禀的性质决定的,和计算方法无关,换积分算法并不能解决计算的不稳定性问题。
特解
一般的三体问题是没有解析通解的,但这不妨碍在某些特定构型下,三体问题有解析解,甚至是非常直观而简单的解析解。为什么呢?因为特解要求初始条件具有某些限制条件,例如保持一定的对称性,或者初速度具有某种规律。这些条件其实是对一般性三体问题的约束,增加约束可以减少问题的自由度,当自由度足够少,便可以解析求解了。
第一种存在特解的情况便是,把三星摆在一条直线上,然后让两边的星体围绕中间的星体做圆周运动。
其次可以把三星摆在等边三角形的三个顶点上,让它们围绕三角形中心做圆周运动。
稍复杂一点的构型是将它们摆在8字型轨道上,也可以使用解析表达式对其运动进行描述,如下图:
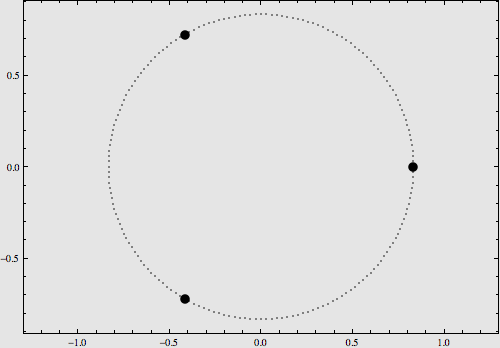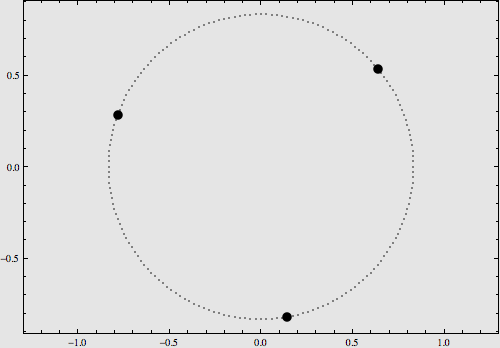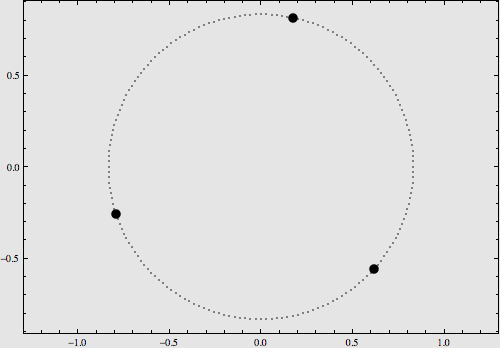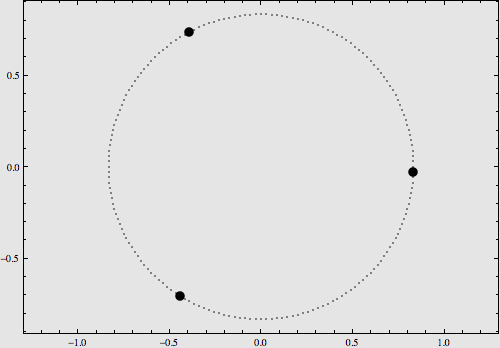
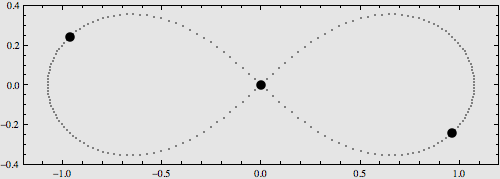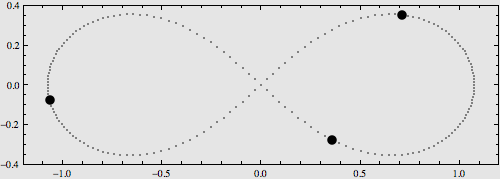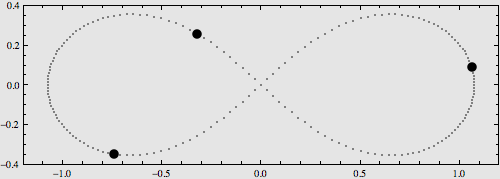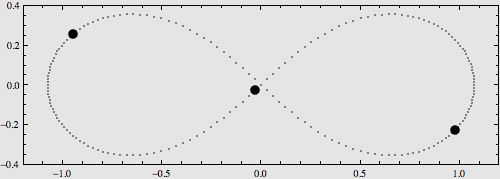
更多的特解不再一一列举。
三体问题是混沌的,对于其短期内的动力学轨迹,我们可以使用数值方法进行模拟,甚至可以达到非常高的精度。但是对于其长期的动力学轨迹,解析解已经不奢望了,数值解也只能参考参考,就像第二天的天气预报往往很准确,但是15天后的天气预报往往只能参考参考。也许,屏幕前的你打了个哈欠,就能影响地球某个地方未来的天气呢~











