恶老师秘制数学小汉堡,富含维生素abcdefg,大体难度不超过★★★☆☆,非常适合智力中等及以上人类食用。

强行掺入微量 初等数论 ,用以提鲜,剂量极小绝不致死……


仪式完毕,正文马上开始!^_^
弱弱斗胆说一句:本答案应该是目前所有回答里最全最细致最明白的,写作中途我也遇到了困难整整想了3天才解决。
说实话这个问题看似极其简单,深挖起来简直深不见底。
本文从计算1/49循环节这样小学生都会的难度,一直层层递进,带你穿过欧拉定理,直至触碰到世界未解数论难题,这其中的冒险实在是非常刺激,一路上我已经为大家披荆斩棘,难度压到最低,欢迎来我的数学胎教乐园玩耍!^_^(强行诱捕上车)
全文手码为爱发电!!望点赞!!有任何bug欢迎指出,因为我写字真的特别粗心,复制黏贴都会弄错的那种,感谢!!!
(文末有彩蛋福利,请大家坚持看完!)
!!重要更新!!
关于正整数倒数循环节长度问题,我已经有了更为一般性的解答!!欢迎取阅!!
趣味详解版:
无情精简版:
如果你的数学基础比较差,建议先阅读本文哦~~~
〇、你的计算器不对劲,你更不对劲(难度:★☆☆☆☆)
首先我真的要吐槽题主,你那个计算器屏幕太小了,连1/49的循环节都显示不完整,你看看我的大屏计算器效果多好:
而且题主的描述也很不对劲:

所以你以为回答就到这里结束了吗?
天真!!!
恶老师的数学胎教~才刚刚开始!!!宝贝们快快上车!
一、1/49,没在怕的!(难度:☆☆☆☆☆)
有一件事情是肯定的:能写成分数的必是循环小数(不循环小数可以看作循环节为0),并且循环节出现是因为余数有限(余数的数量必然小于除数)。
所以看到1/49,真没在怕的,它余数的数量不可能超过49,循环节位数也不可能超过49。
尽管你的计算器不行,但是你的手行啊!
笔算一下1/49的小数部分,很容……很难吗?!
二、嘻嘻,1/49其实是一个2位有限小数(难度:★☆☆☆☆)
这个很有意思,并且我看了下,好几个回答已经提到了,但奇怪的是,点赞不多,估计是很多人脑子没转过来。
所以我再讲解下,在7进制的胎位下,你怀的崽子只有7根手指,他的世界里就是逢七进一,十进制的6还是6,十进制的7却成了10,49正好是7的平方,所以十进制的49就是七进制的100,化成分数1/100=0.01。
明白了吧?
不过正经人谁用7进制啊,你考试敢用7进制答题吗?
不敢吧!
所以我们还是得老老实实地回答这个问题:
为什么在10进制下,1/49写成小数,循环节那么长呢?有什么办法能够分分钟算出循环节长度吗?
这,才是一个好问题。
三、配一把万能钥匙(难度:★☆☆☆☆)
对我来说,如果要确定循环节的长度,就必须先搞明白,任何一个循环小数写成分数应该是什么样子——这就是我要配的钥匙了。
为了方便,这边只考虑 纯循环小数 ,就是从小数点后第一位就开始循环。
显然,在10进制下,纯循环小数分母的因数不能包含2或5,举几个例子:
1/7的分母既不包含2也不包含5,所以它是纯循环小数0.142857 142857 142857...;
1/27的分母也是既不包含2也不包含5,所以它也是纯循环小数0.0370 0370 0370...;
1/15的分母包含5,所以它是混循环小数0.066666...,它可以看作纯循环小数2/3=0.666666...的十分之一;
1/6的分母包含2,所以它也是混循环小数0.166666...,它可以看作是上面的1/15再加上0.1。
因为在本问题中,主要目标是确定循环节位数,所以就把混循环小数踢到一边,只需管好纯循环小数就够了。
现在,我们设这个纯循环小数的 循环部分 为 k_{1}k_{2}k_{3}...k_{m} 。
循环小数,感觉没完没了,怎么样和干净利索的分数产生关系呢?
当然是得想办法 消掉循环小数的循环部分 呀!
这个办法就是错位相减法。
比如5/11的循环部分是45,就给5/11乘上100让它小数点移2位,然后和5/11相减,循环部分就没啦!效果立竿见影:
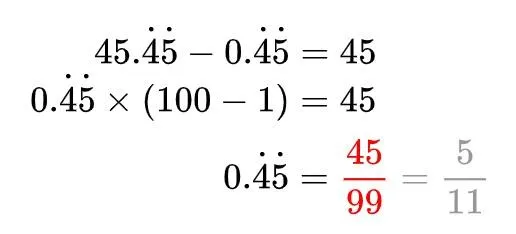
观察一下上式规律,我们就可以打造出「纯循环小数化分数」的万能钥匙了:
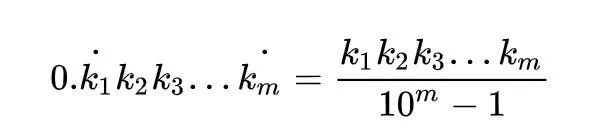
好了,现在就用这把钥匙,把1/49变成循环小数的形式:
1/49的分母49的因数,既没有2,也没有5,判断1/49一定是纯循环小数,所以可以套用这把万能钥匙,把1/49写成这样的分数形式:\frac{1}{49}=\frac{k_{1}k_{2}k_{3}...k_{m}}{10^{m}-1}
四、欧拉~o了?!(难度:★★☆☆☆)
刚刚我们已经得到了: \frac{1}{49}=\frac{k_{1}k_{2}k_{3}...k_{m}}{10^{m}-1} 。
为了让式子更简洁,我们来把这个式子变个样:
10^{m}=49\times{k_{1}k_{2}k_{3}...k_{m}}+1
这时候,就可以发现,这个式子是在说: 10^m除以49余数为1 ,即: 10^{m} mod49=1
我当时就胎动了一下,感受到了欧拉定理的召唤,赶紧把式子写成:
10^{m}\equiv1(mod 49) ,即10^m与1对模49同余
很快啊!我赶紧和欧拉定理对接,欧拉定理长这样:
a^{\varphi(n)}\equiv1(modn) ,即 a^{\varphi(n)}\ 与1对模n同余
你看看!前面那式子是不是和欧拉定理亲生的一样!
眼看就顺产成功了,还愣着干啥呀,赶紧把n=49代到欧拉函数\varphi(n)=n(1-\frac{1}{p_{1}})(1-\frac{1}{p_{2}})(1-\frac{1}{p_{3}})...(1-\frac{1}{p_{k}}) 里!
\varphi(49)=49(1-\frac{1}{7})=42
我当时一看到42就以为哦了完事了,毕竟前面我的大屏计算器算出了m也的确是42没错。
然后我想当然地以为m= \varphi(n) ,准备文章收尾的时候,突然感到不对劲:
如果循环节长度 m=\varphi(n) ,根据欧拉函数特性当n为素数时 \varphi(n)=n-1 ,但尼玛1/3的循环小数位显然是1不是2啊!!!!!
我这时候慌了,赶紧翻了下这个问题下的其它回答,看到有几个提到结论是m是 \varphi(n) 的约数,再一算,n为素数43的时候, \varphi(n)=43-1=42=\varphi(49) ,也就是说1/49和1/43的欧拉函数都是42,但1/43的循环节长度不是42,而是21!我当时就愣了,哪里错了?
嗯……我老实交代,上面那个问题居然让我想了2天,因为我误以为是前面万能钥匙那一步m设得有问题,验算了n遍,我以为我是傻,后来我才突然发现,我是瞎……
我竟然看着 10^{m}\equiv1(mod 49) 和 a^{\varphi(n)}\equiv1(modn) 想当然地以为 a^{42}=10^{m} ,但事实是 a^{42}\equiv10^{m}\equiv1 (mod49)
这两个式子意思天差地别!前者 a^{42}=10^{m} 意味着m只有唯一解42,后者 a^{42}\equiv10^{m}\equiv1 (mod49) 意味着m的解不止一个,即m可能为42约数中的任何一个,m为1、2、3、6、7、14、21、42的其中一个!
所以光用欧拉定理还是不能完全确定m的值啊!!
偏偏这个42的约数还特别多,烦死了!!!(TAT),怎么办啊!!!枚举法我是拒绝的!!!更可恶的是这个问题看起来貌似极其简单……
五、冒险越来越深入了……(难度:★★★☆☆)
高能预警:这段的难度主要在于术语理解,逻辑是很简单,难度相当于中国人看美国八卦报纸,你英语好看起来很容易,都是家长里短的破事,你英语菜看起来不知所云以为是什么高大上的东西。
温馨提示:这段对没有数学基础会有难度,可以直接跳到六,六是真刺激。
最终我又花了1天时间现啃了一堆资料,就硬啃,最终终于明白事情如此简单:
我要求的m,被称为「10模49的阶」。
抽象吧?不准下车,车门已经焊死了,你就陪陪我走到底吧!我这3天简直就像在黑暗里独自前行,永远不知道下一个坑在哪里!
嗯,回到刚刚那句话,「10模49的阶」,你就当阅读理解做,这其实不是一个数学题,而是一个语义疯狂套娃的脑筋急转弯!
「模「没什么好说的,就是取余数,至于这个」阶「是什么,真得好好解释下:
对于欧拉定理 a^{\varphi(n)}\equiv1(modn) ,当a和n互素(这句条件等价于1/n为纯循环小数),此时满足 a^{x}\equiv1(modn) 的x存在最小正整数解,这个x称作a模n的阶,并且这个阶要么等于 \varphi(n) ,要么是 \varphi(n) 的约数。
别慌,这句话的关键词就两个字「约数」。这足以一半解答了我们的疑惑。前面我们发现,1/49和1/43的欧拉函数同为42,但1/43的循环节长度为21,本质是因为循环节长度并不等于欧拉函数的值,而是这个值的约数,也就是说,目前的全部推理,只能确定它俩的循环节长度为1、2、3、6、7、14、21、42的其中一个,只不过1/49的循环节长度正好落在了最大值。
那么问题来了,这「阶」怎么求呢?哎,这时候又必须要谈「原根」:
若a模m的阶等于φ(m),则称a为模m的一个原根。
这句话对于大多数人来说应该还是天书,但其实数学证明很多时候就是颠来倒去说同一件事。
可以肯定的是,10是模49的一个原根,且它的阶正好就是 \varphi(49)=42 ,所以1/49的循环节长度是42。
那么问题来了,有什么 \varphi(n)=42 ,阶却不是42的n呢?
因为 10 不是 43 的原根,所以 10模43的阶不是42,是21。
至于原因,我已经在开头给出的链接中非常详细解答了,欢迎大家阅读!!
六、后记
因为我是业余学习的数学,数论也是因为觉得这个 1/49 的问题有趣,临时学的
所以一开始我几乎没有任何知识储备,甚至天真地以为对于任意正整数 x ,人类应该已经有一个确定的什么函数 f(x) 可以无需枚举就能得出 1/x 的循环节长度,但到处都搜不到答案,
于是我就开始「闭门造车」,研究了很久,一直发现没有结果,这个过程非常煎熬
最终通过自己持续不断的思考,终于发现这个问题最终指向了一个终极难题:大数分解,本质上触及了黎曼猜想(关于这一点,我在开头给出的链接也详细解答了)
——嘻嘻,那我解不出也是理所应当的嘛!
这样的经历给我带来非常神奇的体验,以下是当时的心情记录:
……我就想办法自己找这个函数,因为我感觉这个问题看起来极其简单,诡异的是我研究了一整天都没找到办法……我仔细翻看了这个问题下的所有答案,竟然没有人能解答我的问题。
难道……是我的问题太简单了吗?
我呆呆地写了十页纸,反反复复验算,希望不断被点亮、熄灭、点亮、熄灭,我逐渐感叹自己是不是智商不配碰数学,这么简单的问题,算不出来一定是因为我太笨了……
我很明显感觉到自己在一个怪圈里打转死都出不去。这种感觉非常恐怖,就好像在一片漆黑的森林里寻找回家的路,走了很久发现自己还在原地,感觉永远没有出头之日,然而心底却又有一个声音不停和我说,你再撑一下就到家了!
最终,我还是放弃了,我承认自己不行,于是拿手机刷了很久乱七八糟的东西放松,然而我满脑子都是那个问题,根本挥之不去,于是我打开电脑不停换关键词搜,我先是在一篇小论文看到了一个叫做Artin猜想的东西,我突然意识到了什么,让我喜出望外,但那也不是我要的的东西,我继续不停检索,终于突然搜到了「最小正原根上界问题」,我感觉希望之光又被点燃,赶紧看下去:
华罗庚于1942年应用狄利克雷特征函数的概念及三角和的估值方法,在估计最小正原根的上界方面,得到了很好的结果,他证明了:g(p)<2^r*p^(1/2),其中r是φ(p)=p-1的不同质因数的个数。
1959年,王元证明了g(p)=O(p^(1/4+ε))。
(可能我没有找到最前沿的资料,但这个问题似乎真没有完美解决,求大佬给我一个痛快)
我瞬间站了起来,我和我老婆说我竟然自己发现了世界级的数论难题!
我老婆正在忙她的画,似乎一下子没明白我在说什么。
我就和她说:「可能你不知道我在说什么,但我依旧想和你传达我的喜悦。」
我老婆就像往常一样夸我:「老婆太强了!」
尽管我此时可以为我的小聪明欢呼,但事情却细思恐极……
我,追随着一只1/49的美丽蝴蝶,等我扑到它,又出现一只蝴蝶1/43,这时我发现刚刚抓到的1/49蝴蝶又逃跑了,我就一路追过去,越来越累,却还是不停跑,等我反应过来才发现,四周早已漆黑一片,我努力寻找人的踪迹,找了好久好久,才看到有人立了一块牌子:「恭喜你到达边界,我们都没有走出去,你想再挑战一次吗?」
我的直觉告诉我赶快跑,不要在这个地狱一样的边界逗留!我一边跑,周围的风景一边回溯,一群素数的蝴蝶开始飞舞,一会儿组成最小原根上界猜想,一会儿组成Artin猜想……一会儿又是大数分解难题,一会儿又是黎曼猜想……
这玩意不是胎教,这玩意有毒啊啊啊!!!!
小恶、收刀入鞘、全身而退吧!!
突然间,我放下执着,一切都恢复了往日的平静。最近缺乏睡眠的我,只感觉浑浑噩噩,一想起这三天的经历,宛如做了一个荒唐的梦。
……恐怖如斯,不可名状!起点如此简单,只不过是自然数而已,并且我的每一跨步都不大,却只消五步就踏到了学术的边界……这种空间的失控感,简直诡异至极!
ho!原来数论就是数学的五步蛇!!!23333
~~ ★压压惊:传统美德之 文末福利 ★ ~~
以下是我写这篇文章的内心戏:



总之,这次神奇的经历,让我与数学结下不解之缘
我决定投入更多的时间学习数学
目前在蜗牛般自学数学分析和抽象代数,我对这两个分支非常感兴趣
在学习过程中的任何见解,我都会无条件地分享给大家,共同进步~~










