声子频率与温度有关
但是这种关系很复杂,不能直接的描述为温度的函数形式。
之前借用分子动力学软件计算了某种金属的声子态密度的一个小练习(势函数采用的是经验势)。方法是从MD模拟中得到速度自关联函数,然后傅里叶变换就得到声子DOS。
这里面我没有去算某个模的频率,我也算不了。但是可以从态密度里面看出一些东西。
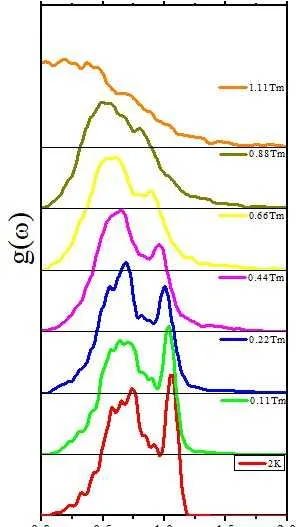
我们可以看到:(1)随着温度的升高,更多的声子模向低频偏移,这就是通常的大多数材料在高温下的声子软化,在温度升高的情况下,原子间距一般会增大,导致力常数较小,使得频率减小,(这是与热膨胀相对应的,当然有的材料在升温下会热缩);(2)随着温度升高,在高频,声子态密度有更长的拖尾效应,这是由于高温下的声子声子相互作用(PPI)造成的,多个低频声子耦合为一个高频声子。
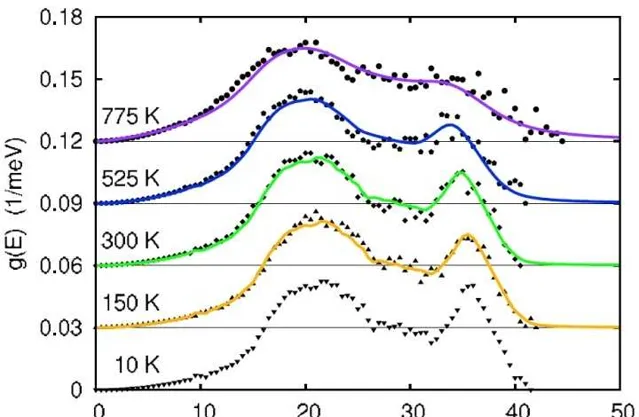
这个结果和上面计算的结果大体趋势是差不多的。
二次量子化形式下的声子频率
系统的哈密顿量可以写为
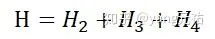

其中p,p,p分别为哈密顿量的二阶项、三阶项和四阶项, \Phi 为力常数。三阶项和四阶项可进一步写为(引入产生湮灭算符):
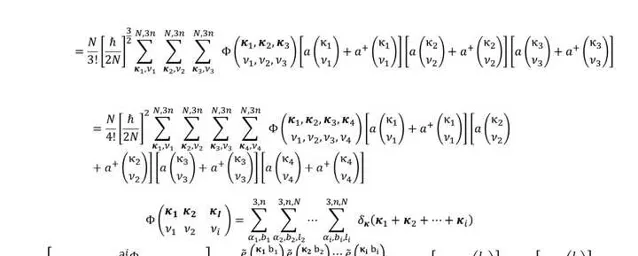
忽略中间的一些细节,得到声子频移

以上是一种计算非谐效应的方法。
里面虽然没有关联到温度,但实际上哈密顿量的三阶项p和四阶项p是和温度有关的。 \Phi_{\alpha_1,\alpha_2,\alpha_3} 和\Phi_{\alpha_1,\alpha_2,\alpha_3,\alpha_4} 就是三声子过程和四声子过程。
一、简谐近似下的声子频率
在教科书中,单原子链格波色散关系表示为:
\omega=2\sqrt{ \frac{\beta}{m} }|sin\frac{1}{2}aq|
连续介质弹性波 \omega=v_{s}q
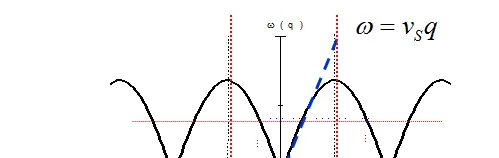
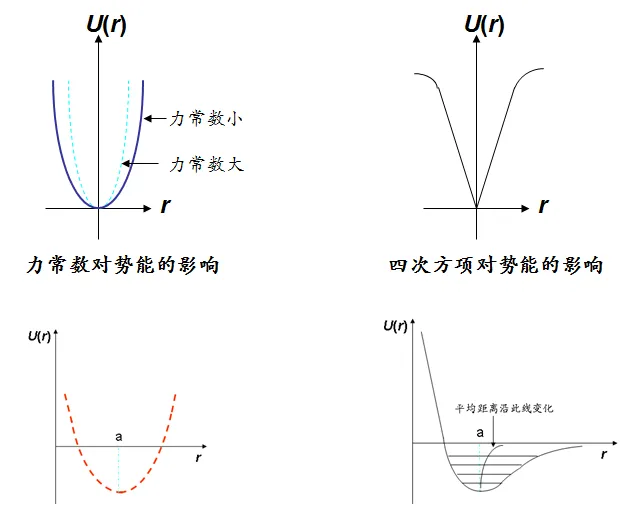
我们看到,声子频率只与 力常数\beta
有关。在简谐近似处理下
2、相互作用势能的非简谐项

非简谐项,代表原子之间排斥作用的非对称性
非简谐项\frac{1}{6}g_{0}\delta^3 ,代表原子之间排斥作用的非对称性,
δ>0时,\frac{1}{6}g_{0}\delta^3 小于0,势能减小
δ<0时,\frac{1}{6}g_{0}\delta^3 大于0,势能增大
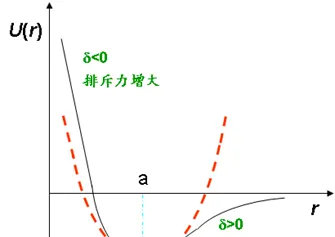
•考虑这一非简谐项后,势能曲线不对称:δ>0一边比较平缓,δ<0一边则比较陡峭。因此非简谐振动,使原子间产生一定的相互斥力,从而引起热膨胀。所以热膨胀是一种晶格振动的非简谐效应。
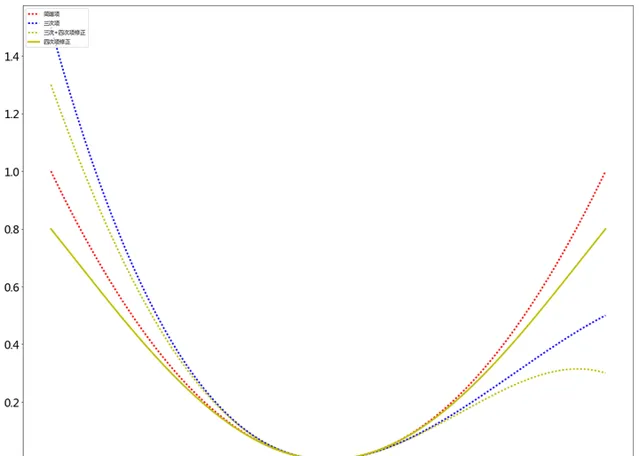
非简谐项\frac{1}{24}h_{0}\delta^4 , 代表在大振幅下振动的软化
考虑二阶项和四阶项,有
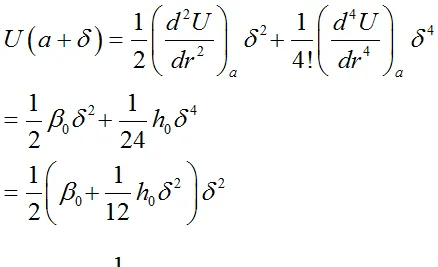
回复力常数减小,振动软化。
U(a+\delta)=\frac{1}{2}\beta_{0}\delta^2+\frac{1}{6}g_{0}\delta^3+\frac{1}{24}h_{0}\delta^4
3.非简谐近似下的解
(这个并不容易,因为现在的微分方程已经不是简单的二阶常微分方程)
考虑谐振子方程中的非简谐项,双原子运动方程
\mu \ddot{ \delta} =f(\delta) =-\frac{\partial U}{\partial \delta}=-\beta _0\delta-\frac{1}{2}g_0\delta^2 \\
μ是两原子的约化质量
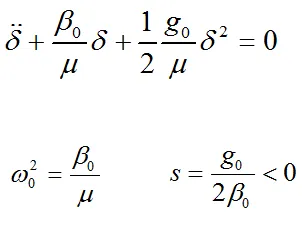
运动方程解的形式\delta=v_{0}+A(cos(\omega t)+\eta cos(2\omega t))
这里只考虑了Fourier展开式中的头三项,所以只有2w项,如果考虑d3项,则会有3w的项。p将方程的解代入运动方程,并假定sA<<1,有
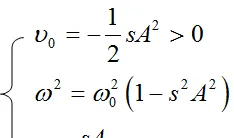
利用方程的解,并考虑<coswt>=0, <cos2wt>=0

因为g0<0,所以a(T)>a
当系统与热源处于热平衡状态时,双原子的平均振动能
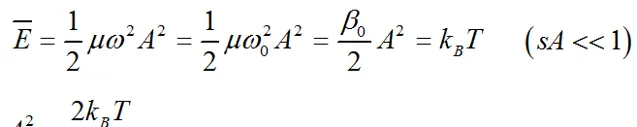
振幅的平方与温度成正比
可以得到
a(T)=a_{0}-\frac{1}{2}\frac{g_{0}}{\beta_{0}^2}k_{B}T
\color {red} {\omega^2(T)=\omega_{0}^2(1-\frac{1}{2}\frac{g_{0}^2}{\beta_{0}^2}k_{B}T)}
随着温度的升高,原子间距离增大,作用力下降,振动频率减小。上式就给出了频率与温度的关系,看起来简单,但还需要求解 g , \beta ,此外,这个式子依然没有考虑声子耦合(PPI)。











