本篇文章是深入浅出GPU优化系列的第两个专题,主要是 介绍如何对GPU中的矩阵乘法(GEMM)进行优化 。目前针对GEMM的优化,网络上已经有非常多的教程和示例了。大部分的重要资料我都看了看。但总的来说,还是不够接地气,然后理解起来还是会比较费解。所以希望写这么一篇文章,尽可能地去把GPU的GEMM优化说清楚,说明白。然后让小白读者也能通过这么一两篇文章去更好地了解GEMM优化的相关技术。
不像上次的reduce优化一样,能一篇文章说完。这次的GEMM优化会分为三个部分。 第一个部分只说优化思路和分析 ,没有任何代码,这么做考虑也是为了减轻读者的负担,看代码太累, 尽可能地让读者先明白原理,为什么要这么做 。 第二个部分是对代码的详细解析,这个里面就是一行一行地去分析代码 。因为之前的很多博客进行了分析,但是代码本身并没有开源,或者说开源了代码,但没有解析,看起来太累了。我希望提供一个尽可能详细的代码解析,读者看完之后能明白相关优化技巧,并且可以直接把代码拿去验证使用。 第三个部分主要涉及到汇编器 ,最重要的是说明在NV的卡上,怎么去解决寄存器的bank冲突来获取极致的性能。
本篇文章是 GEMM优化的第一个部分 ,在这篇文章中,只说 优化思路和分析 。
前言
在高性能领域,对于 矩阵乘(GEMM)的优化 是一个非常重要的课题。GEMM可以非常广泛地应用于航空航天、流体力学等科学计算领域,这也是之前HPC的主要应用场景。后来深度学习开展地如火如荼,由于对高算力的需要,也成为HPC的主要应用场景之一。这些年涌现了一系列的深度学习模型。模型里面最耗时的东西,包括卷积、全连接层、attention,都可以转换成GEMM操作。所以说,GEMM优化的重要性,怎么突出都不过分。
目前网上能找到的针对GEMM优化的资料主要有这么几个方面:
一、论文
,目前针对GPU进行GEMM优化的论文非常多,这里主要推荐Understanding the GPU Microarchitecture和Fast implementation of dgemm on fermi gpu以及 Dissecting the NVIDIA Volta GPU Architecture via Microbenchmarking。这几篇论文在业界都比较有影响力,就是代码开源方面做的不算太好。
二、官方博客
,主要是CUTLASS和NervanaSystems-SGEMM优化。还有前段时间旷视发的文章CUDA矩阵乘法优化,写的都很详细。
三、github
的一些demo,代码量不大,看起来比较舒服。我是看了这两个,
demo1代码写的好理解一些,但是优化工作没做完全,没有做到prefetch。demo2是效果很好,11个优化技巧,不断逼近cublas。但是代码真的看起来比较难受,最重要的很多参数写死了,不好去调。
总而言之,目前列举的上述资料存在着这么两个问题:一、文档方面,读起来还是比较费劲,对于小白来说,还是不够简单不够傻,看起来太累了;二、代码方面,要么是没公开代码,要么是代码太多了,看不下去;还有的就是代码可读性很强,但是优化工作还不是特别深,或者就是代码优化做的很好,但是可读性差了。方方面面总是有点欠缺,所以希望能够写一篇尽可能地在文档上简单明了,在代码上详细且可读性好的文章。当然,这是一个逐步迭代的过程,所以这篇文章也会持续进行更新哈。
本篇文章主要是采纳了cutlass的行文思路,主要介绍GEMM中的数据分块和如何在多级存储进行数据搬运。这也是 HPC优化的核心思想,怎么样让数据放在更近的存储上来掩盖计算的延时,从而减少存储墙的影响 。文章分为四个方面进行叙述,首先介绍在global memory层面如何进行分块以及数据搬运,随后介绍在shared memory层面如何进行分块以及数据搬运,而后介绍在register层面如何进行分块以及避免bank冲突,最后介绍如何进行prefetch以更好地掩盖访存时延。
从global memory到shared memory
假设有矩阵A,B,需要计算矩阵A和B的乘,即矩阵C。A、B、C三个矩阵的维度分别为m*k,k*n,m*n\ ,且三个矩阵中的数据都是单精度浮点数。对于C中每一个元素,C[i][j],可以看作是A的一行和B的一列进行一次归约操作。采用最naive的GEMM算法,在GPU中,一共开启m*n\ 个线程,每个线程需要读取矩阵A的一行与矩阵B的一列,而后将计算结果写回至矩阵C中。因而,完成计算一共需要从global memory中进行 2mnk\ 次读操作和m*n次写操作。大量的访存操作使得GEMM效率难以提高,因而考虑global memory中进行分块,并将矩阵块放置到shared memory中。其示意图如下:
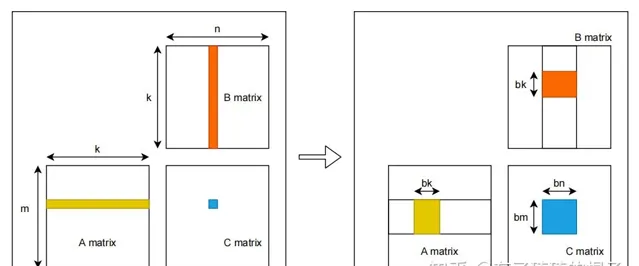
对global memory进行分块的GEMM算法示意图见上图右侧。首先将A、B、C三个矩阵划分为多个维度为bm*bk,bk*bn,bm*bn\ 的小矩阵块。三个矩阵形成M*K,K*N,M*N\ 的小矩阵网格。其中,M=m/bm,N=n/bn,K=k/bk\ 。随后在GPU中开启M*N\ 个block,每个block负责C中一个维度为bm*bn\ 的小矩阵块的计算。计算中一共有K次迭代,每一次迭代都需要读取A中一个维度为bm*bk\ 的小矩阵块和B中一个维度为bk*bn\ 的小矩阵块,并将其放置在shared memory中。因而,完成C中所有元素的计算一共需要从global memory中读取M*N*K*(bm*bk+bk*bn)\ ,即m*n*k(1/bm+1/bn)\ 个单精度浮点数。相比于naive的GEMM算法,访存量减少为原来的 1/2*(1/bm+1/bn)\ 。通过global memory中分块算法极大地减少了对global memory的访存量。并且,相比于naive算法,对global进行分块可以更充分地利用数据局部性。在naive算法中,每一个线程都需要直接从global memory中取数,其时延非常长,计算性能非常差。而进行分块后,将维度为bm*bk,bk*bn\ 的小矩阵块先存储到shared memory之中。而后计算单元进行计算时可以直接从shared memory中取数,大大减少了访存所需要的时延。
从shared memory到register
随后,我们进一步考虑从shared memory到register的过程。在这里,只分析 一个block 中的计算。当进行K轮迭代中某一轮迭代时,GPU将维度为bm*bk,bk*bn\ 的小矩阵块存储到shared memory中,而后各个线程将shared memory中的数据存入register中进行计算。

在 不对shared memory分块 时,一个block中含有bm*bn\ 个线程, 每一个线程负责C中一个元素的计算 。则一个block一共需要对shared memory进行 2*bm*bn*bk\ 次读操作。而后 考虑对shared memory进行分块 ,对bm*bn\ 的小矩阵进行再一次划分,将其划分为多个维度为rm*rn\ 的子矩阵。则一个block需要负责X*Y\ 个子矩阵。其中,X=\frac{bm}{rm}\ ,Y=\frac{bn}{rn}\ 。随后,在一个block中开启X*Y\ 个线程, 每个线程负责一个维度为rm*rn\ 的子矩阵的计算 。在计算中,一个block一共需要从shared memory读取X*Y*(rm+rn)*bk\ ,即bm*bn*bk*(\frac{1}{rm}+\frac{1}{rn})\ 个单精度浮点数。相比于未分块的算法,对于shared memory中的访存量减少为原来的 1/2*(\frac{1}{rm}+\frac{1}{rn})\ 。并且,由于将数据放入register中,可以直接对数据进行运算,减少了从shared memory中取数的时延。
register分块
在这里,我们考虑最后一层,即register中的计算,并且只分析一个thread。在完成以上的过程后,对于一个线程而言,它现在拥有:rm\ 个A矩阵的寄存器值,rn\ 个B矩阵的寄存器值,以及rm *rn\ 个C矩阵的寄存器值。通过这些寄存器的值,需要计算rm*rn\ 个数。这需要rm *rn\ 条FFMA指令。
这个时候会涉及到寄存器的bank conflict。在NV的GPU中,每个SM不仅会产生shared memroy之间的bank 冲突,也会产生寄存器之间的bank冲突。这一点对于计算密集型的算子十分重要。像shared memory一样,寄存器的Register File也会被分为几个bank,如果一条指令的的源寄存器有2个以上来自同一bank,就会产生冲突。指令会重发射,浪费一个cycle。PS:这个地方是从旷视的博客中看的。然后对于maxwell架构的GPU而言,bank数为4,寄存器 id%4 即所属bank。
我们假设对这个thread来说,rm=4,rn=4\ 。并且计算C的寄存器以一种非常naive的情况分配,如下图左侧所示。则需要产生16条FFMA指令,列举如下:
FFMA R0, R16, R20, R0
FFMA R1, R16, R21, R1
……

可以从中看出,这会产生大量的register bank冲突,所以需要对参与计算的寄存器重新进行分配和排布,如上图右侧所示。在有些地方,这种方式也可以叫做register分块。
数据的prefetch
最后,我们来讲讲如何通过对数据进行prefetch来减少访存的latency。我们再来回顾GEMM的过程,并且仔细地看看这个访存的latency到底是怎么导致的。 对于一个block而言 ,需要计算一个bm*bn\ 的矩阵块,这个时候需要进行K次迭代,每次迭代都需要先将来自A和B的两个小块送到shared memory中再进行计算。而从global中访存实际上是非常慢的,所以导致了latency。虽然GPU中可以通过block的切换来掩盖这种latency,但是由于分配的shared memory比较多,活跃的block并不太多,这种延时很难被掩盖。 对于一个thread ,需要计算一个rm*rn\ 的小矩阵,但是必须先将数据从shared memory传到寄存器上,才能开始进行计算。所以导致了每进行一次迭代,计算单元就需要停下来等待,计算单元不能被喂饱。
为此,需要进行数据的Prefetch来尽可能地掩盖这种latency。思想也比较简单,需要多开一个buffer,进行读写分离。示意图如下。当block进行第2轮迭代时,需要对A2和B2进行计算,在计算单元进行计算的同时,我们将A3和B3提前放置到shared memory。而后,在进行第3轮迭代时,就可以直接对shared memory中的A3和B3进行计算,而不需要等待从global memory搬运到shared memory的时间。寄存器上的Prefetch也是同理。

总结
GEMM的优化思想,基本上就是这么几方面的内容。希望大家通过介绍能够对GEMM的优化有一个比较直观且具体的理解。(感觉写的还是有点乱,图也没画的太好,大家谅解)。当然,看完这些,要开始写代码的时候,大家还是会比较懵,也不知道这些东西应该怎么实现。现在写了详细的解析,也就是GEMM优化(二)。去实现了上述优化技巧和细致地分析每一行代码,大家可以看一看。
第三部分中,更细粒度的CUDA C代码调优和关于汇编代码的调优,也已经给出。
最后, 感谢大家看到这里,有什么问题欢迎跟我讨论哈 。关于GPU的优化,打算写一个系列,说说GPU优化的一些经典问题和优化技巧。不过最近工作也比较忙,更新估计很慢。之前已经写完了
的内容。希望后面能坚持下去。
欢迎大家关注哈:)











