严谨一点的回答是,汉语是世界上信息熵最大的主流语言。
1948年,香农的【A mathematical theory of communication】一文震撼了学术界,从此开创了一个信息度量时代。既然事件发生的信息可以度量,语言也是一种信息传递手段,那么语言中的信息究竟是多少?世界上有最优的语言吗?
在正式开始之前,我们先来谈谈信息熵跟信息量之间的关系。
信息量是事件可能性不确定度的度量, 第 i 个可能性中信息量是 -logP_i , 比如明天下雨有下雨不下雨两个可能性,下雨的概率是 P_1 ,那么下雨的信息量就是 -logP_1 .
信息熵指的是事件发生的所有可能性中包含信息的期望平均值,
H(X)=-\sum_{i}{P_i}log {P_i} 。
这里的「事件」可以指代任何随机发生的事情,比如提笔写下随机一个字。如果对上述定义不是很理解的话,可以参考下边这个回答~
那么,如果想要计算一个事件的信息熵,需要什么要素呢?从信息熵公式,很明显可以看出是 事件发生的所有可能性,以及对应的概率。
我们为什么要计算语言的信息熵呢?
抛开兴趣不谈,其实从科学研究角度,语言的信息熵研究也有着非常现实的意义。如果可以准确的计算出语言的信息熵,那么就得到该语言的信息压缩的下界,即文本压缩算法到达这个界限再也无法压缩。这种算法就是该语言的最优压缩算法,不需要继续优化辣。
现在可以回到原来的问题, 语言的信息熵究竟是多少?
这个问题的计算方式其实很直观,只需要代入信息熵的公式就可以了。但是困扰信息论和语言学者将近一个世纪的问题是, 我们无法准确地知道一个语言中特定文字的出现概率,甚至有时难以统计某种语言中究竟有多少种字符 。
信息论科学家只能通过各种手段来 估计 各个语言的信息熵,比如Shannon认为英语的信息熵在0.6到1.3bits/字之间[1],Cover和King则认为英语的信息熵是1.25bits/字[2]。差异来自于样本和实验方法的不同。英语等表音文字只有24个字母, 但是对于汉语,统计难度就大大增加了。幸运的是,当年信息论发展不久,各行各业的科学家都投入了极大兴趣来探索各种语言,即使中文有很大的特殊性,信息论前辈们也排除万难,用统计采样的方式计算了汉语的信息熵[3](数据集不完备),
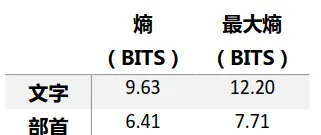
很明显,中文不论从以文字,部首还是音节作为统计基础,其信息熵都远远超过英语。
看到这里各位观众可能觉得已经满足了, 但是这样计算出的实验结果并不能与其它语言直接对比 。因为上述实验基于不同的数据集,不能确定实验样本是否蕴含着等量的信息,同样不能排除翻译人员的个人原因导致的信息误差。
2002年,哈佛大学的Frederi等人重新做了对比实验。他们认为,从过往的自然语言研究来看,自然语言都有着很多共同的统计特性和相似的模式。他们假设,对不同种类的语言,类似PPM这种基于马尔科夫的压缩算法会忽视语言特性,把文本压缩至逼近信息压缩下界[4]。
换句话说,如果采用的压缩算法不是针对某种语言特殊优化,不同的语言可以通过比较算法的压缩效率来近似比较信息熵。因此他们设计了一个实验,采用PPM算法压缩了各种不同版本的圣经:
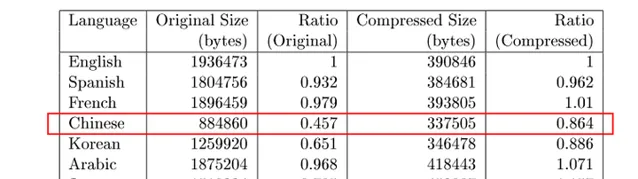
如上图中,研究者们对比了英语,西班牙语,法语,中文,汉语,阿拉伯语,日文,俄语这些不同版本圣经的压缩前文件大小,压缩前文件大小与英文文件的比例,压缩后文件大小,压缩后文件大小与英文文件的比例等属性。理想条件下,如果翻译,压缩等过程没有信息损失,压缩后其他语言文件大小与英文文件的比例应该等于1。
我们可以很明显看到,中文的压缩效率低于其他文字,但是这个压缩效率是不是由于文本和压缩算法的原因引起的呢?他们又完成了如下两个实验,
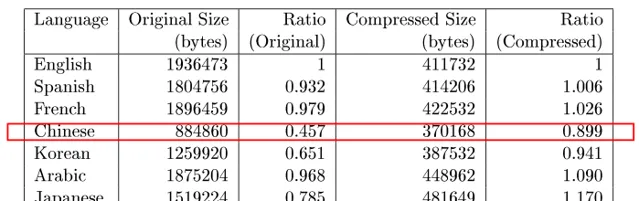
第二个实验中采取了不同的压缩算法(BZIP2),结果相似,说明并不是压缩算法导致的压缩效率低下。
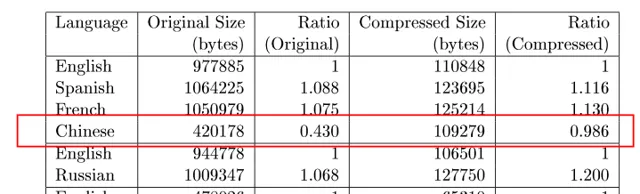
第三个实验中采用了不同文本(欧盟法规),除英语外的所有译文都被扩充了,而中文是其中被扩充最多的。对此研究者的解释是,圣经的文本是非常普遍的词汇,而欧盟法规中包含着很多特殊词汇,从其他语言翻译需要很长的文字扩展。这种现象可能是由于法律文本总是期望采用一些特殊词汇来翻译,这些词汇在日常生活中出现的频率不高,因此显得信息很多。如果将法律文本翻译成普遍的词汇,需要做一些语言扩展。但是依然可以看出,中文是「压缩」效率最低的语言。
从上述三个对比实验结果,可以得到结论,中文是压缩效率最低的语言,或者可以认为是最接近信息熵界限的语言。
虽然这个实验设计的也并不完美,但是从多个实验结果来看和近似估计来看,
中文是英语,西班牙语,法语,中文,汉语,阿拉伯语,日文,俄语这些主流语言中信息熵最大的语言。
如果存在完美的语言,那么应当达到信息压缩下界,但是即使我们知道了信息压缩的下界,怎么达到它又是另外一个非常大的课题。
在找到办法准确计算语言的信息压缩下界之前,类似是否存在/是否可以设计完美语言的这种问题我们都无法回答。
[1] Shannon C E. Prediction and entropy of printed English[J]. Bell system technical journal, 1951, 30(1): 50-64.
[2] Cover T, King R. A convergent gambling estimate of the entropy of English[J]. IEEE Transactions on Information Theory, 1978, 24(4): 413-421.
[3] Wong K, Poon R. A Comment on the Entropy of the Chinese Language[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1976, 24(6): 583-585.
[4] Fromkin V, Rodman R, Hyams N. An introduction to language[M]. Cengage Learning, 2018.
[5] Behr Jr F H, Fossum V, Mitzenmacher M D, et al. Estimating and comparing entropy across written natural languages using PPM compression[J]. 2002.











