想加的太多了，中学生自己挑一个吧：
基础统计学
动机
理解概率和风险不仅对对冲基金经理和扑克玩家至关重要，对每个人的日常生活同样意义重大。事实上，缺乏这种理解正是导致人类认知中一些最基本的逻辑谬误和偏见的根源。
假设某天早上你查看天气预报，看到下雨概率为 50%，这究竟意味着什么？如果你做了一个假阳性率为 2% 的癌症检测，你实际患癌的几率有多大？彩票、个人养老金或房贷的预期收益又是多少？
这些问题对生活中的重大决策都至关重要——从健康到选择就读的大学，无所不包。思考未来就意味着要思考概率，而当今的教育体系在这方面却严重欠缺，未能充分培养学生这方面的能力。
牢固掌握基本的概率和统计学知识，将使学生能够在金钱、健康和未来方面做出明智的决策，同时也能够理解数据呈现的基本原理及其背后的含义。
合格标准
要通过本课程，学生需要参加一次现场考试，以证明他们对以下内容的理解：
频率学派与贝叶斯学派对概率的诠释
示例回答：
频率学派视角：如果天气预报说下雨概率是 10%，那么从长期来看，我每出门 10 次，大约有 1 次会遇到雨。
贝叶斯学派视角：假设某种癌症检测的假阳性率是 2%，而我的检测结果呈阳性。这并不直接意味着我患有癌症，而是表明我患癌症的可能性增加了 50 倍（100/2=50）。要得出在这个新信息下我实际患癌症的概率，我需要将这个倍数与我原本患癌症的基础概率相乘。
复利效应在投资和债务中的体现
示例回答：假设我借了 1,000 元，年利率是 5%。那么一年后，我欠的金额会增加到 1,000 * 1.05 = 1,050 元；再过一年，欠款会进一步增加到 1,050 * 1.05 = 1,102.5 元，以此类推。可以看到，债务金额会以越来越快的速度增长。投资也遵循同样的原理，只是方向是正面的，你的钱会越来越多。
平均值、中位数和众数的区别
示例回答：平均值是所有数据的总和除以数据的个数，容易受极端值的影响。比如，在一个小公司里，如果老板的工资特别高，会大幅拉高整体的平均工资。 中位数是将所有数据从小到大排列后，取中间的那个数，不易受极端值影响。在上述公司的例子中，中位数工资能更好地反映大多数员工的真实收入水平。 众数则是出现次数最多的数值，适合用于数据分布中有明显重复值的情况，比如常见的鞋码或衣服尺码。
正态分布和幂律分布的特征
示例回答：正态分布就像人的身高分布，大多数人的身高都集中在平均水平附近，而极高或极矮的人相对较少。 幂律分布则像是名气的分布，大多数人默默无闻，而极少数人非常出名，形成一个长尾效应。
概率中「与」、「或」和「非」的运用
示例回答：在概率计算中，每增加一个「与」条件，概率就会降低，因为这相当于在韦恩图中取交集，满足条件的范围变小。「或」通常会增加概率，因为它包含了更多的可能性，但要注意不要重复计算重叠部分。（基本上是下面的图，但不需要技术术语。）
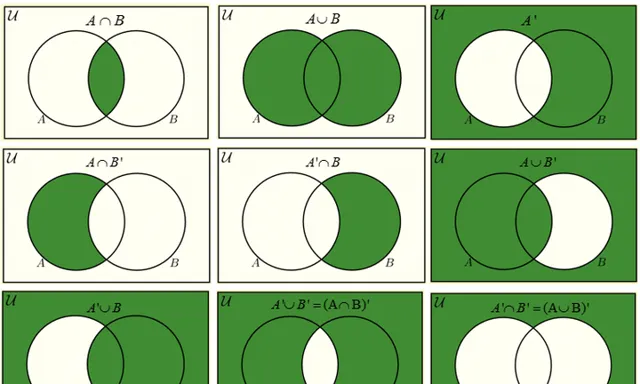期望值的计算及其应用
示例回答：期望值是将某事发生的概率与其价值相乘。例如，一张彩票售价 1 元，中奖概率是百万分之一，奖金是 10 万元。那么这张彩票的期望值是 0.1 元（100,000 * 0.000001 = 0.1）。这意味着，从长期来看，你每花 1 元买彩票，平均只能得到 0.1 元的回报，显然不是一个好的投资。
统计和概率在实际生活中的应用
示例回答：在做人生规划时，可以运用概率思维。比如，考虑成为社交媒体红人这个职业选择。虽然成功后可能收入很高，但实际上能成功的人很少，这是一个典型的幂律分布。如果我们将成功的低概率考虑进去，尽管潜在收益很高，但其期望收益可能并不如我们想象的那么可观。这种思考方式可以帮助我们做出更理性的决策。
基础工业史
动机
历史是一门教学难度极高的学科，设计相关课程更是挑战重重。
历史跨越数千年，涵盖全球各地，而且每个历史时期都可以从多角度、多维度进行解读，这使得历史教学的内容浩如烟海。
然而，由于我们设计的是一门必修课程——即所有学生都必须学习并通过的课程，这在一定程度上简化了课程设计。我们可以将教学内容聚焦于我们认为每个人必须掌握的历史知识。
在当今时代，中国学生并不需要了解罗马帝国或古希腊的历史。事实上，他们甚至不需要深入学习唐朝或宋朝的具体细节——因为这些知识在他们的日常生活中很少派得上用场。
相反，这些学生确实需要理解的是：现代社会与人类历史上的其他时期有何不同，以及造成这种差异的原因。他们需要明白，他们所生活的这个富足时代是如何形成的，以及是什么力量在支撑着我们当前的社会制度和生活方式。
如果不能理解这些关键问题，公民在面对税收、监管和治理等议题时就可能做出错误的选择。这种认知缺失还会导致人们对财富的创造和分配产生严重误解，而这种误解恰恰是人类历史上一些最可怕政权得以兴起的温床。
合格标准
为了通过本课程，学生需要参加一次现场考试，以证明他们对以下内容的理解：
工业革命的核心理念，包括人均可用能源的增加、精密测量技术的应用，以及可互换零件的使用。
示例回答：尽管煤炭的使用对环境造成了负面影响，但它使人类首次能够大规模利用非人力和畜力的能源。结合精密测量技术和可互换零件的概念，人类历史上首次实现了机器的设计、制造和批量生产。
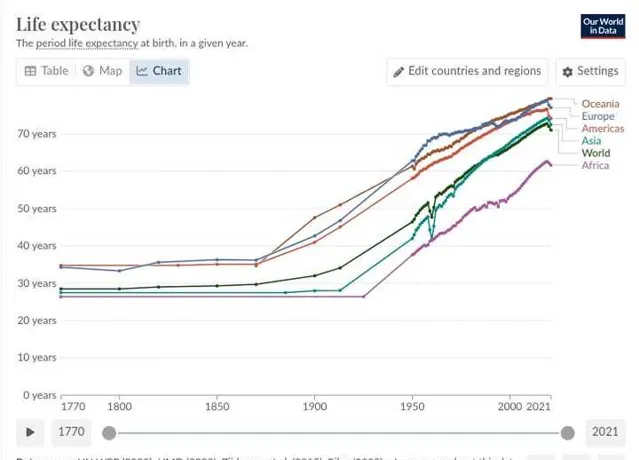
从预期寿命、儿童和母亲死亡率等角度比较工业革命前后的人类生活质量。
示例回答：工业革命之前，社会中只有少数精英掌握着绝大部分财富，而普通民众则生活贫困，寿命短暂。工业革命后，科学和工业的进步显著提高了人类的平均寿命，同时大幅降低了儿童死亡率。
资本主义制度、公司组织形式，以及私有财产制度和政府对权利的保护，如何促进了人与人之间的正和博弈式互动。
示例回答：公司允许多人联合起来，创建能够超越个人能力的组织。资本主义与权利保护使得人们能够投资未来。这些力量的结合，使得人们能够构建未来回报丰厚的事物，通过创造新的财富来源帮助人们积累财富。
人类是如何成功解决过去的重大问题的，例如脊髓灰质炎疫苗的研发、农业绿色革命、哈伯-博世氨合成工艺、臭氧层空洞问题、酸雨治理等
示例回答：你无法像很久以前那样，每英亩地养活很多人。人们开始使用蝙蝠粪便作为肥料，但蝙蝠粪便有限，它们快要用完了。哈伯-博世工艺应运而生，它从大气中提取氨来制造肥料，从而拯救了无数免于饥饿的生命。
从工业革命到摩尔定律，理解进步的指数性质
示例回答：一旦达到一定程度的进展，你就可以利用这些进展取得更大的进步，因此进展会随着时间推移而复合增长。摩尔定律，即利用更快的计算机来制造更快的计算机，就是这一现象的例证。
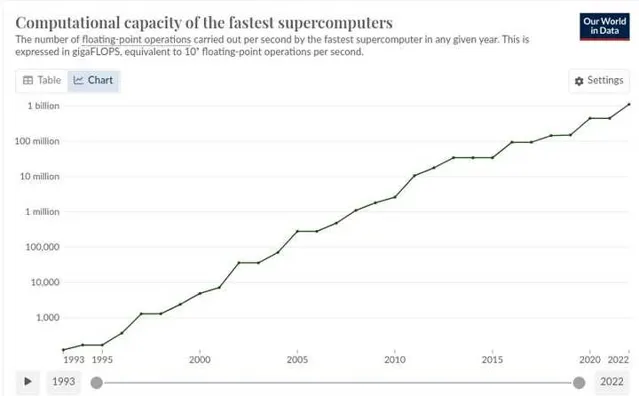人类伟大工程巡礼：从三峡大坝、青藏铁路到南水北调工程和载人航天工程
示例回答：人类真是太棒了！我们创造了许多令人惊叹的杰作，比如三峡大坝，它不仅发电，还防洪、航运，造福无数人。更不可思议的是，我们修建了青藏铁路，这条世界上海拔最高、线路最长的高原铁路，让「世界屋脊」与内地紧密相连！我们甚至实现了载人航天，把中国人的足迹送上了太空！
基础科学
方法论
动机
「科学」一词兼具双重含义：其一是指探索真理的方法论，其二是指通过这种方法论所积累的知识体系。
理解这一方法论是什么、为何与之前的不同，以及如何在生活的各个方面运用它，对于理解人类如何取得如今的成就至关重要。
合格标准
为通过本课程，学生需要参加一次现场考试，展示对以下内容的理解：
科学的核心：理论必须经过实验检验。换言之，认识世界最有效的方法就是与世界直接互动。
示例回答： 你可以在沙发上冥思苦想很久，但若真想了解这个世界，最终还是得亲身去探索和研究。
实验结果如何随现实世界的真相而变化
示例回答： 设计实验时，我们期望能根据现实情况得到不同的结果。例如，要验证不同重量的物体是否以相同速度下落，你可以同时放下两个物体并观察结果；如果它们同时着地，就说明下落速度相同，否则就不同。
当前科学研究的标准流程
示例回答： 科学家们通过收集数据、进行实验，然后运用统计方法分析数据来验证假设。尽管数据解读颇具挑战性，但科学家们会竭尽全力。随后，他们会撰写一篇详细阐述研究过程的论文，提交给同行评审。最终，论文会在学术期刊上发表。
对证据的概率性理解，以及证据与证明之间的区别
示例回答：证据能够增加某事发生的可能性，但这种可能性的增加程度取决于你原本对获得证据的预期。举个例子，如今人人随身携带相机，那么假如大脚怪真的存在，我们理应期望有人能拍到一张清晰的照片。然而事实是，至今没有人拍到，这就成了大脚怪不存在的证据。不过，要注意的是，证据并不等同于证明。证据只是增加或减少某事的可能性，而证明则是确凿无疑的。
为什么预测未来比解释过去更能有效检验知识水平
示例回答： 如果你进行一项实验而未做出预测，那么你大可声称你预料到了所发生的一切，并以此证明你一直是对的。但若你公开做出预测或打赌，那么当你出错时，便无法逃避责任；你必须直面你的信念与事实不符的现实。
相关性与因果关系
示例回答： 假设我们经常发现两件事同时出现，比如财富和教育水平。它们
相关
。这是否意味着一个导致了另一个呢？嗯，存在多种不同的可能性。如果 A 和 B 相关，那么可能性包括：
A 导致 B
B 导致 A
其他因素 C，导致了 A 和 B 的发生
它们同时出现纯属偶然
你必须做实验才能知道哪个是真的。
基础信息素养
动机
人类如今所处的信息环境，与我们在进化过程中所适应的环境有着天壤之别。它与人类历史上绝大多数时期的环境都截然不同。即便与短短二十年前相比，现在的信息环境也已经发生了翻天覆地的变化！
在这样一个环境中游刃有余是一项关键技能，它不仅关乎如何在纷繁复杂的世界中自如行走，更是学习本身的必备条件。我们该如何辨别哪些信息是可信的？如何区分事实与观点？
同时，为孩子们应对社交媒体做好准备也至关重要。虽然我个人更希望避开社交媒体，但我认为，完全禁止使用社交媒体的做法，可能会像过去那种老套的禁欲教育一样收效甚微。
合格标准
要顺利通过本课程，学生需要参加现场考试，证明自己理解了以下内容：
事实与观点
示例回答：事实是确实发生的事情或可验证的客观现实，而观点则是人们对这些事实的
感受
和看法。事实不等同于观点，观点也不等同于事实。
地图不等同于领土
示例回答：人们
相信
的和客观
事实
之间常常存在差异。有时两者一致，有时却大相径庭。每个人的头脑中都有一套关于世界的信念和认知模型，但这些信念和模型可能与现实不符。不同的人面对同一个
领土
（即客观存在的现实世界）时，可能会在头脑中形成不同的
地图
（即对现实的理解和认知）。
媒体更注重娱乐性，而非真实性
示例回答：新闻频道、报纸和其他新闻来源实际上并不会因报道真实、客观的事实而得到奖励或受到惩罚。它们和其他企业一样，首要目标是盈利，因此它们追求的是受众参与度。为了获得更多点击量和点赞，它们可能会不顾真实性发布吸引眼球的内容。这并不意味着媒体总是在撒谎，但也不能保证它们始终在如实报道真相。
社交媒体如何扭曲真相
示例回答：在社交媒体上，人们倾向于只展示自己最好的一面，精心挑选值得炫耀的内容。其他人也是如此。这就意味着，当你看到某人在社交媒体上的生活似乎非常精彩时，你看到的只是他们生活的精华部分，而非完整的现实图景。同样，当你看到许多人似乎比你更成功时，不必感到沮丧或自卑——他们表面上的成功并不意味着你的生活就更糟糕。
如何研究一个主题
示例回答：假设我想了解更多关于某事物的信息，比如苔藓。我可以使用谷歌或其他搜索引擎进行搜索，在维基百科上阅读相关内容，或者向大语言模型询问。交叉验证这些信息来源是个好主意，因为其中某些信息可能存在错误，尤其是在话题具有争议性时。
如何改变自己的想法
示例回答：随着你获取更多信息，改变对事物的看法是很自然的。这很好！你应当始终保持开放心态，因为总有可能你之前的看法是错误的。如果你从不改变想法，那么你对新信息毫无反应——这意味着你可能更像一块石头，而非一个活生生的人。人会变，石头不会。
基础经济学
动机
我远非经济学专家，但我可以告诉你什么是供需，以及它们为何重要。我可以谈论供需的弹性，以及它通常如何决定税收负担的归属。我可以告诉你价格上限和下限对市场的影响。
我可以告诉你市场为何运作，以及为何这至关重要。
这不应该是某种精英知识。它不应该隐藏在大学课程背后。这实际上是我们整个经济运作的框架。
这应该在每所学校教给每个孩子。
课程将围绕此图展开：
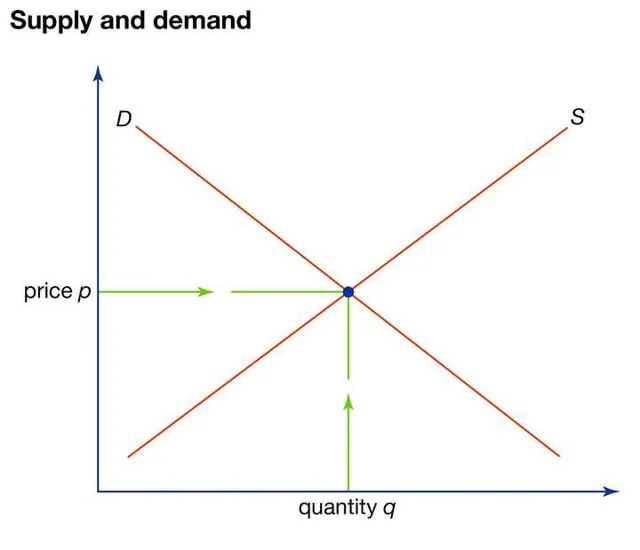
目前已有众多基础经济学课程，因此将这些课程调整到适合第 2 阶段学生（大约 10-13 岁）的水平应该不会太困难。需要注意的是，学生的入学并不严格按照年龄划分——如果他们需要更大的年龄才能理解这些概念，那也无妨。课程不需要涉及太多数学知识——实际上，除了理解上面的图表外，几乎不需要用到任何数学。
合格标准
为了通过这门课程，学生需要参加一次现场考试，展示对以下内容的理解：
供给、需求与价格均衡
示例回答：供给和需求反映了某种商品或服务在不同价格水平下的交易数量。商品的实际价格和生产数量由供需曲线的交点决定，即供给等于需求的均衡点。
供给和需求曲线斜率的成因
示例回答：供给曲线：随着生产规模扩大，边际成本上升，因此价格上涨。需求曲线：商品价格上涨时，需求量减少；价格下降时，需求量增加。
供给和需求弹性的含义
示例回答：弹性衡量的是对价格变化的敏感程度。需求弹性：对于非必需品，如电影票，价格上涨会导致需求显著下降。但对于必需品，如住房，即使价格上涨，需求变化也相对较小。供给弹性：取决于增加一单位产量的边际成本。例如，新建一栋房屋成本高昂，供给弹性低；而复制一份视频游戏成本很低，供给弹性高。
价格下限和上限的影响
示例回答：价格下限是某物可以出售的最低价格，高于没有下限时的价格。这就像最低工资，会导致供过于求，因为供应量大于需求量。价格上限是某物可以出售的最高价格，低于没有上限时的价格。这就像租金管制，会导致短缺，因为需求量固定在高于供应量的水平。
税收负担所在及其影响
示例回答：税收落在那些无法逃避它们的人身上。如果所有商品在销售时都被征税，比如销售税，那么人们只需支付更高的价格，税收就落在消费者身上。另一方面，如果只有一家公司被征税，他们就必须支付，因为如果不支付，他们的商品会变得更贵，人们就不会再购买了。一般来说，你征税的东西会减少，因为它使商品变得更贵，减少了人们做事情的动机。
为何市场胜过中央计划
示例回答：市场通过每个人每天各自了解的零碎知识来协调所有人。无论中央计划者多么聪明，他们都不可能比所有人加起来更聪明，也不可能知道其他人所掌握的具体信息。
市场在哪里会失灵
示例回答：市场失灵发生在未将外部性计入价格时，例如公司可以随意向河流倾倒废物。这时政府介入，强制企业将外部性纳入价格考量。这就是公地悲剧。
以上内容节选自：
